【算法】遞歸算法的深度實踐：從布爾運算到二叉樹剪枝的DFS之旅詳情 - C語言,算法,遞歸,深度優先搜索,C,C++,後端開發,yyds乾貨盤點蒙奇D索隆博客

(深度優先遍歷)

遞歸算法

導讀

大家好，很高興又和大家見面啦！！！在上一篇中，我們探討了如何利用深度優先搜索（DFS）的中序遍歷特性，在二叉搜索樹中高效地查找第K小的元素。我們看到了 DFS 如何通過遞歸自然地深入樹的分支，系統地訪問每個節點。 DFS 的核心思想在於“一路到底，再逐步回溯”。這種策略在解決樹形結構的問題時尤為強大。今天，我們將繼續深入這一主題，通過兩道經典的二叉樹問題，進一步鞏固 DFS 的理解與應用，特別關注其 後序遍歷形式 的強大威力。現在，讓我們進入正文，一起探索 DFS 的實踐魅力。

一、2331. 計算布爾二叉樹的值

1.1 題目介紹

題目標籤：樹、深度優先搜索、二叉樹、第82場雙週賽 題目難度：簡單 題目描述：給你一棵完整二叉樹的根，這棵樹有以下特徵：

葉子節點要麼值為 0 要麼值為 1 ，其中 0 表示 False ，1 表示 True 。
非葉子節點要麼值為 2 要麼值為 3 ，其中 2 表示邏輯或 OR ，3 表示邏輯與 AND 。

計算一個節點的值方式如下：

如果節點是個葉子節點，那麼節點的值為它本身，即 True 或者 False 。
否則，計算兩個孩子的節點值，然後將該節點的運算符對兩個孩子值進行運算。

返回根節點 root 的布爾運算值。 完整二叉樹 是每個節點有 0 個或者 2 個孩子的二叉樹。 葉子節點 是沒有孩子的節點。 示例 1：輸入：root = [2, 1, 3, null, null, 0, 1] 輸出：true

flowchart TB
a[2<br>or]
b[1]
c[3<br>and]
d[0]
e[1]
a--->b
a--->c
c--->d
c--->e

解釋：ret = 1 or (0 and 1) = true。 AND 與運算節點的值為 False AND True = False 。 OR 運算節點的值為 True OR False = True 。根節點的值為 True ，所以我們返回 true 。

示例 2：輸入：root = [0] 輸出：false

flowchart TB
a[0]

解釋：ret = 0

根節點是葉子節點，且值為 false，所以我們返回 false 。提示：樹中節點數目在 [1, 1000] 之間。 $0 \leq Node.val \leq 3$ 每個節點的孩子數為 0 或 2 。葉子節點的值為 0 或 1 。非葉子節點的值為 2 或 3 。

1.2 解題思路

該題比較簡單，其結果主要由三部分構成：

左子樹：值為 1 或者 0
根節點：運算符為 or 或者 and
右子樹：值為 1 或者 0

因此整棵樹的值，我們只需要依次計算出左子樹和右子樹後，在將二者通過根節點的運算符完成運算即可；而這個二叉樹的左右子樹均可以通過將其分解為三部分，即，樹中的每棵子樹的值均是由：

左子樹的值
根節點的運算符
右子樹的值

這三部分構成。這種 分而治之 的分解思想正是遞歸的算法思想，而遞歸在 數據結構 中的應用正是 深度優先搜索 算法。在前面我們介紹過，二叉樹 的 中序遍歷 正是 DFS 的表現形式，但是這並不意味着 中序遍歷 就是二叉樹中的 DFS 。對於二叉樹中的 深度優先搜索 ，我們應該理解為：

深度優先 策略在 二叉樹 中的應用

而該應用在 二叉樹 中有三種表現形式：

先序
中序
後序

因此不管是哪種表現形式，我們均可以將其稱為 二叉樹 中的 深度優先 策略。當該策略 + 搜索目的後，就得到了 二叉樹 中的 深度優先搜索；在本題中，我們要想獲得一棵樹的布爾值，我們就需要先獲取左右子樹的值，在通過根節點將二者進行運算，因此該二叉樹的遍歷順序為：

$左子樹 \rightarrow 右子樹 \rightarrow 根結點$

該遍歷順序對應的正是 二叉樹 中的 後序遍歷，也就是説我們要解決本題的具體方式為：

使用 深度優先策略 以後序的形式對該 二叉樹 進行遍歷獲取 二叉樹 的布爾值

1.3 代碼編寫

明確了具體的解題思路後，接下來我們就需要開始編寫相應的代碼了。

1.3.1 定義函數

該函數的目的是：

通過 深度優先 策略對該 二叉樹 以後序的形式完成遍歷獲取樹的布爾值；

因此我們可以採用多種命名方式：

DFT —— 深度優先搜索
DFS —— 深度優先遍歷
Post_Order —— 後序遍歷

這裏我們還是使用 DFS 作為函數名，函數的返回類型為 bool ，函數的參數為樹的根節點 root：

bool dfs(struct TreeNode* root) {
	
}

1.3.2 遞歸基

在樹中，都是以判斷樹是否為空作為遞歸基，在這題中，我們則可以通過各結點的值作為函數的遞歸基：

	if (root->val == 1) {
		return true;
	}
	if (root->val == 0) {
		return false;
	}
	if (root->val == 2) {
		return left || right;
	}
	return left && right;

當結點的值為 0 表示該結點為葉子結點，且對應的值為 false；當結點的值為 1 表示該結點為葉子結點，且對應的值為 true；當結點的值為 2 表示該節點為非葉子結點，且對應的值為 left || right；當結點的值為 3 表示該節點為非葉子結點，且對應的值為 left && right；

1.3.3 遞進關係

在二叉樹中，其遞進關係就是該棵樹的左右子樹：

	bool left = dfs(root->left);
	bool right = dfs(root->right);

1.3.4 組合優化

當我們將上述內容進行整合，就得到了最終的代碼：

bool dfs(struct TreeNode* root) {
	if (root->val == 1) {
		return true;
	}
	if (root->val == 0) {
		return false;
	}
	bool left = dfs(root->left);
	bool right = dfs(root->right);
	if (root->val == 2) {
		return left || right;
	}
	return left && right;
}

bool evaluateTree(struct TreeNode* root) {
	return dfs(root);
}

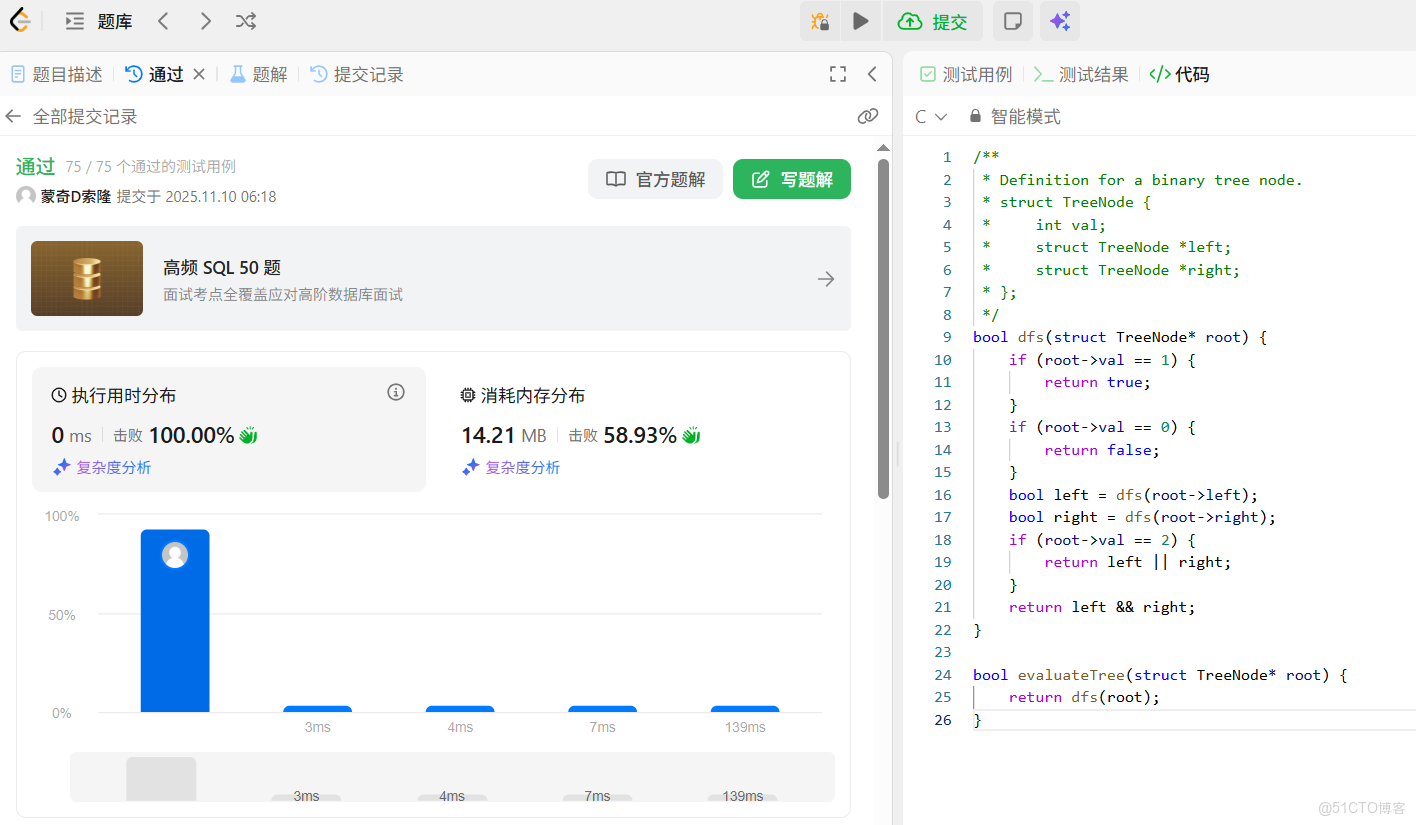
1.4 代碼測試

下面我們就在 leetcode 中對該代碼進行測試：

代碼測試1.png

二、814. 二叉樹剪枝

2.1 題目介紹

題目標籤：樹、深度優先搜索、二叉樹 題目難度：中等 題目描述：給你二叉樹的根結點 root ，此外樹的每個結點的值要麼是 0 ，要麼是 1。返回移除了所有不包含 1 的子樹的原二叉樹。節點 node 的子樹為 node 本身加上所有 node 的後代。 示例 1：輸入：root = [1, null, 0, 0, 1] 輸出：[1, null, 0, null, 1]

flowchart LR
	subgraph t[原樹]
		direction TB
		a((1))
		a--->a1((NULL))
		b((0))
		a--->b
		c((0))
		d((1))
		b--->c
		b--->d
	end

	subgraph T[剪枝後]
		direction TB
		A((1))
		A--->A1((NULL))
		B((0))
		A--->B
		C((NULL))
		D((1))
		B--->C
		B--->D
	end

t--->T
classDef red fill: #ff9999, color: #000, stroke: #ff0000, stroke-width: 2px
class c red
class C red

解釋：只有紅色節點滿足條件“所有不包含 1 的子樹”。右圖為返回的答案。 示例 2：輸入：root = [1, 0, 1, 0, 0, 0, 1] 輸出：[1, null, 1, null, 1]

flowchart LR
	subgraph t[原樹]
		direction TB
		a((1))
		b((0))
		c((1))
		a--->b
		a--->c
		e((0))
		f((0))
		b--->e
		b--->f
		g((0))
		h((1))
		c--->g
		c--->h
	end

	subgraph T[剪枝後]
		direction TB
		A((1))
		B((NULL))
		C((1))
		A--->B
		A--->C
		
		G((NULL))
		H((1))
		C--->G
		C--->H
	end

t--->T

classDef red fill: #ff9999, color: #000, stroke: #ff0000, stroke-width: 2px
class b red
class e red
class f red
class g red
class B red
class G red

示例 3：輸入：root = [1, 1, 0, 1, 1, 0, 1, 0] 輸出：[1, 1, 0, 1, 1, null, 1]

flowchart LR
	subgraph t[原樹]
		direction TB
		a((1))
		b((1))
		c((0))
		a--->b
		a--->c
		d((1))
		e((1))
		b--->d
		b--->e
		f((0))
		g((1))
		c--->f
		c--->g
		h((0))
		d--->h
	end

	subgraph T[剪枝後]
		direction TB
		A((1))
		B((1))
		C((0))
		A--->B
		A--->C
		D((1))
		E((1))
		B--->D
		B--->E
		F((NULL))
		G((1))
		C--->F
		C--->G
		
	end

t--->T

classDef red fill: #ff9999, color: #000, stroke: #ff0000, stroke-width: 2px

class f red
class h red
class F red

提示：樹中節點的數目在範圍 [1, 200] 內 Node.val 為 0 或 1

2.2 解題思路

該題的解題思路很簡單，我們判斷一棵子樹是否需要被剪枝，我們只需要判斷其左右子樹以及根結點中是否存在 1 ：

存在，則不進行剪枝
不存在，則進行剪枝

因此，我們在決定是否要進行剪枝操作前，我們需要先檢查該子樹的左右子樹，具體的操作算法，我們可以通過 深度優先 策略，並以後序的形式對該棵樹進行遍歷；

2.3 代碼編寫

2.3.1 函數定義

該函數的目的為：

通過 深度優先 策略，並以後序的形式對該棵樹進行遍歷

而遍歷的目的是為了判斷是否執行剪枝操作：

樹中存在 1 則不執行任何操作
樹中不存在 1 則執行剪枝操作

因此函數的返回類型為 bool：

bool DFS(struct TreeNode* root) {

}

2.3.2 遞歸基

在該函數中，我們需要根據左右子樹以及根節點來判斷是否需要進行剪枝：

	if (root == NULL) {
		return true;
	}

	if (left && right && root->val == 0) {
		return true;
	}
	return false;

當該樹為空樹時，則表示該結點需要進行剪枝，即返回 true；當樹為非空樹，且其左右子樹均為需要剪枝，且該結點的值為 0 ，則表示該結點需要進行剪枝，即返回 true；當樹為非空樹，且該結點的值為 1 ，則表示該結點不需要進行剪枝，即返回 false；

2.3.3 遞進關係

在二叉樹中，其遞進關係為其左右子樹：

	bool left = DFS(root->left);
	bool right = DFS(root->right);

2.3.4 組合優化

當我們將上面的內容進行整合，並加入剪枝操作後，即可得到完整的代碼：

bool DFS(struct TreeNode** root) {
	if (*root == NULL) {
		return true;
	}
	bool left = DFS(&((*root)->left));
	bool right = DFS(&((*root)->right));
	if (left && right && (*root)->val == 0) {
		free(*root);
		*root = NULL;
		return true;
	}
	return false;
}
struct TreeNode* pruneTree(struct TreeNode* root) {
	bool ret = DFS(&root);
	return root;
}

需要注意的是，由於剪枝操作是直接更改相應的二叉樹，因此我們需要以指針的形式進行傳參；

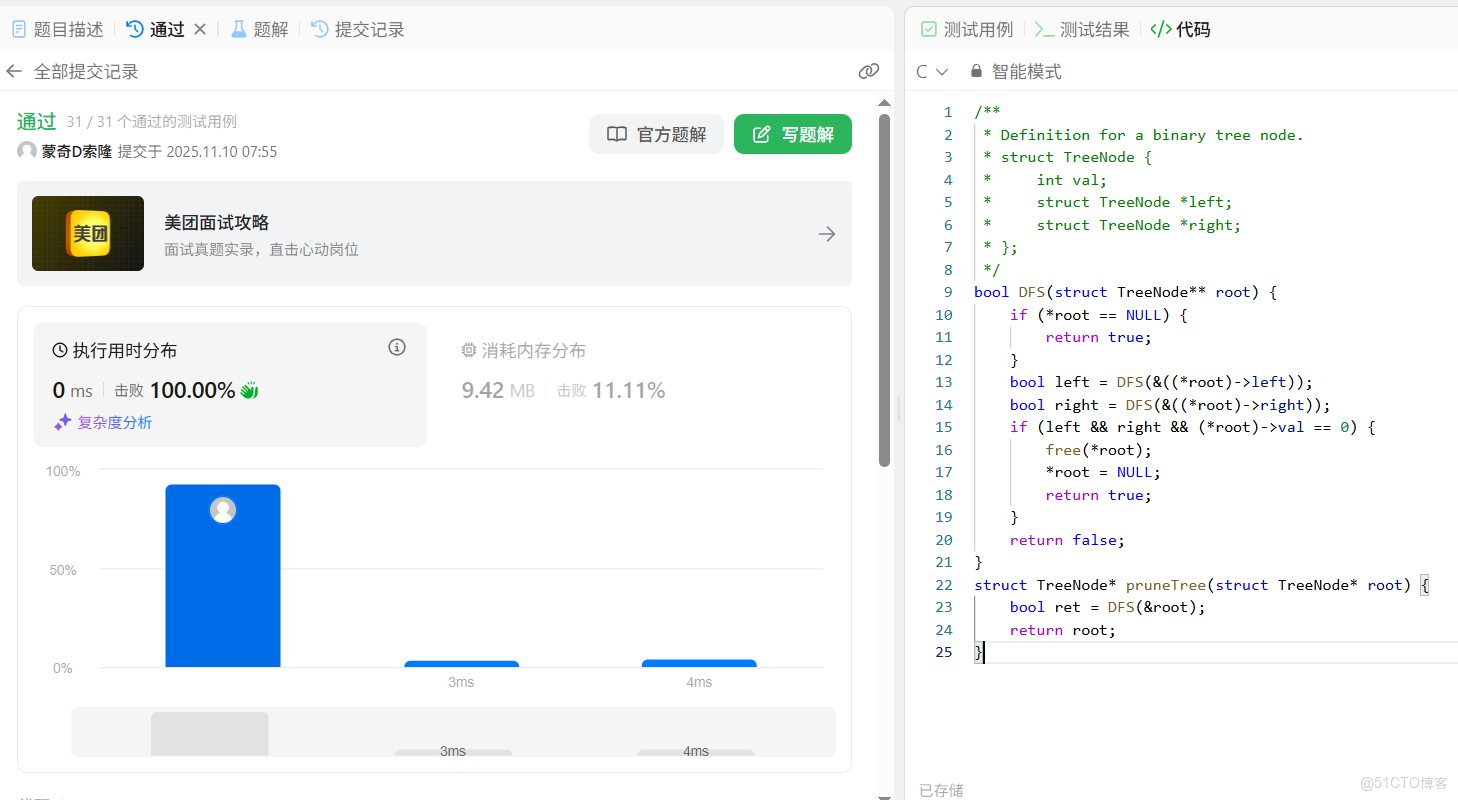
2.4 代碼測試

接下來我們就來測試一下該代碼：

代碼測試2.png

結語

通過今天對兩道 LeetCode 真題的深入剖析，我們進一步鞏固了深度優先遍歷（DFS）在二叉樹問題中的應用。從 2331.計算布爾二叉樹的值 到 814.二叉樹剪枝，我們看到了 DFS後序遍歷 模式的強大威力。 關鍵收穫總結：

問題分解思維：無論是布爾運算還是剪枝判斷，都能通過遞歸自然分解為子問題
後序遍歷的精髓：先處理子樹，再根據子樹結果決定當前節點操作——這正是"自底向上"的解決思路
實踐出真知：通過具體編碼，我們加深了對遞歸基、遞推關係的理解

DFS的學習路徑建議：

掌握三種遍歷方式（前序、中序、後序）的適用場景
理解遞歸在樹結構中的自然應用
通過不同難度題目逐步提升應用能力

深度優先遍歷作為基礎算法思想，其應用遠不止於二叉樹。掌握好這一利器，將為後續學習圖論等更復雜的數據結構打下堅實基礎。 互動與分享

點贊👍 - 您的認可是我持續創作的最大動力
收藏⭐ - 方便隨時回顧這些重要的基礎概念
轉發↗️ - 分享給更多可能需要的朋友
評論💬 - 歡迎留下您的寶貴意見或想討論的話題

感謝您的耐心閲讀！關注博主，不錯過更多技術乾貨。我們下一篇再見！

蒙奇D索隆博客

蒙奇D索隆博客

博客 / 詳情