(深度優先搜索)

導讀

大家好，很高興又和大家見面啦！！！   在前面的內容中，我們共同探索了漢諾塔的奧秘，體驗了快速冪算法的高效，感受到了遞歸思維解決複雜問題的獨特魅力。今天，我們將沿着遞歸這條主線繼續前行，探索它在數據結構中的一個重要應用場景。   遞歸不僅僅是一種編程技巧，更是一種解決問題的思維方式。當我們掌握了遞歸的基本原理後，很自然地會想知道：這個強大的工具在樹、圖這樣的複雜數據結構中能發揮怎樣的作用？   這正是深度優先搜索（DFS）要帶給我們的答案——它完美展現了遞歸思維如何優雅地解決數據結構中的遍歷與搜索問題。從基本概念的釐清到實際問題的解決，DFS都體現了遞歸思想的精髓。   現在，就讓我們開始這次探索之旅，看看遞歸思維如何在數據結構中綻放光彩。

一、基本概念

1.1 遍歷

• 基本定義：遍歷​ （Traversal）是一種算法過程，指的是按照某種規則，系統地訪問數據結構（如數組、鏈表、樹、圖）中的每一個節點（元素）一次且僅一次的過程。

• 目的：其核心目的是“訪問全部”，確保不重不漏。訪問時執行什麼操作（如打印、修改）是另一個層面的問題。

• 基礎性：遍歷是更高級操作（如搜索、計算路徑）的基礎。

1.2 深度優先遍歷

• 基本定義：深度優先遍歷（Depth-First Traversal, DFT）是遍歷樹或圖的一種策略。

  • 核心思想：儘可能深地探索分支路徑，當一條路徑走到盡頭（即遇到葉子節點或已訪問過的節點）時，再回溯到上一個分叉點，選擇另一條未探索的路徑繼續深入。

• 核心要點：

  • 順序：遵循“後進先出（LIFO）”的原則，通常使用 棧 這種數據結構（顯式使用或通過 遞歸 調用隱式使用）來實現。

  • 結果：深度優先遍歷會產生特定的序列。

    • 在樹結構中，有前序、中序、後序遍歷。
    • 在圖中，根據選擇的路徑不同，其 DFT 的遍歷序列也有所不同

1.3 廣度優先遍歷

• 基本定義：廣度優先遍歷（Breadth-First Traversal, BFT）是遍歷樹或圖的另一種策略。

  • 核心思想：從起點開始，先訪問所有相鄰的節點，然後再訪問這些相鄰節點的相鄰節點，以此類推，一層一層地向外擴展。

• 核心要點：

  • 順序：遵循“先進先出（FIFO）”的原則，必須使用 隊列 這種數據結構來實現。

  • 特性：它保證在訪問第 $n+1$ 層的節點之前，第 $n$ 層的所有節點都已被訪問。因此，它常被用於尋找最短路徑（在邊權為1的圖中）。

1.4 搜索

• 基本定義：搜索（** Search**）是一種算法過程，其目標是在一個數據集合或問題空間中，尋找一個滿足特定條件的目標元素（解）。

• 核心要點：

  • 目的性強：搜索 是目標導向的，一旦找到目標，過程就可以終止。

  • 與遍歷的關係：搜索通常是基於某種遍歷策略實現。你可以把搜索理解為一種“帶有提前終止條件的遍歷”。

1.5 暴力搜索

• 基本定義：暴力搜索（** Brute-Force Search**）又稱窮舉搜索，是一種最簡單直接的搜索策略。它系統地枚舉所有可能的候選解，並逐一檢查其是否滿足問題的條件。

• 核心要點：

  • 全面性：只要時間允許，它保證能找到解（如果解存在的話）。

  • 低效性：其時間複雜度通常非常高，是指數級的，因此只適用於問題規模很小的情況。

  • 與遍歷的關係：暴力搜索通常意味着對整個問題空間進行一種“無差別”的遍歷。

1.6 深度優先搜索

• 基本定義：深度優先搜索（Depth-First Search，DFS）是一種利用深度優先遍歷策略來實現的搜索算法。

  • 搜索過程：它在搜索時，會沿着一條路徑儘可能深地探索，直到找到目標或走到盡頭，然後回溯。

• 核心要點：

  • 它繼承了深度優先遍歷的所有特性（使用 棧/遞歸 ）。

  • 常用於需要搜索整個解空間的問題，如拓撲排序、檢測圖中環、解決迷宮問題等。

• 與深度優先遍歷的區別：

  • 深度優先遍歷：強調過程，目的是訪問所有節點。

  • 深度優先搜索：強調目標，目的是找到特定節點或解，它可能在過程中途就提前結束。

1.7 廣度優先搜索

• 基本定義：廣度優先搜索（Breadth-First Search, BFS）是一種利用廣度優先遍歷策略來實現的搜索算法。

  • 搜索過程：它在搜索時，會從起點開始，按距離起點的層次由近及遠地進行探索。

• 核心要點：

  • 它繼承了廣度優先遍歷的所有特性（使用 隊列 ）。

  • 當圖中的邊沒有權重（或權重相等）時，BFS 找到的路徑一定是最短路徑。因此它被廣泛應用於最短路徑問題、社交網絡中查找最短關係鏈等。

• 與廣度優先遍歷的區別：

  • 廣度優先遍歷：強調過程，目的是訪問所有節點。

  • 廣度優先搜索：強調目標，目的是找到特定節點或解，它可能在過程中途就提前結束。

1.8 總結關係

這些概念可以看作一個清晰的層次結構：

1. 遍歷 $VS$ 搜索：這是最高層的區分。遍歷是手段（訪問全部），搜索是目的（尋找特定目標）。搜索通常通過遍歷來實現。

2. 兩種策略：深度優先和廣度優先是兩種核心的策略，它們既可以用於“遍歷”，也可以用於“搜索”。

3. 具體實現：

   • 深度優先策略 + 遍歷目的 = 深度優先遍歷

   • 深度優先策略 + 搜索目的 = 深度優先搜索

   • 廣度優先策略 + 遍歷目的 = 廣度優先遍歷

   • 廣度優先策略 + 搜索目的 = 廣度優先搜索

4. 暴力搜索是一個更上位的概念，它描述了“枚舉所有可能”的思想，而 DFS 和 BFS 是實現在圖等結構上暴力搜索的兩種具體、系統化的方法。

二、具體實現

深度優先搜索 就是遞歸算法在 數據結構 中的實際應用，常被用於 樹 與 圖 這兩種數據結構中。這裏我們以 樹 為例來説明該算法的具體實現；

2.1 樹中的深度優先搜索

深度優先搜索 的特性是 LIFO，該特性與樹中的中序遍歷一致，也就是説當我們在對樹進行帶有特定條件的中序遍歷時，我們就是在對該棵樹進行 深度優先搜索。   通常我們會以該算法的縮寫——DFS 來表示該算法，因此在接下來的實現中，該算法的具體實現對應的函數名我們選擇使用 DFS 或者 dfs

2.2 函數定義

函數的定義主要是定義函數的三要素——函數名、函數參數、函數的返回類型：

• 函數名——當前我們實現的函數功能為：深度優先搜索，因此函數名我們選擇 dfs；

• 函數參數——該還是主要用於對 樹 進行 深度優先搜索，因此函數參數有兩個：

  • root ：樹的根節點
  • x ：需要在樹中查找的特定值

• 函數的返回類型——該函數是用於查找特定值是否存在於樹中，因此函數的放回類型我們有多種選擇：

  • bool —— 只用於簡單的查找該值是否存在於樹中
    • 存在則返回 true
    • 不存在則返回 false
  • TreeNodeType* —— 用於找到該值的具體位置
    • 存在則返回該值所在結點的地址
    • 不存在則返回 NULL

2.3 遞歸基

樹 本身就是一種 遞歸型 的數據結構，因此在對該數據結構進行各種操作時，均可通過 遞歸 實現。   在 樹 中，各種操作是否能夠執行，取決於當前訪問的樹是否為空樹，因此在 樹 中，其遞歸基可以直接通過判斷該樹是否為空樹：

	if (root == NULL) {
		return NULL;
	}

2.4 遞進關係

樹 作為一種 遞歸型 的數據結構，其遞進關係就是該棵樹的子樹，這裏我們以 二叉樹 為例：

	BTNode* p = dfs(root->lchild, x);
	if (p == NULL) {
		p = dfs(root->rchild, x);
	}
	return p;

2.5 組合優化

接下來我們將上述內容組合在一起，就得到了 二叉樹 中的 dfs：

BTNode* dfs(BTree root, ElemType x) {
	if (root == NULL) {
		return NULL;
	}
	BTNode* p = dfs(root->lchild, x);
	if (p == NULL) {
		p = dfs(root->rchild, x);
	}
	return p;
}

三、230. 二叉搜索樹中第 K 小的元素

3.1 題目介紹

題目標籤：樹、深度優先搜索、二叉樹、二叉搜索樹 題目難度：中等 題目描述： 給定一個二叉搜索樹的根節點 root ，和一個整數 k ，請你設計一個算法查找其中第 k 小的元素（從 1 開始計數）。

示例 1： 輸入：root = [3, 1, 4, null, 2], k = 1 輸出：1

示例 2： 輸入：root = [5, 3, 6, 2, 4, null, null, 1], k = 3 輸出：3

提示：

樹中的節點數為 $n$ 。 $1 \leq k \leq n \leq 10^4$ $0 \leq Node.val \leq 10^4$

進階：如果二叉搜索樹經常被修改（插入 / 刪除操作）並且你需要頻繁地查找第 k 小的值，你將如何優化算法？

3.2 解題思路

常規的思路我們可以通過一個數組，將樹中的元素從小到大依次進行存儲，之後再返回下標為 k -1 的元素即可；   在該思路中，數組的大小取決於樹中的結點數量，而該數量我們可以通過中序遍歷的方式獲取：

int Get_Size(TN* root) {
	if (root == NULL) {
		return 0;
	}
	int left = Get_KSize(root->left);
	int right = Get_KSize(root->right);
	return left + right + 1;
}

但是該思路在經常被修改的二叉搜索樹中，則不再適用，因為當二叉樹被修改時，其對應的數組大小也將被頻繁修改，所以會大大降低算法的效率；   這題我們將會採取一種更優的算法思路——直接通過 dfs 實現查找；   在 BST 中，樹中的各結點滿足 $左子樹 < 根節點 < 右子樹$ ，因此當我們要查找較小值時，我們只需查找左子樹；當我們要查找較大值時，我們只需查找右子樹；   以下面這棵二叉搜索樹為例：

flowchart TB
a((20))
b((10))
c((30))
a--->b
a--->c

d((6))
e((17))
b--->d
b--->e

f((4))
g((7))
d--->f
d--->g

h((13))
i((19))
e--->h
e--->i

我們需要找到該 BST 中第 k 個最小的數，這是我們需要通過 dfs 從左子樹中開始查找；   通過 dfs 我們找到的該樹中最小值為樹中的最左側結點 4 ，此時我們可以開始進行計數；

flowchart TB
a((20<br>count = 8))
b((10<br>count = 4))
c((30<br>count = 9))
a--->b
a--->c

d((6<br>count = 2))
e((17<br>count = 6))
b--->d
b--->e

f((4<br>count = 1))
g((7<br>count = 3))
d--->f
d--->g

h((13<br>count = 5))
i((19<br>count = 7))
e--->h
e--->i

若我們只是對該 BST 進行遍歷操作，那麼每個結點對應的計數如上圖所示。可以看到，每個結點對應的計數值，正是該結點按由小到大順序排列時的位置；   因此我們的思路就是對該二叉樹進行一次 dfs ，找到 count == k 的結點，該結點即為我們需要獲取的第 k 小的元素。

3.3 代碼編寫

3.3.1 函數定義

該思路的實現是對該 BST 進行一次 dfs ，因此我們直接以 DFS 作為其函數名；   函數的參數有三個：

• root —— 遍歷樹的根結點
• k —— 計數變量
• ans —— 返回值變量

該函數只需要對 BST 進行一次 dfs ，因此函數不需要任何返回值，即，該函數的返回值為 void

3.3.2 遞歸基

在該算法中，控制算法的因素有兩個：

• root —— 當樹為空樹時，結束遍歷
• k —— 當找到目標 k 時，結束遍歷

這裏需要注意的是，若我們直接使用題目所給的變量 k ，那麼則可以通過 k 的自減，來對各個結點進行編號，此時，我們需要尋找的目標值就變成了 k == 0 的值；   這裏我們還是以上面介紹的 BST 為例，當 k == 6 時，那麼樹中的各個結點對應的編號為：

flowchart TB
a((20<br>count = -2))
b((10<br>count = 2))
c((30<br>count = -3))
a--->b
a--->c

d((6<br>count = 4))
e((17<br>count = 0))
b--->d
b--->e

f((4<br>count = 5))
g((7<br>count = 3))
d--->f
d--->g

h((13<br>count = 1))
i((19<br>count = -1))
e--->h
e--->i

每完成一次結點的訪問，就需要對 k 值進行一次自減操作，因此，每個結點對應的 k 值與上圖中展示的 count 值一致，結點的對應編號會從 k - 1 開始進行遞減編號；   所以當找到編號為 0 的結點是，該節點中存儲的值就是我們需要尋找的目標值；   因此 k == 0 也是控制該算法結束的一個條件：

	if (root == NULL || k == 0) {
		return;
	}

3.3.3 遞進關係

在 二叉樹 中，其 dfs 實質上就是對該樹進行 中序遍歷，而 中序遍歷 的順序為：$左子樹 \rightarrow 根結點 \rightarrow 右子樹$，即：

	DFS(root->left, k, ans);
	*k -= 1;
	if (*k == 0) {
		*ans = root->val;
	}
	DFS(root->right, k, ans);

在對根結點的訪問中，我們只需要對該結點進行一次編號即可，而這裏對 k 值的判斷，實際上做的就是記錄 k == 0 時，結點中存儲的數值。   當然我們也可以將訪問根結點的操作給封裝成函數 visited ，這裏我就不進行展開了，感興趣的朋友可以關注一下 【數據結構】專欄，其中介紹 二叉樹 的遍歷操作時，有進行詳細介紹。

3.3.4 組合優化

接下來我們只需要將前面的內容進行整合即可：

void DFS(TN* root, int* k, int* ans) {
	if (root == NULL || k == 0) {
		return;
	}
	DFS(root->left, k, ans);
	*k -= 1;
	if (*k == 0) {
		*ans = root->val;
	}
	DFS(root->right, k, ans);
}
int kthSmallest(struct TreeNode* root, int k) {
	int ans = 0;
	DFS(root, &k, &ans);
	return ans;
}

這裏需要注意，因為我們需要改變 k 與 ans 的值，因此我們需要在傳參時，傳入這兩個變量的地址，並且在 DFS 中，通過指針來修改其值；

3.4 代碼測試

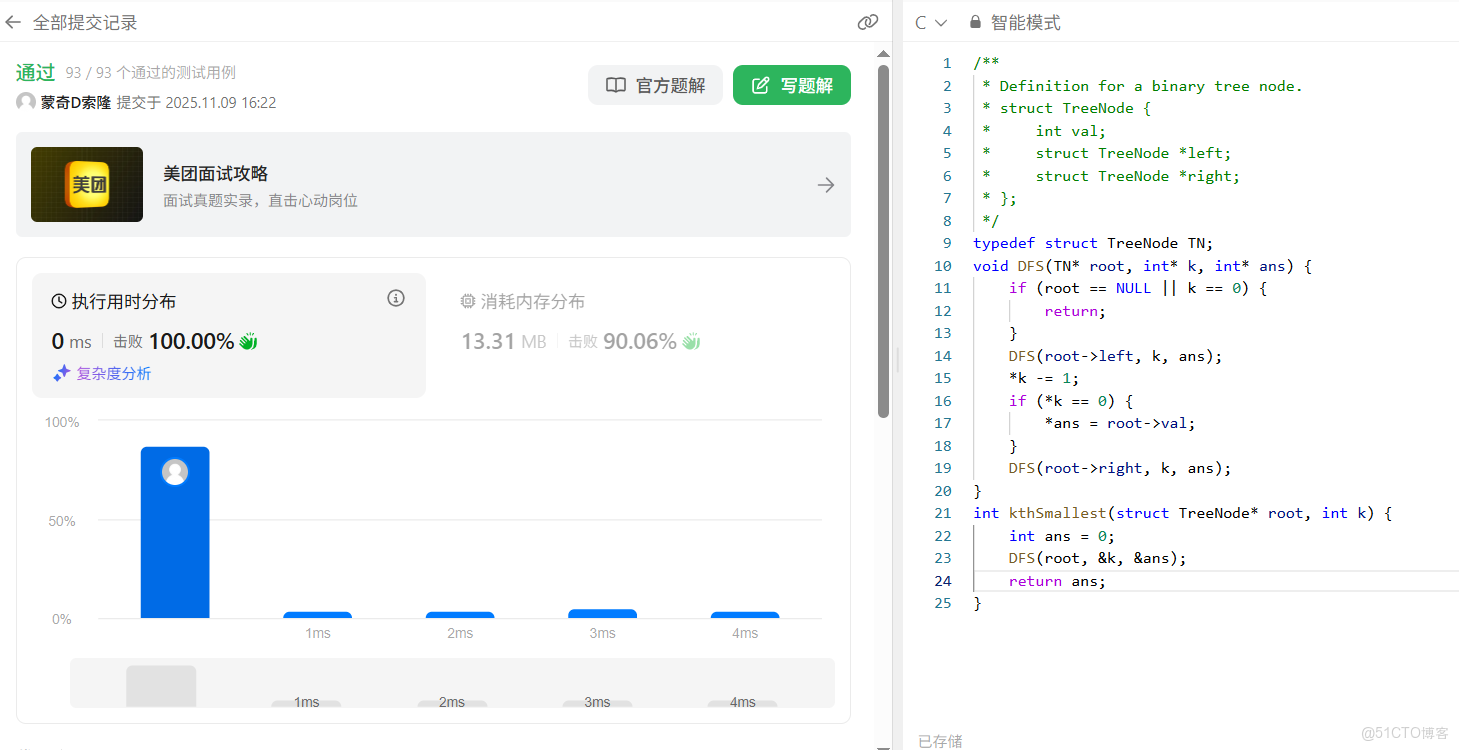
下面我們就在 leetcode 中對該算法進行測試：

可以看到，此時我們很好的通過 DFS 算法解決了該問題；

結語

通過本文的系統學習，我們共同完成了對深度優先搜索（DFS）算法的完整探索。從理論概念到代碼實現，再到實戰應用，相信您已經對 DFS 建立了全面的認識。   核心要點回顧

• 概念層面：清晰區分了遍歷與搜索的本質差異，明確了 DFS 與 BFS 的適用場景

• 實現層面：深入理解了 DFS 的遞歸實現機制，掌握了在樹結構中的具體應用

• 實戰層面：通過LeetCode 230題的分析，展示了 DFS 解決實際問題的完整流程

知識拓展建議

• 基礎鞏固：嘗試用 DFS 解決二叉樹的其他問題，如路徑總和、最大深度計算等

• 進階提升：探索 DFS 在圖結構中的應用，如連通分量識別、拓撲排序等

• 優化思考：研究剪枝策略在 DFS 中的應用，提升算法效率

DFS 不僅是重要的算法工具，更體現了"深度探索，回溯選擇"的思維方式。掌握 DFS 將為學習更復雜的算法奠定堅實基礎。   互動與分享

• 點贊👍 - 您的認可是我持續創作的最大動力

• 收藏⭐ - 方便隨時回顧這些重要的基礎概念

• 轉發↗️ - 分享給更多可能需要的朋友

• 評論💬 - 歡迎留下您的寶貴意見或想討論的話題

感謝您的耐心閲讀！ 關注博主，不錯過更多技術乾貨。我們下一篇再見！