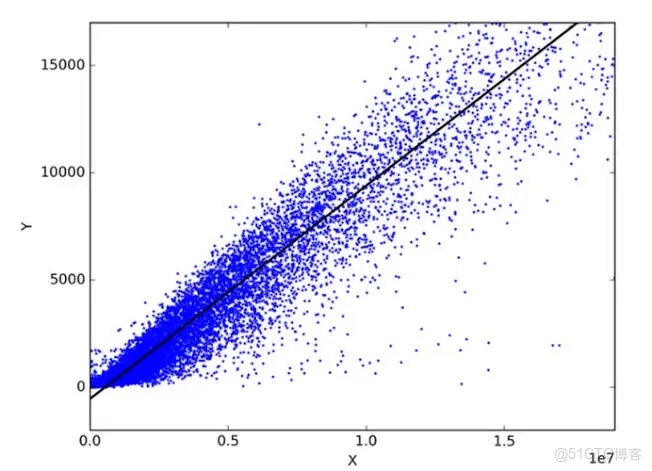
在現代科學研究與數據分析領域，理解變量之間的關係是一項核心任務。無論是在經濟預測、工程實驗還是生物統計分析中，研究者都面臨着大量複雜數據的挑戰。這些數據不僅維度多、噪聲強，而且變量之間的相互依賴往往難以直觀判斷。線性迴歸作為一種基礎而系統的量化工具，為這一問題提供了嚴謹的方法框架。通過數學模型，它將因變量與一個或多個自變量之間的關係形式化為線性函數，使研究者能夠定量評估自變量對因變量的影響，並在一定條件下進行科學推斷。

然而，線性迴歸的價值並不僅在於擬合數據曲線，更在於其深厚的理論基礎。它建立在統計學假設與優化理論之上，通過最小化誤差平方和實現參數估計，並通過矩陣代數與概率理論支撐推斷的有效性。在面對複雜、噪聲豐富的數據時，線性迴歸的數學結構與統計性質為科學分析提供了明確標準。理解線性迴歸，不僅是掌握一種建模方法，更是理解數據、變量關係以及科學推理過程的重要步驟。

隨着計算能力提升和數據量激增，線性迴歸的應用場景不斷拓展，從經典的橫截面分析到高維數據建模，再到時間序列和麪板數據分析，其理論與實踐價值仍然顯著。因此，深入研究線性迴歸的內涵、假設條件、估計方法與模型評價，既是掌握統計工具的前提，也是開展科學研究、實現精確量化分析的重要基礎。

1. 線性迴歸的基本定義與數學形式

線性迴歸是統計學中用於描述因變量與一個或多個自變量之間線性關係的核心方法。在最基本的形式中，線性迴歸假定因變量可以通過自變量的線性組合與誤差項表示，即：

其中，是截距項，為迴歸係數，表示誤差項。迴歸係數反映每個自變量對因變量的平均影響強度，而誤差項則捕捉模型未能解釋的部分。

在單變量情形下，模型簡化為：

迴歸係數可以通過最小二乘法求解，表示自變量每變化一單位時，因變量的平均變化量，截距表示當時的理論期望值。

1.1 最小二乘法

線性迴歸參數估計的核心方法是最小二乘法（Ordinary Least Squares, OLS）。其基本思想是選擇迴歸係數，使實際觀測值與模型預測值的殘差平方和最小化。數學表達式為：

對所有求偏導並令其為零，可得到解析解。對於單變量回歸，解析解為：

其中，與分別為樣本均值。

1.2 多變量回歸的矩陣形式

當自變量數量增加時，線性迴歸可以用矩陣形式表示。設設計矩陣為：

最小二乘估計的解析解為：

矩陣形式提供了高維擴展的基礎，也便於引入數值優化方法和正則化技術。

2. 線性迴歸的假設條件與理論基礎

線性迴歸的理論有效性建立在一系列明確的統計假設上，這些假設決定了參數估計、推斷及預測的可靠性。主要包括：

2.1 線性假設

迴歸模型假設因變量與自變量之間的關係是線性的，即：

這一假設保證了最小二乘估計可以正確描述變量間的平均線性關係。若實際關係高度非線性，則模型可能出現系統性偏差。

2.2 零均值假設

誤差項應滿足條件期望為零：

這一條件確保迴歸係數是無偏估計，即。若誤差項與自變量相關，則迴歸係數可能出現偏差，影響模型解釋力。

2.3 同方差性

誤差項的方差應保持恆定：

同方差性保證迴歸係數的標準誤差計算有效。如果誤差呈異方差性，參數估計仍可無偏，但推斷結果可能不可靠，需要使用穩健標準誤差。

2.4 獨立性

誤差項之間應相互獨立：

獨立性假設是迴歸分析推斷的基礎，尤其在時間序列或空間數據中，自相關可能導致係數標準誤差低估。

2.5 正態性（可選）

在推斷階段，通常假設誤差項服從正態分佈：

正態性假設主要用於構建迴歸係數的置信區間、進行t檢驗和F檢驗。如果樣本量足夠大，中心極限定理允許在一定程度上放寬正態性要求。

2.6 Gauss-Markov定理

在假設1至4成立的前提下，最小二乘估計具有**最佳線性無偏估計（BLUE）**性質，即在所有線性無偏估計中，最小二乘估計的方差最小：

這一性質是線性迴歸理論的核心支撐，也是迴歸分析在統計推斷中可靠性的基礎。

3. 迴歸係數估計與解釋

3.1 單變量回歸係數估計

單變量線性迴歸中，迴歸係數可以通過解析公式直接計算：

其中與分別為自變量與因變量的樣本均值。這一公式揭示了迴歸係數與樣本協方差、方差的關係，説明迴歸係數不僅是擬合參數，更反映了數據分佈特徵。

3.2 多變量回歸係數估計

對於多變量回歸，迴歸係數的解析解可表示為矩陣形式：

其中為的設計矩陣，第一列通常為常數1（對應截距項），為的因變量向量。矩陣形式便於擴展到高維數據分析，也為數值優化和正則化方法提供基礎。

3.3 係數解釋

迴歸係數的解釋需要考慮控制變量。在多變量模型中，表示在其他自變量保持不變的條件下，變化一單位對的平均影響。這一條件性解釋對於經濟學、社會科學和生物統計的因果分析至關重要。

4. 模型評價指標與假設檢驗

線性迴歸的一個核心問題是如何評價模型擬合效果及參數顯著性。主要方法包括：

1. 決定係數：衡量自變量對因變量變異解釋能力的比例。，其中為總平方和。越接近1，説明模型擬合越好。
2. 調整：針對多變量模型，調整自由度後更合理地評價模型擬合能力。
3. F檢驗：檢驗整個迴歸模型是否顯著，考察自變量整體對因變量的解釋能力。
4. t檢驗：檢驗單個迴歸係數是否顯著不為零，即自變量是否對因變量具有顯著線性影響。
5. 殘差分析：通過繪製殘差圖、檢驗異方差性和自相關性，評估模型假設是否滿足。

這些評價指標與檢驗方法不僅是擬合結果的量化工具，也為模型改進、變量選擇及進一步的理論推導提供依據。

5. 線性迴歸的擴展與高級應用

5.1 正則化方法

在高維數據或自變量高度相關的情況下，普通最小二乘迴歸可能出現過擬合或不穩定。正則化方法通過引入約束項改善模型性能，包括：

• 嶺迴歸（Ridge Regression）：在目標函數中加入，控制係數大小，緩解多重共線性問題。
• 套索迴歸（Lasso Regression）：在目標函數中加入，同時實現變量選擇與參數收縮。

這些方法不僅提高預測精度，也使模型更具可解釋性。

5.2 廣義線性模型

線性迴歸假設因變量連續且誤差正態分佈，但現實中可能有二分類、計數等非連續數據。廣義線性模型（GLM）通過連接函數（link function）擴展線性迴歸，使其適用於更廣泛的數據類型。例如，邏輯迴歸用於二分類問題，泊松迴歸用於計數數據分析。

5.3 時間序列迴歸與面板數據迴歸

在經濟學、金融學和工程領域，數據具有時間序列或跨單位結構。線性迴歸可以結合滯後變量、固定效應和隨機效應模型，處理時間依賴性和單位間差異。例如：

其中表示個體，表示時間，控制個體固定效應。這種擴展將線性迴歸從橫截面分析拓展至動態和多維結構分析。

6. 數據質量與模型適用性

線性迴歸的有效性高度依賴數據質量。異常值、測量誤差和自變量多重共線性都會影響參數估計和預測能力。例如，多重共線性可能導致迴歸係數波動巨大，顯著性檢驗失效；異常值可能對最小二乘法估計產生強烈影響。在實踐中，常用的解決方案包括數據預處理、穩健迴歸、變量轉換以及正則化方法。

此外，模型適用性也需要謹慎評估。線性迴歸適用於變量關係近似線性的場景，而對於高度非線性或交互複雜的系統，其預測能力有限。在這種情況下，可以考慮多項式迴歸、核方法或非線性迴歸模型作為替代。

7. 數學性質與統計理論支撐

線性迴歸模型不僅提供了數據擬合工具，其數學性質和統計理論基礎也是研究者關注的重要部分。最小二乘估計具有線性性，即迴歸係數是因變量的線性組合。同時，在滿足Gauss-Markov條件下，最小二乘估計是藍色估計（Best Linear Unbiased Estimator, BLUE），即在所有線性無偏估計中方差最小。

迴歸分析還涉及矩陣代數、最優化理論和概率統計知識。例如，矩陣的條件數影響迴歸係數的穩定性；協方差矩陣提供係數標準誤差計算基礎；誤差正態性假設允許構建置信區間和假設檢驗。

8. 線性迴歸的應用意義

從科學研究角度看，線性迴歸不僅是數據擬合手段，更是一種認知工具。通過構建線性關係模型，研究者可以：

• 定量評估變量之間的依賴強度；
• 探索潛在機制及變量間的因果提示；
• 為進一步複雜建模提供參數初值和結構假設。

在實踐中，線性迴歸被廣泛用於經濟預測、市場分析、環境科學等領域。其核心優勢在於數學結構清晰、結果易於解釋，並能通過統計推斷提供定量依據。

然而，線性迴歸也面臨侷限。它無法直接處理高度非線性關係、變量交互複雜的情況，也依賴於數據滿足一定假設條件。理解這些侷限性，才能在實際應用中做出科學判斷，並結合正則化、非線性擴展、廣義線性模型等方法提升模型能力。

9. 總結

線性迴歸是一種科學、數學嚴密的數據建模方法，它不僅用於預測和擬合，更提供了理解變量關係、驗證假設和指導決策的理論工具。通過最小二乘法、矩陣運算、正則化方法及廣義線性擴展，線性迴歸在理論深度和應用廣度上均表現出強大的價值。研究線性迴歸的核心不僅在於掌握公式和軟件操作，而在於理解其數學結構、統計假設及數據依賴關係，從而在科學研究和工程實踐中實現量化分析與合理推斷。

隨着數據科學的發展，線性迴歸依然保持其理論位置和實踐價值。無論是在高維數據分析、時間序列建模，還是在複雜社會經濟系統的定量研究中，線性迴歸及其擴展模型都為研究者提供了可靠的分析框架和方法論指導。深入理解線性迴歸，不僅提升數據分析能力，也有助於培養科學建模思維，為探索複雜系統提供基礎工具。