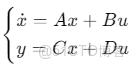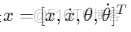% 物理參數
M = 1.096;    % 小車質量 (kg)
m = 0.109;    % 擺杆質量 (kg)
l = 0.25;     % 擺長 (m)
g = 9.8;      % 重力加速度 (m/s²)
b = 0.1;      % 摩擦係數
I = 0.0034;   % 擺杆轉動慣量 (kg·m²)

% 狀態空間矩陣
A = [0 1 0 0;
     0 -(I+m*l²)*b/(I*(M+m)+M*m*l²) m²*g*l²/(I*(M+m)+M*m*l²) 0;
     0 0 0 1;
     0 -m*b*l/(I*(M+m)+M*m*l²) m*g*l*(M+m)/(I*(M+m)+M*m*l²) 0];
B = [0; (I+m*l²)/(I*(M+m)+M*m*l²); 0; -m*l/(I*(M+m)+M*m*l²)];
C = eye(4);
D = zeros(4,1);

Q = diag([1000, 0, 200, 0]);  % 狀態權重
R = 1;                        % 控制輸入權重

[K, P, E] = lqr(A, B, Q, R);

% 初始狀態 [x, x_dot, theta, theta_dot]
x0 = [0.1; 0; 0.1; 0]; 

% 閉環系統矩陣
A_cl = A - B*K;
sys_cl = ss(A_cl, B, C, D);

% 仿真參數
t = 0:0.01:5;
u = 0.1*ones(size(t));  % 階躍輸入

% 仿真
[y, t] = lsim(sys_cl, u, t, x0);

% 繪圖
figure;
subplot(2,1,1);
plot(t, y(:,1), 'r', t, y(:,3), 'b');
xlabel('時間 (s)');
ylabel('位置 (m)/角度 (rad)');
legend('小車位置', '擺杆角度');
title('LQR控制響應');

subplot(2,1,2);
stem(t, u*1000);
xlabel('時間 (s)');
ylabel('控制輸入 (mN)');
title('LQR控制量');

Kp = 50;    % 比例係數
Ki = 10;    % 積分系數
Kd = 10;    % 微分系數

% PID控制器
pid = pid(Kp, Ki, Kd);

% 閉環系統矩陣
A_pid = A - B*pid.C;
sys_pid = ss(A_pid, B, C, D);

% 仿真
[y_pid, t_pid] = lsim(sys_pid, u, t, x0);

% 繪圖對比
figure;
subplot(2,1,1);
plot(t, y(:,1), 'r', t_pid, y_pid(:,1), 'b--');
hold on;
plot(t, y(:,3), 'g', t_pid, y_pid(:,3), 'm--');
legend('LQR位置', 'PID位置', 'LQR角度', 'PID角度');
title('PID與LQR控制對比');

subplot(2,1,2);
plot(t, u*1000, 'r', t_pid, pid.out*1000, 'b--');
xlabel('時間 (s)');
ylabel('控制輸入 (mN)');
legend('LQR控制量', 'PID控制量');

%% 一級倒立擺控制仿真
clear; clc;

%% 系統參數
M = 1.096; m = 0.109; l = 0.25; g = 9.8; b = 0.1; I = 0.0034;

% 狀態空間模型
A = [0 1 0 0;
     0 -(I+m*l²)*b/(I*(M+m)+M*m*l²) m²*g*l²/(I*(M+m)+M*m*l²) 0;
     0 0 0 1;
     0 -m*b*l/(I*(M+m)+M*m*l²) m*g*l*(M+m)/(I*(M+m)+M*m*l²) 0];
B = [0; (I+m*l²)/(I*(M+m)+M*m*l²); 0; -m*l/(I*(M+m)+M*m*l²)];
C = eye(4); D = zeros(4,1);

%% LQR控制
Q = diag([1000, 0, 200, 0]); R = 1;
[K, P, E] = lqr(A, B, Q, R);
A_cl = A - B*K;
sys_cl = ss(A_cl, B, C, D);

%% PID控制
Kp = 50; Ki = 10; Kd = 10;
pid = pid(Kp, Ki, Kd);
A_pid = A - B*pid.C;
sys_pid = ss(A_pid, B, C, D);

%% 仿真
t = 0:0.01:5;
u = 0.1*ones(size(t));
x0 = [0.1; 0; 0.1; 0];

% LQR仿真
[y_lqr, t_lqr] = lsim(sys_cl, u, t, x0);

% PID仿真
[y_pid, t_pid] = lsim(sys_pid, u, t, x0);

%% 結果可視化
figure;
subplot(2,1,1);
plot(t_lqr, y_lqr(:,1), 'r', t_pid, y_pid(:,1), 'b--');
hold on;
plot(t_lqr, y_lqr(:,3), 'g', t_pid, y_pid(:,3), 'm--');
xlabel('時間 (s)');
ylabel('位置 (m)/角度 (rad)');
legend('LQR位置', 'PID位置', 'LQR角度', 'PID角度');

subplot(2,1,2);
stem(t_lqr, u*1000, 'r', t_pid, pid.out*1000, 'b--');
xlabel('時間 (s)');
ylabel('控制輸入 (mN)');
legend('LQR控制量', 'PID控制量');