主要目的
- 提高模型性能:移除不相關或冗餘的特徵可以減少“維度災難”效應,避免模型過度擬合訓練數據,從而在測試集上獲得更好的泛化能力。
- 降低模型複雜度:特徵越少,模型結構越簡單,訓練和預測速度越快。
- 增強模型可解釋性:使用更少、更核心的特徵,使得模型的決策過程更容易被理解和解釋。
常用的特徵選擇方法
常用的特徵選擇方法包括過濾法、包裹法和嵌入法
過濾法
過濾法獨立於任何特定的機器學習模型,僅根據特徵本身的內在屬性(如與目標變量的相關性、信息量等)進行評分和排序,然後選取得分最高的特徵。
優點
- 計算效率高,速度快。
- 不依賴於特定的學習算法。
缺點:忽略了特徵間的交互作用和模型本身的特性。
常用的方法有
- 方差閾值
如果一個特徵的方差很小,説明其取值變化不大,對模型訓練的貢獻很小,可以被移除。 - 卡方檢驗 ( Test):
用於分類任務,檢驗特徵與類別變量的獨立性。
卡方值越大,意味着特徵與標籤之間存在顯著關聯。 - 相關係數
衡量特徵 與目標變量 之間的線性關係。通常使用皮爾遜相關係數。
絕對值越大,説明線性相關性越強。 - 信息增益
衡量分類問題中,使用特徵 後,目標變量 的不確定性(熵)減少了多少。 - 互信息
衡量變量間的非線性依賴關係,
值越大表示特徵與目標變量之間的信息共享越多。
互信息越大,説明特徵對目標的信息貢獻越大。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_california_housing
from sklearn.feature_selection import mutual_info_regression
import seaborn as sns
# 加載加州房價數據集
data = fetch_california_housing(as_frame=True)
X = data.data
y = data.target
# 計算皮爾遜相關係數
corr = X.corrwith(y)
# 計算互信息
mi = mutual_info_regression(X, y, random_state=42)
# 可視化特徵重要性
fig, ax = plt.subplots(1, 2, figsize=(14, 5))
# 皮爾遜相關係數圖
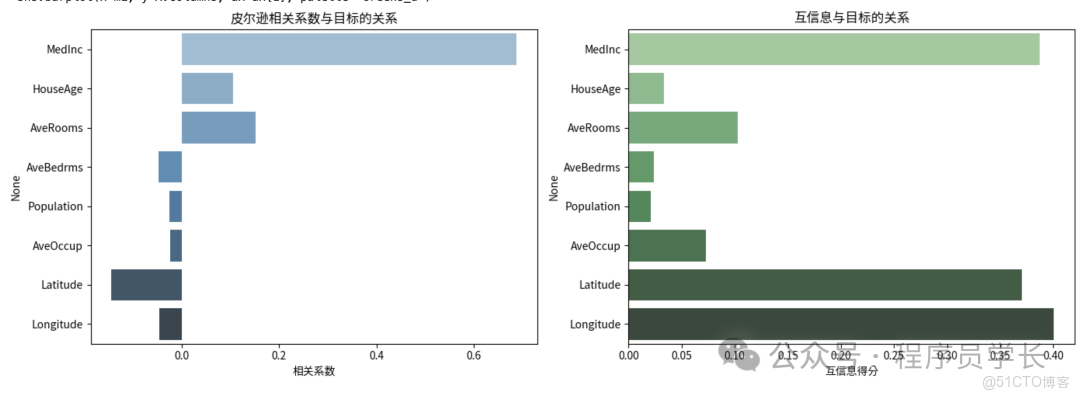
sns.barplot(x=corr.values, y=corr.index, ax=ax[0], palette="Blues_d")
ax[0].set_title("皮爾遜相關係數與目標的關係")
ax[0].set_xlabel("相關係數")
# 互信息圖
sns.barplot(x=mi, y=X.columns, ax=ax[1], palette="Greens_d")
ax[1].set_title("互信息與目標的關係")
ax[1].set_xlabel("互信息得分")
plt.tight_layout()
plt.show()包裹法
包裹法通過實際訓練模型來評估特徵子集的優劣。核心思想是:以模型性能(如準確率、MSE、AUC)作為評價標準,通過搜索算法選擇最優特徵組合。
包裹法將特徵選擇過程看作是一個搜索問題,它使用特定的學習算法作為 “黑盒評估器”,以模型性能(如準確率、MSE、AUC)作為評價標準,通過迭代地選擇特徵子集,最終找到使該評估器性能最優的特徵子集。
優點:
- 能找到最適合特定學習器的特徵子集。
- 能考慮特徵之間的相互作用。
缺點:計算成本非常高,因為它需要對每個子集進行模型訓練和評估。
常用的方法有
- 向前選擇:從空集開始,每次添加一個使性能提升最大的特徵,直到性能不再顯著提升。
- 向後消除:從所有特徵開始,每次移除一個使性能下降最小的特徵,直到性能下降到不可接受的程度。
- 遞歸特徵消除 (RFE)
- 使用所有特徵訓練一個模型。
- 根據模型係數(如線性模型)或特徵重要性(如樹模型)移除最不重要的特徵。
- 重複步驟 1 和 2,直到達到預設的特徵數量或性能閾值。
from sklearn.linear_model import LinearRegression
from sklearn.feature_selection import RFE
# 使用線性迴歸模型進行遞歸特徵消除
model = LinearRegression()
rfe = RFE(model, n_features_to_select=5)
rfe.fit(X, y)
# 提取被選中的特徵
selected_features = X.columns[rfe.support_]
ranking = rfe.ranking_
# 可視化結果
plt.figure(figsize=(8, 5))
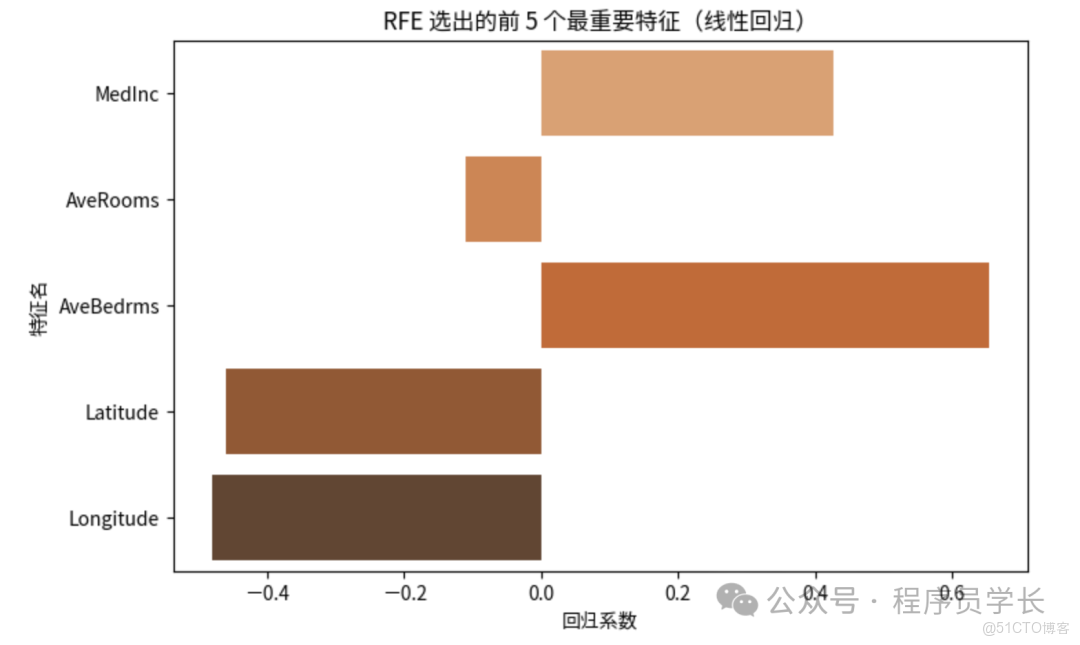
sns.barplot(x=rfe.estimator_.coef_, y=selected_features, palette="Oranges_d")
plt.title("RFE 選出的前 5 個最重要特徵(線性迴歸)")
plt.xlabel("迴歸係數")
plt.ylabel("特徵名")
plt.show()
print("被選擇的特徵:", list(selected_features))嵌入法
嵌入法在模型訓練過程中自動完成特徵選擇,兼顧了性能與效率。
優點:兼顧了過濾法的高效率和包裹法的模型契合度,計算效率比包裹法高得多。
缺點:選擇的特徵子集依賴於所選的特定模型。
常用的方法有
- L1正則化(Lasso迴歸)
Lasso 迴歸通過在損失函數中加入 正則項,使部分特徵權重收縮為 0,從而實現特徵選擇。 - 基於樹模型的重要性排序
決策樹、隨機森林、XGBoost 等算法可根據特徵在分裂節點中帶來的信息增益或基尼指數下降來計算特徵重要性。
重要性高的特徵被保留。
from sklearn.linear_model import LassoCV
from sklearn.preprocessing import StandardScaler
# 特徵標準化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# 使用帶交叉驗證的 Lasso
lasso = LassoCV(cv=5, random_state=42)
lasso.fit(X_scaled, y)
# 獲取特徵權重
coef = pd.Series(lasso.coef_, index=X.columns)
# 可視化
plt.figure(figsize=(10, 6))
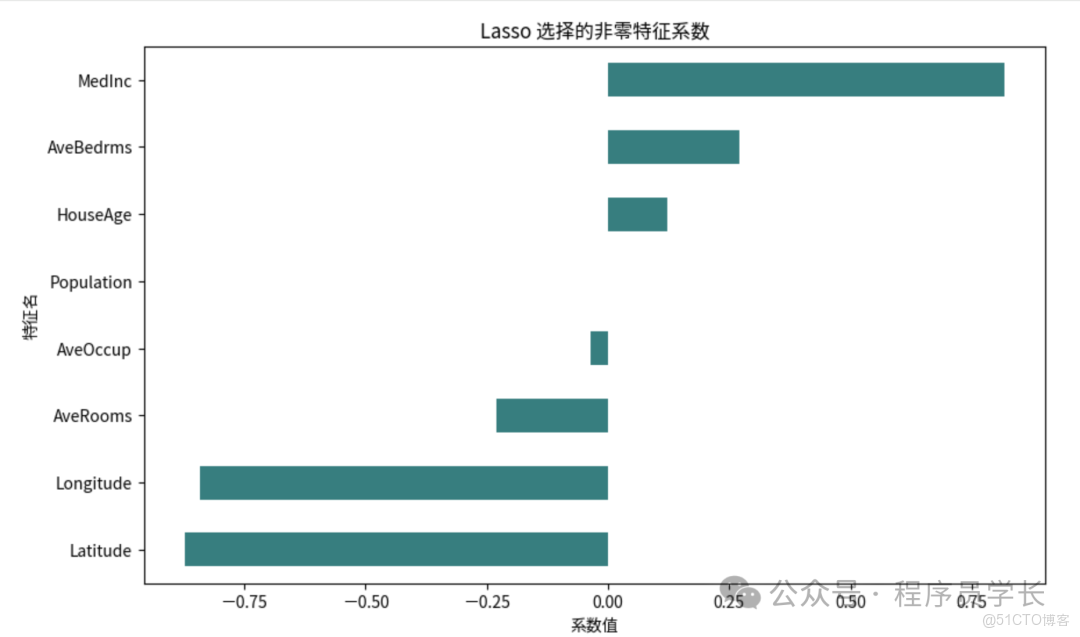
coef[coef != 0].sort_values().plot(kind="barh", color="teal")
plt.title("Lasso 選擇的非零特徵係數")
plt.xlabel("係數值")
plt.ylabel("特徵名")
plt.show()
print("Lasso 選擇的關鍵特徵:", list(coef[coef != 0].index))