在數據可視化世界中,我們經常用直方圖來描述數據的分佈情況,但今天我想介紹兩種特別而優雅的點狀圖變體:威爾金森點狀圖和麥穗圖。
它們像數據世界的"點彩派"畫家,用簡單的點創造出豐富的信息層次。
與直方圖相比,這種點繪法不僅能夠更直觀地展示數據分佈的細節,還能更好地揭示數據之間的關係和模式,使得觀察者能夠從更廣闊的視角理解數據集的特點。
1. 威爾金森點狀圖
想象一下,你有一袋彩色彈珠,需要按顏色分類展示。如果只是簡單地把所有彈珠倒出來,它們會雜亂無章。
但如果你為每種顏色準備一個小盒子,把相同顏色的彈珠整齊地堆疊在裏面,這就是威爾金森點狀圖的基本思想。
威爾金森點狀圖將數據點堆疊在對應的數值區域,形成類似直方圖的分佈展示,但保留了每個數據點的個體性。
它不是用條形的高度表示頻率,而是用實際的數據點數量來可視化分佈。
下面基於matplotlib庫封裝了一個繪製威爾金森點狀圖的函數。
def wilkinson_dot_plot(
data, bins=10, dot_size=40, dot_spacing=0.8, show_stats=True, random_seed=42
):
"""
創建威爾金森點狀圖
參數:
data: 輸入數據(一維數組)
bins: 分組數量或分組邊界
dot_size: 點的大小
dot_spacing: 點之間的垂直間距
random_seed: 隨機種子
"""
np.random.seed(random_seed)
# 創建圖形
fig, ax = plt.subplots(figsize=(10, 7))
# 計算直方圖數據
hist, bin_edges = np.histogram(data, bins=bins)
# 為每個分組創建點
max_count = 0 # 記錄最大堆疊高度
bin_centers = [] # 保存每個分組的中心位置
# 省略...
plt.tight_layout()
return fig, ax, (bin_edges, hist)
威爾金森點狀圖的核心算法可以分解為幾個步驟:
- 數據分箱:將連續數據分成若干個等寬的區間
- 點位置計算:在每個區間內,將數據點垂直堆疊
- 避免重疊:通過調整點的垂直位置防止重疊,同時保持可讀性
使用起來也簡單:
# 生成示例數據
np.random.seed(42)
# 數據集:正態分佈
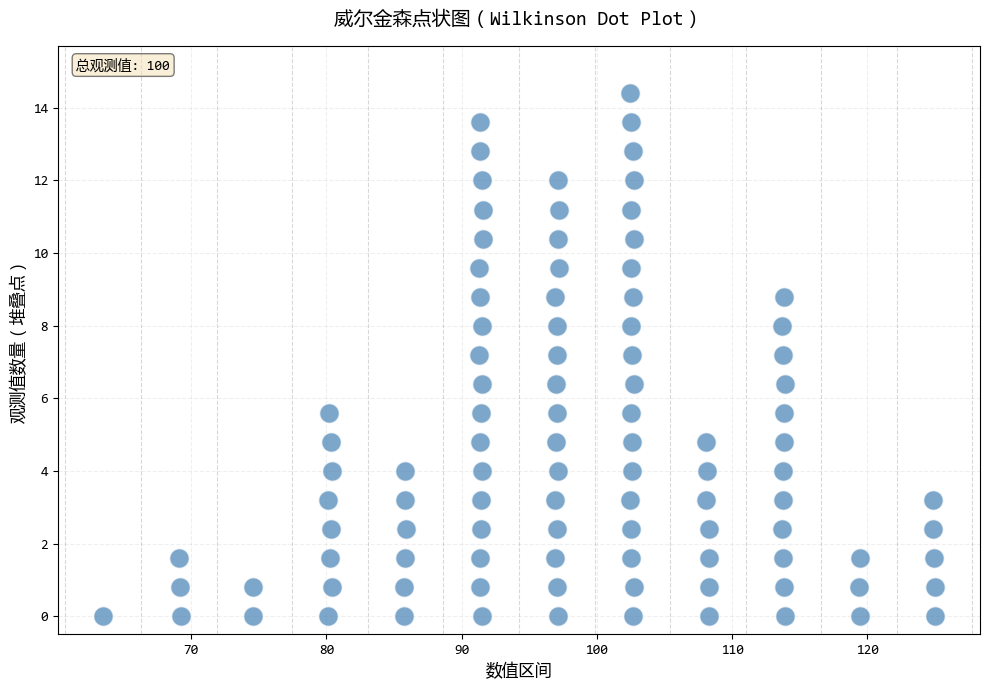
data_normal = np.random.normal(100, 15, 100)
dot_size = 200
# 創建威爾金森點狀圖
fig1, ax1, stats1 = wilkinson_dot_plot(data_normal, bins=12, dot_size=dot_size)
plt.show()
2. 麥穗圖
如果把威爾金森點狀圖比作整齊堆疊的彈珠,那麼麥穗圖就像是田野中的麥穗——每個數據點都像一顆麥粒,精確地生長在自己的位置上,展示其實際數值。
麥穗圖是威爾金森點狀圖的一種變體,它將點放置在其實際數值位置,而不是分組中心。
這保留了數據的精確性,同時通過堆疊避免了重疊。
麥穗圖的實現與威爾金森點狀圖類似,但有一個關鍵區別:點沿x軸放置在實際數據值位置,而不是分組中心。
# 封裝麥穗圖函數
def strip_plot(
data,
bin_edges=None,
bins=10,
dot_size=40,
dot_spacing=0.8,
jitter_amount=0.2,
random_seed=42,
):
"""
創建麥穗圖(在威爾金森點狀圖基礎上顯示實際值)
參數:
data: 輸入數據(一維數組)
bin_edges: 可選,使用預定義的分組邊界
bins: 如果未提供bin_edges,則使用此參數創建分組
dot_size: 點的大小
dot_spacing: 點之間的垂直間距
jitter_amount: 水平抖動程度(避免重疊)
random_seed: 隨機種子
"""
np.random.seed(random_seed)
# 創建圖形
fig, ax = plt.subplots(figsize=(10, 7))
# 如果沒有提供分組邊界,則計算
if bin_edges is None:
hist, bin_edges = np.histogram(data, bins=bins)
else:
hist, bin_edges = np.histogram(data, bins=bin_edges)
# 對數據進行排序
sorted_data = np.sort(data)
# 將數據分配到對應的分組
data_by_bin = []
for i in range(len(bin_edges) - 1):
lower, upper = bin_edges[i], bin_edges[i + 1]
bin_data = sorted_data[(sorted_data >= lower) & (sorted_data < upper)]
data_by_bin.append(bin_data)
# 處理最後一個分組(包含最大值)
if len(data) > 0:
last_bin_data = sorted_data[sorted_data >= bin_edges[-2]]
if len(data_by_bin) > 0:
data_by_bin[-1] = last_bin_data
# 繪製麥穗圖
max_points_in_bin = 0
# 省略 ...
plt.tight_layout()
return fig, ax, (bin_edges, data_by_bin)
使用起來也簡單:
# 生成示例數據
np.random.seed(42)
# 數據集:正態分佈
data_normal = np.random.normal(100, 15, 100)
dot_size = 200
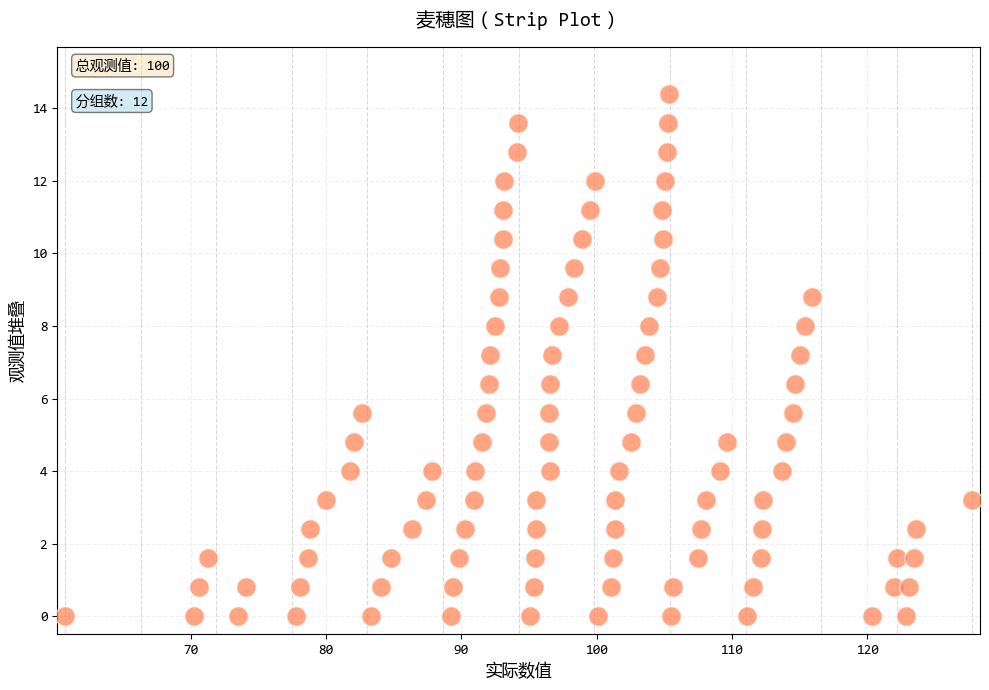
# 創建的麥穗圖
bin_edges = 12
fig2, ax2, stats2 = strip_plot(
data_normal, bin_edges=bin_edges, dot_size=dot_size, jitter_amount=0.15
)
plt.show()
3. 兩種圖的應用場景
下面模擬一個學生考試成績分佈的分析場景,看看上面兩種點狀圖的應用。
# 示例:學生考試成績分佈分析
print("示例:學生考試成績分佈分析")
print("-" * 40)
# 創建模擬的考試成績數據
np.random.seed(42)
exam_scores = np.concatenate(
[
np.random.normal(65, 8, 45), # 中等水平學生
np.random.normal(85, 6, 30), # 優秀學生
np.random.normal(45, 10, 24), # 需要幫助的學生
]
)
# 過濾掉不合理分數
exam_scores = np.clip(exam_scores, 0, 100)
print(f"學生總數: {len(exam_scores)}")
print(f"分數範圍: {exam_scores.min():.1f} - {exam_scores.max():.1f}")
print(f"平均分: {exam_scores.mean():.1f}")
print(f"及格率: {(exam_scores >= 60).sum() / len(exam_scores) * 100:.1f}%\n")
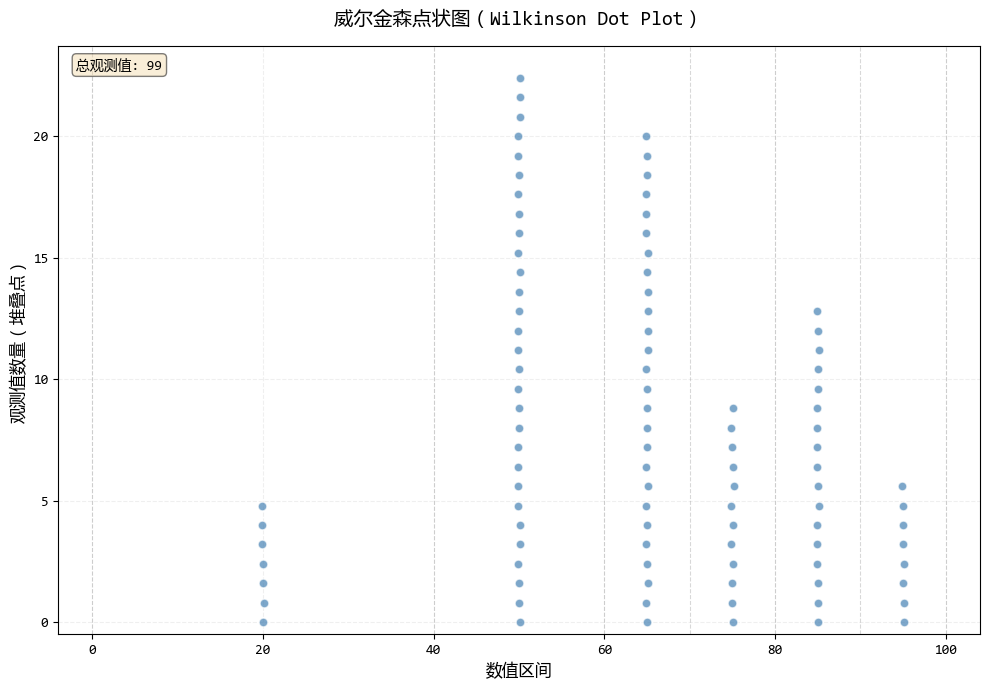
# 使用威爾金森點狀圖
print("創建威爾金森點狀圖...")
fig1, ax1, stats1 = wilkinson_dot_plot(
exam_scores,
bins=[0, 40, 60, 70, 80, 90, 100],
)
plt.show()
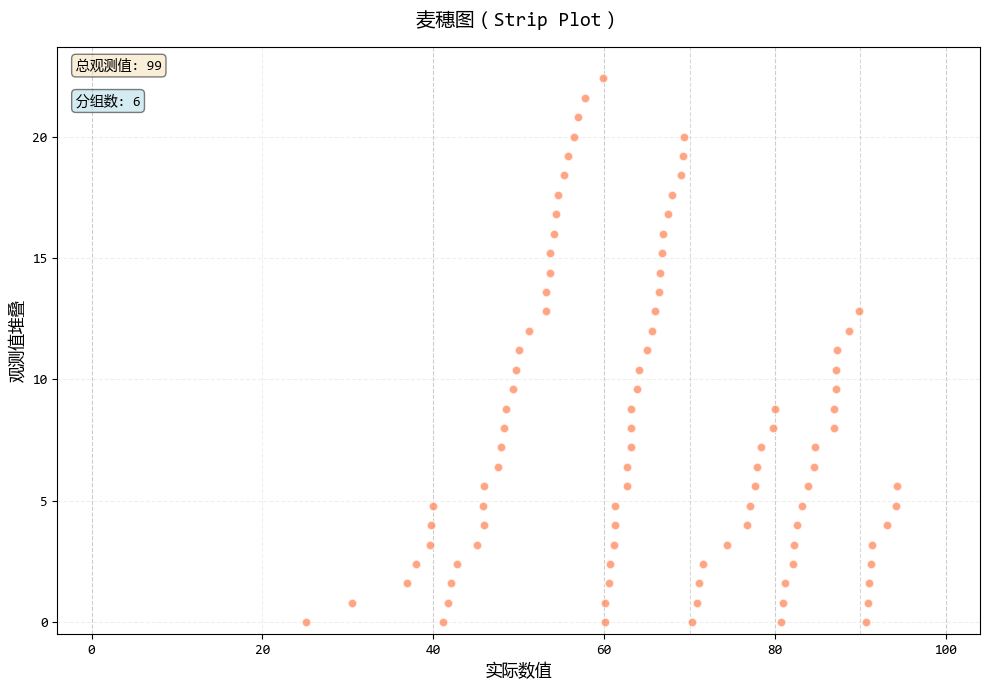
# 使用麥穗圖
print("創建麥穗圖...")
fig2, ax2, stats2 = strip_plot(
exam_scores,
bins=[0, 40, 60, 70, 80, 90, 100],
jitter_amount=0.15,
)
plt.show()
## 輸出結果:
'''
示例:學生考試成績分佈分析
----------------------------------------
學生總數: 99
分數範圍: 25.1 - 94.4
平均分: 65.3
及格率: 63.6%
'''
在學生考試成績分析這個場景中:
- 威爾金森點狀圖:將分數分組成區間(如60-70分),所有該區間的學生點都堆疊在區間中心,清晰地展示了分數段的整體分佈形態,類似直方圖但能看到個體點。
- 麥穗圖:點在實際分數位置堆疊(如65分、68分等),既顯示了每個學生的具體分數,又通過垂直堆疊避免了重疊,保留了數據的精確性。
總的來説,威爾金森點狀圖看分佈形態(區間視角),麥穗圖看具體數值(精確視角)。
4. 總結
威爾金森點狀圖和麥穗圖為數據可視化工具箱增添了優雅而實用的工具。
它們填補了傳統直方圖和散點圖之間的空白,提供了同時展示數據分佈和個體數據點的獨特方式。
在數據可視化中,選擇合適的圖表類型就像選擇正確的工具來完成工作。
威爾金森點狀圖和麥穗圖提供了獨特的視角,讓我們能夠同時看到森林和樹木——既理解整體分佈,又關注個體數據點。
完整代碼分享:威爾金森與麥穗圖.ipynb (訪問密碼: 6872)