數據結構與算法 Detail - 數據結構和算法,鏈表,雙向鏈表,棧,隊列測試菜鳥 Blog

Stories

Detail

Return

數據結構與算法 - Stories Detail

06:17 PM · Nov 06 ,2025

一、算法

1.1、算法基礎

概念：算法是獨⽴存在的⼀種解決問題的⽅法和思想
算法的特性：

輸入：算法具有0個或多個輸⼊
輸出: 算法⾄少有1個或多個輸出
有窮性: 算法在有限的步驟之後會⾃動結束⽽不會⽆限循環，並且每⼀個步驟可以在可接受的時間內完成
確定性：算法中的每⼀步都有確定的含義，不會出現⼆義性
可⾏性：算法的每⼀步都是可⾏的，也就是説每⼀步都能夠執⾏有限的次數完成

1.2、算法效率衡量

⼤O記法	對於單調的整數函數f，如果存在⼀個整數函數g和實常數c>0，使得對於充分⼤的n總有f(n)<=c*g(n)，就説函數g是f的⼀個漸近函數（忽略常數），記為f(n)=O(g(n))。也就是説，在趨向⽆窮的極限意義下，函數f的增⻓速度受到函數g的約束，亦即函數f與函數g的特徵相似
時間複雜度	假設存在函數g，使得算法A處理規模為n的問題示例所⽤時間為T(n)=O(g(n))，則稱O(g(n))為算法A的漸近時間複雜度，簡稱時間複雜度，記為T(n)

理解“⼤O記法”

對於算法的時間性質和空間性質，最重要的是其數量級和趨勢，這些是分析
算法效率的主要部分。⽽計量算法基本操作數量的規模函數中那些常量因⼦
可以忽略不計。例如，可以認為3n^2 和100n^2 屬於同⼀個量級，如果兩個算法
處理同樣規模實例的代價分別為這兩個函數，就認為它們的效率“差不多”，
都為n^2 級

複雜度分類	解釋説明	分析哪個複雜度為最優
最優時間複雜度	算法完成⼯作最少需要多少基本操作	價值不⼤，因為它沒有提供什麼有⽤信息，其反映的只是最樂觀最理想的情況，沒有參考價值
最壞時間複雜度	算法完成⼯作最多需要多少基本操作	提供了⼀種保證，表明算法在此種程度的基本操作中⼀定能完成⼯作
平均時間複雜度	算法完成⼯作平均需要多少基本操作	對算法的⼀個全⾯評價，因此它完整全⾯的反映了這個算法的性質。但另⼀⽅⾯，這種衡量並沒有保證，不是每個計算都能在這個基本操作內完成。⽽且，對於平均情況的計算，也會因為應⽤算法的實例分佈可能並不均勻⽽難以計算

因此，只需關注算法的最壞情況，亦即最壞時間複雜度

時間複雜度的計算規則：
1.基本操作，即只有常數項，認為其時間複雜度為O(1)
2.順序結構，時間複雜度按加法進⾏計算
3.循環結構，時間複雜度按乘法進⾏計算
4.分⽀結構，時間複雜度取最⼤值
5.判斷⼀個算法的效率時，往往只需要關注操作數量的最⾼次項，其它次要項和常數項可以忽略
6.在沒有特殊説明時，我們所分析的算法的時間複雜度都是指最壞時間複雜度

空間複雜度S(n)

空間複雜度(SpaceComplexity)是對⼀個算法在運⾏過程中臨時佔⽤存儲空間⼤⼩的量度
算法的時間複雜度和空間複雜度合稱為算法的複雜度

1.3、常見的時間複雜度

執行次數函數	階	非正式術語
100	O(1)	常數階
2n+1	O(n)	線性階
3n²+2n+1	O(n²)	平方階
4n³+3n²+2n+1	O(n³)	立方階
2^n	O(2^n)	指數階
5log2n + 1	O(logn)	對數階
3nlog2n + 2n + 1	O(nlogn)	nlogn階

注意，將log2n（以2為底的對數）簡寫成logn

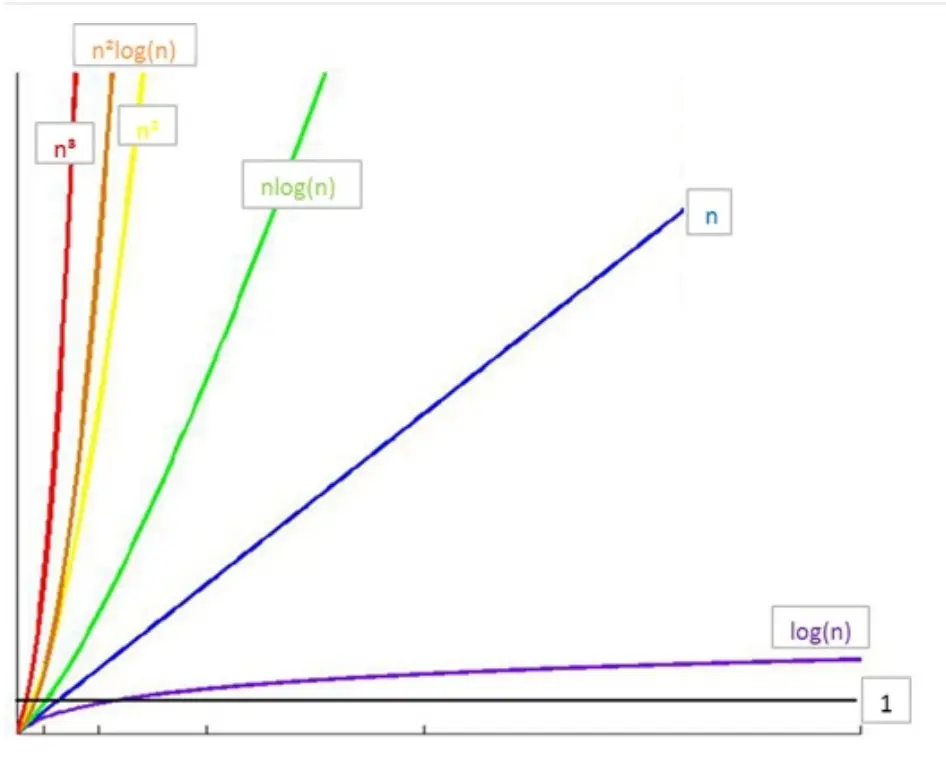
常⻅時間複雜度之間的關係

所消耗的時間從⼩到⼤
O(1) < O(logn) < O(n) < O(nlogn) < O(n²) < O(n³) < O(2^n) < O(n!) <O(n^n)

二、數據結構

2.1、數據結構基礎

數據是⼀個抽象的概念，將其進⾏分類後得到程序設計語⾔中的基本類型。如：int，float，char，bool等。
數據元素之間不是獨⽴的，存在特定的關係，這些關係便是結構(eg:一個人有名字和年齡，名字和年齡都屬於這個人，因此數據元素不是獨立的)
數據結構指數據對象中數據元素之間的關係

2.2、算法和數據結構的區別

算法	數據結構
⾼效的程序需要在數據結構的基礎上設計和選擇算法	數據結構只是靜態的描述了數據元素之間的關係
算法是為了解決實際問題⽽設計的	數據結構是算法需要處理的問題載體

綜上：程序 = 數據結構 + 算法

2.3、抽象數據類型(ADT)

抽象數據類型	面向對象中的封裝
指⼀個數學模型以及定義在此數學模型上的⼀組操作	class包含屬性和方法，屬性就是存儲的數據，方法就是對數據的操作
抽象數據類型就相當於面向對象中的封裝，因此相當於class的概念

常用的數據運算：插入、刪除、修改、查找、排序

2.4、基本的數據結構

2.4.1、順序表

2.4.1.1、順序表概念相關

將一組元素看成一個序列，用元素在序列裏的位置和順序，表示實際應用中的某種有意義的信息，或者表示數據之間的某種關係，這樣的一組序列元素的組織形式，抽象的稱為線性表，一個線性表是某類元素的一個集合，還記錄着元素之間的一種順序關係；

線性表兩種存儲形式：

順序表，將元素順序地存放在⼀塊連續的存儲區⾥，元素間的順序關係由它們的存儲順序⾃然表示
鏈表，將元素存放在通過鏈接構造起來的⼀系列存儲塊中

2.4.1.2、順序表的形式

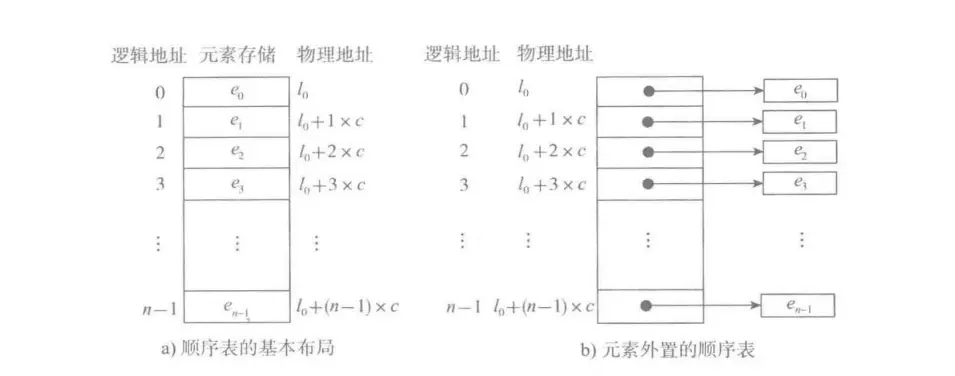
圖a	圖b
順序表的基本形式，數據元素本身連續存儲，每個元素所佔的存儲單元⼤⼩固定相同	如果元素的⼤⼩不統⼀，則須採⽤圖b的元素外置的形式，將實際數據元素另⾏存儲，⽽順序表中各單元位置保存對應元素的地址信息（即鏈接）
元素的下標是其邏輯地址，⽽元素存儲的物理地址（實際內存地址）可以通過存儲區的起始地址Loc (e )加上邏輯地址（第i個元素）與存儲單元⼤⼩（c）的乘積計算⽽得，即：Loc(e ) = Loc(e ) + c*	圖b中的c不再是數據元素的⼤⼩，⽽是存儲⼀個鏈接地址所需的存儲量，這個量通常很⼩

**訪問指定元素時⽆需從頭遍歷，通過計算便可獲得對應地址，其時間復
雜度為O(1)**

2.4.1.3、順序表的結構與實現

結構：

順序表的完整信息包含兩個部分：

1、表中的元素集合
2、實現正確操作而需記錄的信息(有關表的整體情況的信息，
這部分信息主要包括存儲區的**容量**和當前表中已有的**元素個數**)

兩種實現方式：

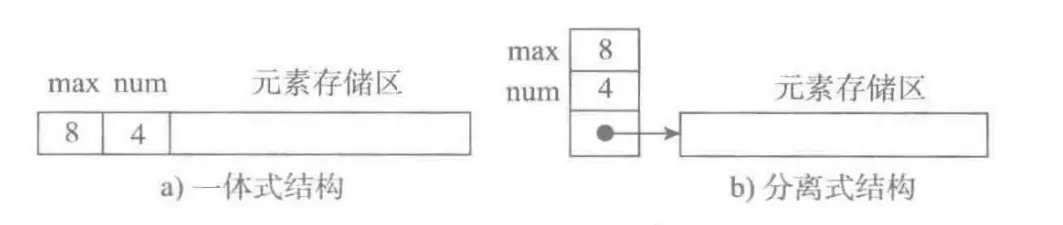
圖a	圖b
⼀體式結構,存儲表信息的單元與元素存儲區以連續的⽅式安排在⼀塊存儲區⾥，兩部分數據的整體形成⼀個完整的順序表對象	分離式結構，表對象⾥只保存與整個表有關的信息（即容量和元素個數），實際數據元素存放在另⼀個獨⽴的元素存儲區⾥，通過鏈接與基本表對象關聯。
⼀體式結構整體性強，易於管理。但是由於數據元素存儲區域是表對象的⼀部分，順序表創建後，元素存儲區就固定了

元素存儲區替換

⼀體式結構	分離式結構
由於順序表信息區與數據區連續存儲在⼀起，所以若想更換數據區，則只能整體搬遷，即整個順序表對象（指存儲順序表的結構信息的區域）改變了	若想更換數據區，只需將表信息區中的數據區鏈接地址更新即可，⽽該順序表對象不變

元素存儲區擴充

採⽤分離式結構的順序表，若將數據區更換為存儲空間更⼤的區域，則可以
在不改變表對象的前提下對其數據存儲區進⾏了擴充，所有使⽤這個表的地
⽅都不必修改，這種技術實現的順序表稱為動態順序表，因為其容量可以在使⽤中動態變化

擴充的兩種策略：

每次擴充增加固定數⽬	每次擴充容量加倍
每次擴充增加固定數⽬的存儲位置，如每次擴充增加10個元素位置，這種策略可稱為線性增⻓	每次擴充容量加倍，如每次擴充增加⼀倍存儲空間
特點：節省空間，但是擴充操作頻繁，操作次數多	特點：減少了擴充操作的執⾏次數，但可能會浪費空間資源。以空間換時間，推薦的⽅式

2.4.1.4、順序表的操作

增加元素：
a、尾端加⼊元素，時間複雜度為O(1)
b、保序的元素加⼊，時間複雜度為O(n)

刪除元素：
a、刪除表尾元素，時間複雜度為O(1)
b、保序的元素刪除，時間複雜度為O(n)

2.4.1.5、Python中的順序表

list和tuple兩種類型採⽤了順序表的實現技術，tuple是不可變類型，即不變的順序表，因此不⽀持改變其內部狀態的任何操作，⽽其他⽅⾯，則與list的性質類似

2.4.2、鏈表

1.定義
鏈表（Linked list）是⼀種常⻅的基礎數據結構，是⼀種線性表，但是不像順
序表⼀樣連續存儲數據，⽽是在每⼀個節點（數據存儲單元）⾥存放下⼀個
節點的位置信息（即地址）

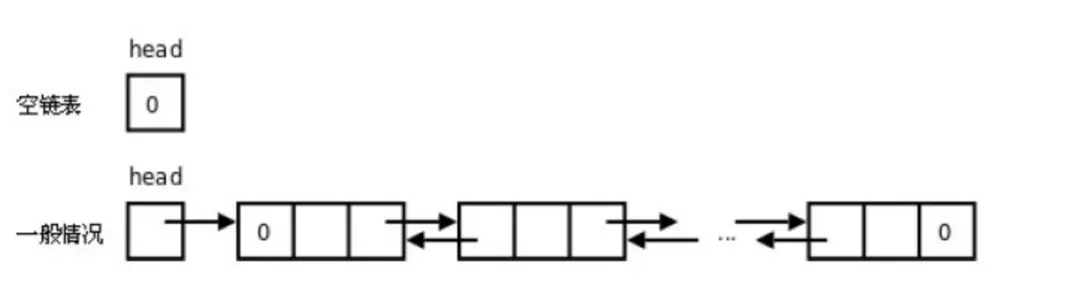
2.單向鏈表
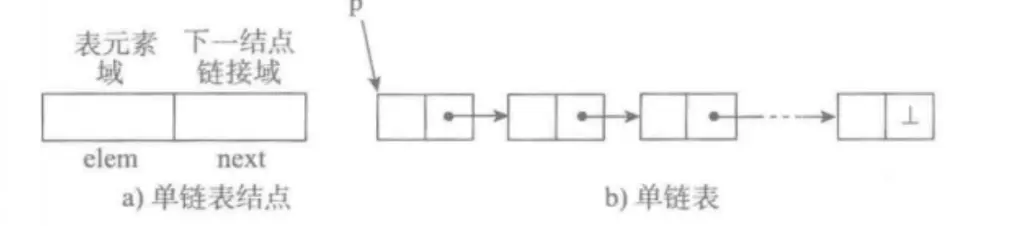
單向鏈表也叫單鏈表，是鏈表中最簡單的⼀種形式，它的每個節點包含兩個
域，⼀個信息域（元素域）和⼀個鏈接域。這個鏈接指向鏈表中的下⼀個節
點，⽽最後⼀個節點的鏈接域則指向⼀個空值

元素域elem⽤來存放具體的數據
鏈接域next⽤來存放下⼀個節點的位置（python中的標識）
變量p指向鏈表的頭節點（⾸節點）的位置，從p出發能找到表中的任意節點

3.節點的實現與節點的操作實現

class SingleNode(object):
    """
    單鏈表的節點實現
    """

    def __int__(self, item):
        self.item = item
        self.next = None


class SingleLinkList(object):
    """
    單鏈表的操作實現
    """

    def __init__(self):
        self.__head = None

    # 判斷鏈表為空
    def is_empty(self):
        return self.__head is None

    # 鏈表長度
    def length(self):
        cur = self.__head
        count = 0
        while cur is not None:
            count += 1
            cur = cur.next
        return count

    # 遍歷鏈表
    def travel(self):
        cur = self.__head
        while cur is not None:
            print(cur.item)
            cur = cur.next
        print("")

    # 頭部添加元素
    def add(self, item):
        node = SingleNode()
        node.item = item
        node.next = self.__head
        self.__head = node

    # 尾部添加元素
    def append(self, item):
        node = SingleNode()
        node.item = item
        if self.is_empty():
            self.__head = node
        else:
            cur = self.__head
            while cur.next is not None:
                cur = cur.next
            cur.next = node

    # 指定位置添加元素
    def insert(self, pos, item):
        if pos <= 0:
            self.add(item)
        elif pos >= self.length():
            self.append(item)
        else:
            cur = self.__head
            count = 0
            node = SingleNode()
            node.item = item
            while count < (pos - 1):
                count += 1
                cur = cur.next
            node.next = cur.next
            cur.next = node

    # 刪除元素
    def remove(self, item):
        cur = self.__head
        pre = None
        while cur is not None:
            if cur.item == item:
                if cur == self.__head:
                    self.__head = cur.next
                else:
                    pre.next = cur.next
                return
            pre = cur
            cur = cur.next

    # 查找元素
    def search(self, item):
        cur = self.__head
        while cur is not None:
            if cur.item == item:
                return True
            cur = cur.next
        return False

2.4.3、雙向鏈表

每個節點有兩個鏈接：⼀個指向前⼀個節點，當此節點為第⼀個節點時，指向空值；⽽另⼀個指向下⼀個節點，當此節點為最後⼀個節點時，指向空值

雙向鏈表實現與操作：

class DoubleNode(object):
    """
    雙向鏈表的節點實現
    """

    def __int__(self, item):
        self.item = item
        self.next = None
        self.pre = None


class DoubleLinkList(object):
    """
    雙向鏈表的操作實現
    """

    def __init__(self):
        self.__head = None

    # 判斷鏈表為空
    def is_empty(self):
        return self.__head is None

    # 鏈表長度
    def length(self):
        cur = self.__head
        count = 0
        while cur is not None:
            count += 1
            cur = cur.next
        return count

    # 遍歷鏈表
    def travel(self):
        cur = self.__head
        while cur is not None:
            print(cur.item)
            cur = cur.next
        print("")

    # 查找元素
    def search(self, item):
        cur = self.__head
        while cur is not None:
            if cur.item == item:
                return True
            cur = cur.next
        return False

    # 頭部添加元素
    def add(self, item):
        node = DoubleNode()
        node.item = item
        node.next = self.__head
        self.__head = node
        if node.next:
            node.next.pre = node

    # 尾部添加元素
    def append(self, item):
        node = DoubleNode()
        node.item = item
        if self.is_empty():
            self.__head = node
        else:
            cur = self.__head
            while cur.next is not None:
                cur = cur.next
            node.pre = cur
            cur.next = node

    # 指定位置添加元素
    def insert(self, pos, item):
        if pos <= 0:
            self.add(item)
        elif pos >= self.length():
            self.append(item)
        else:
            cur = self.__head
            count = 0
            node = DoubleNode()
            node.item = item
            while count < pos:
                count += 1
                cur = cur.next
            node.next = cur
            node.pre = cur.pre
            cur.pre.next = node
            cur.pre = node

    # 刪除元素
    def remove(self, item):
        cur = self.__head
        while cur is not None:
            if cur.item == item:
                if cur == self.__head:
                    self.__head = cur.next
                    if cur.next:
                        self.__head.pre = None
                else:
                    cur.pre.next = cur.next
                    if cur.next:
                        cur.next.pre = cur.pre
                return
            cur = cur.next

2.4.4、單向循環鏈表

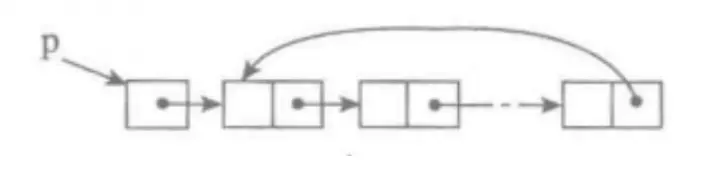
單鏈表的⼀個變形是單向循環鏈表，鏈表中最後⼀個節點的next域不再為
None，⽽是指向鏈表的頭節點

單向循環鏈表的實習與操作實現：

class SingleNode(object):
    """
    單向循環鏈表的節點實現
    """

    def __int__(self, item):
        self.item = item
        self.next = None


class SingleLinkList(object):
    """
    單向循環鏈表的操作實現
    """

    def __init__(self):
        self.__head = None

    # 判斷鏈表為空
    def is_empty(self):
        return self.__head is None

    # 鏈表長度
    def length(self):
        if self.is_empty():
            return 0
        cur = self.__head
        count = 1
        while cur.next != self.__head:
            count += 1
            cur = cur.next
        return count

    # 遍歷鏈表
    def travel(self):
        if self.is_empty():
            print("")
            return
        cur = self.__head
        while cur.next != self.__head:
            print(cur.item)
            cur = cur.next
        print(cur.item)

    # 頭部添加元素
    def add(self, item):
        node = SingleNode()
        node.item = item
        if self.is_empty():
            self.__head = node
            node.next = node
        cur = self.__head
        while cur.next != self.__head:
            cur = cur.next
        node.next = self.__head
        self.__head = node
        cur.next = self.__head

    # 尾部添加元素
    def append(self, item):
        node = SingleNode()
        node.item = item
        if self.is_empty():
            self.__head = node
            node.next = node
        else:
            cur = self.__head
            while cur.next != self.__head:
                cur = cur.next
            cur.next = node
            node.next = self.__head

    # 指定位置添加元素
    def insert(self, pos, item):
        if pos <= 0:
            self.add(item)
        elif pos >= self.length():
            self.append(item)
        else:
            cur = self.__head
            count = 0
            node = SingleNode()
            node.item = item
            while count < (pos - 1):
                count += 1
                cur = cur.next
            node.next = cur.next
            cur.next = node

    # 刪除元素
    def remove(self, item):
        if self.is_empty():
            return
        cur = self.__head
        pre = None
        while cur.next != self.__head:
            if cur.item == item:
                if cur == self.__head:
                    rear = self.__head
                    while rear.next != self.__head:
                        rear = rear.next
                    self.__head = cur.next
                    rear.next = self.__head
                else:
                    pre.next = cur.next
                return
            pre = cur
            cur = cur.next
        if cur.item == item:
            if cur == self.__head:
                self.__head = None
            else:
                pre.next = self.__head

    # 查找元素
    def search(self, item):
        if self.is_empty():
            return False
        cur = self.__head
        while cur.next != self.__head:
            if cur.item == item:
                return True
            cur = cur.next
        if cur.item == item:
            return True
        return False

2.4.5、棧

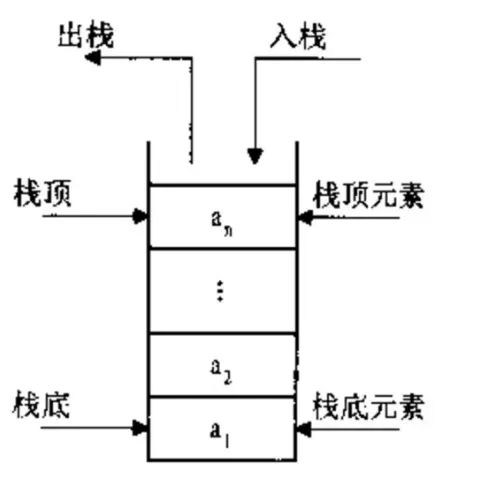
棧（stack），也稱為堆棧，是⼀種容器，可存⼊數據元素、訪問元素、刪除元素，它的特點在於只能允許在容器的⼀端（稱為棧頂端指標，英語：top）進⾏加⼊數據（英語：push）和輸出數據（英語：pop）的運算。
由於棧數據結構只允許在⼀端進⾏操作，因⽽按照後進先出（LIFO, Last In First Out）的原理運作。

棧結構實現：可以⽤順序表實現，也可以⽤鏈表實現
棧的操作：

class Stack(object):
    def __init__(self):
        self.__items = []

    # 空
    def is_empty(self):
        return self.__items == []

    # 添加元素到棧頂
    def push(self, item):
        self.__items.append(item)

    # 取元素
    def pop(self):
        return self.__items.pop()

    # 返回棧頂元素
    def peek(self):
        return self.__items[-1]

    # 返回棧的長度
    def size(self):
        return len(self.__items)

2.4.6、隊列

隊列（queue）是隻允許在⼀端進⾏插⼊操作，⽽在另⼀端進⾏刪除操作的線性表。
隊列是⼀種先進先出的（First In First Out）的線性表，簡稱FIFO。允許插⼊
的⼀端為隊尾，允許刪除的⼀端為隊頭。隊列不允許在中間部位進⾏操作！
假設隊列是q=（a1，a2，……，an），那麼a1就是隊頭元素，⽽an是隊尾
元素。這樣我們就可以刪除時，總是從a1開始，⽽插⼊時，總是在隊列最
後。這也⽐較符合我們通常⽣活中的習慣，排在第⼀個的優先出列，最後來
的當然排在隊伍最後。

隊列操作：

class Queue(object):
    """隊列"""

    def __init__(self):
        self.items = []

    def is_empty(self):
        return self.items == []

    def enqueue(self, item):
        """進隊列"""
        self.items.insert(0, item)

    def dequeue(self):
        """出隊列"""
        return self.items.pop()

    def size(self):
        """返回⼤⼩"""
        return len(self.items)

2.4.7、雙端隊列

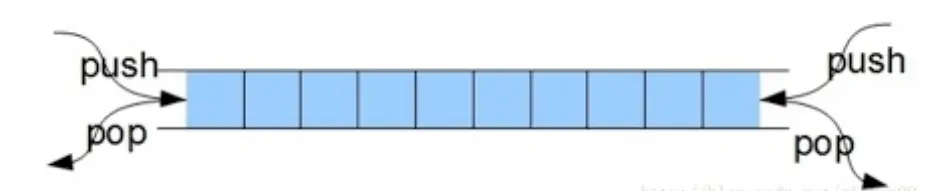
雙端隊列（deque，全名double-ended queue），是⼀種具有隊列和棧的性質的數據結構。
雙端隊列中的元素可以從兩端彈出，其限定插⼊和刪除操作在表的兩端進⾏。
雙端隊列可以在隊列任意⼀端⼊隊和出隊

棧 , 鏈表 , 隊列 , 雙向鏈表 , 數據結構和算法

測試菜鳥 Blog

@wenroudemangguo

Tags

數據結構和算法 (25)

隊列 (24)

棧 (7)

鏈表 (7)

雙向鏈表 (1)