此分類用於記錄吳恩達深度學習課程的學習筆記。
課程相關信息鏈接如下:
- 原課程視頻鏈接:[雙語字幕]吳恩達深度學習deeplearning.ai
- github課程資料,含課件與筆記:吳恩達深度學習教學資料
- 課程配套練習(中英)與答案:吳恩達深度學習課後習題與答案
本篇為第二課第一週的內容,1.9的內容。
本週為第二課的第一週內容,就像課題名稱一樣,本週更偏向於深度學習實踐中出現的問題和概念,在有了第一課的機器學習和數學基礎後,可以説,在理解上對本週的內容不會存在什麼難度。
當然,我也會對一些新出現的概念補充一些基礎內容來幫助理解,在有之前基礎的情況下,按部就班即可對本週內容有較好的掌握。
在學習完一些緩解過擬合的方法後,我們便可以較好的訓練神經網絡,而不至於出現因為模型複雜度上升反而導致模型性能下降的情況。
這樣,神經網絡就可以較好的擬合數據。
而這一部分的內容,就是在這個基礎上如何加快神經網絡的訓練,實現更快,更穩定地收斂。
1.歸一化
還是先把概念擺出來:
歸一化(Normalization)是指將數據按一定的比例或標準進行調整,使得數據的數值範圍或分佈符合某種特定的要求。通常,歸一化的目標是將數據轉化為統一的尺度,便於不同數據之間的比較或用於某些算法中。
要提前説明的是,下面的筆記內容介紹的只是歸一化方法中最普適的一種,叫Z-Score標準化(標準差標準化),也可以直接叫標準化。
1.1 標準化的步驟
(1)計算樣本的均值
對每一維特徵,計算其均值 \(\mu\) 。
我們用一組數據在每一步進行相應處理來演示這個完整的過程:
原始樣本:\([10, 12, 9, 15, 14]\),樣本數 \(N=5\)
(2)計算每個樣本與均值的差 \((x - \mu)\) 以及平方差
| 樣本 \(x\) | \(x - \mu\) | \((x - \mu)^2\) |
|---|---|---|
| 10 | -2 | 4 |
| 12 | 0 | 0 |
| 9 | -3 | 9 |
| 15 | 3 | 9 |
| 14 | 2 | 4 |
(3)計算方差與標準差
總體方差(分母使用 \(N\)):
總體標準差:
(4)執行標準化變換
每個樣本的標準化結果:
逐項計算:
| \(x\) | \(x-\mu\) | \(z = \frac{x-\mu}{\sigma}\) |
|---|---|---|
| 10 | -2 | -0.877058 |
| 12 | 0 | 0.000000 |
| 9 | -3 | -1.315587 |
| 15 | 3 | 1.315587 |
| 14 | 2 | 0.877058 |
因此標準化後的結果為:
這樣,我們就對數據完成了一次標準化,那進行這些步驟的作用又是什麼呢?
1.2標準化的作用
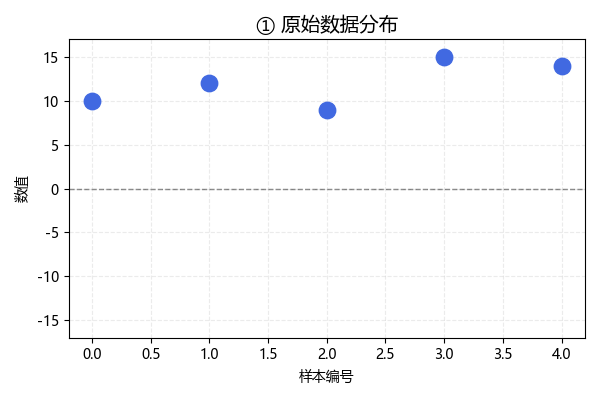
我們來看一下各個步驟後,樣本數據的變化:
這是未經處理的原始數據,現在,我們按照標準化公式一步步進行:
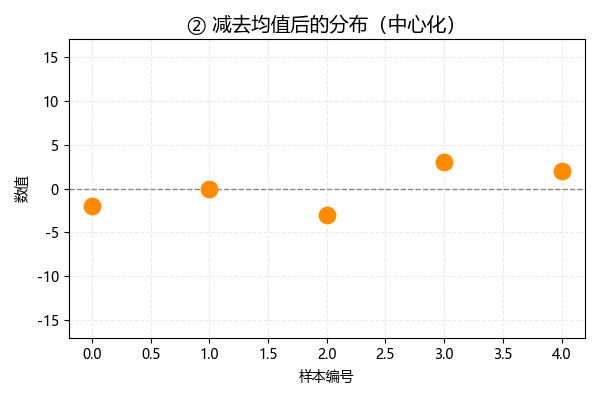
將各數據減去均值,這一步也叫做中心化,此時數據分佈如下:
可以發現,中心化後,數據的均值變為 0:
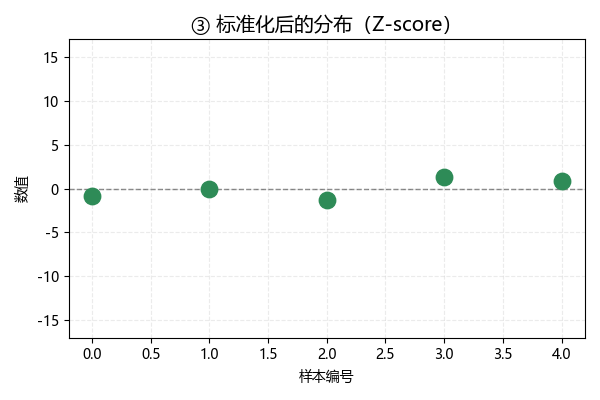
現在,我們再把中心化的數據除以標準差,此時數據分佈如下:
經過這一步,標準化後數據的標準差為 1:
也就是説,標準化後,數據的均值變為0,標準差變為1,這是它的作用,可這樣的變換又是如何幫助訓練的呢?
我們繼續下一節。
1.3 標準化如何幫助訓練?
(1)消除量綱差距的同時保持特徵信息
在現實數據中,不同特徵往往有不同的單位或數量級。
例如,在一個房價預測模型中:
- 房屋面積以“平方米”計,數值可能在幾十到幾百;
- 房間數量只在“1~5”之間變化。
如果不做標準化,面積特徵的值遠大於房間數,模型在更新參數時會更偏向面積,而忽視房間數量的影響。
對此,標準化這樣解決這個問題:
- 中心化:將每個特徵的均值移動到 0,使數據以 0 為中心,正負對稱,方便神經網絡處理。
- 除以標準差:標準差就像一個“伸縮尺”,根據特徵自身的波動範圍對數據進行拉伸或壓縮,波動大的特徵被壓縮幅度大,波動小的特徵被壓縮幅度小,從而統一特徵尺度。
要説明的是,除以標準差精妙的地方在於統一尺度的同時保留了同一特徵內的差距。
舉個例子:
對於兩個人的年齡,一個人20歲,一個人10歲。
壓縮後,前一個人變成了2歲,後一個人變成了1歲。
但是他們之間的差別關係沒有變化,前者仍比後者大,我們只是把跨度從10歲縮小從了1歲來減少波動性。模型依舊可以區分兩個樣本的差別。
我們再用房屋的實例説明來整體演示一下:
- 設房屋面積原始值:[50, 120, 200, 300, 400], 房間數原始值:[1, 2, 3, 4, 5]
- 中心化後:面積:[−167, −97, −17, 83, 183],房間數:[−2, −1, 0, 1, 2]
- 除以標準差(面積 σ≈145.44,房間數 σ≈1.414)後: 面積標準化:[−1.15, −0.67, −0.12, 0.57, 1.26], 房間數標準化:[−1.41, −0.71, 0, 0.71, 1.41]
這樣,通過標準化,面積和房間數都被縮放到大致相似的範圍,梯度更新時影響力平衡,同時保持了各房屋之間的相對差異。
可以形象地理解為:每個特徵都被配上了“統一的尺子”,讓它們在同一尺度下公平競爭,既消除了量綱差距,又保持原始信息。
(2)平衡含正負值的數據集
標準化後的數據以 0 為中心,分佈更對稱,特別適合使用如 tanh、ReLU 等激活函數的神經網絡。
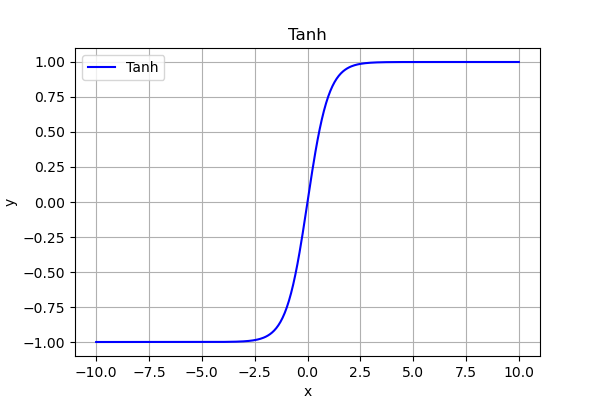
我們用tanh舉例:
如果輸入特徵全是正數,tanh 的輸出始終偏向 1 區域,梯度幾乎為 0,學習停滯。
而經過標準化後,輸入既有正又有負,輸出能覆蓋整個區間,梯度保持活躍,網絡學習更充分。
這便是關於歸一化的內容,下一篇便是本週理論部分的最後一篇,是關於網絡運行中一些常見的梯度現象和其應對方法。