此分類用於記錄吳恩達深度學習課程的學習筆記。
課程相關信息鏈接如下:
- 原課程視頻鏈接:[雙語字幕]吳恩達深度學習deeplearning.ai
- github課程資料,含課件與筆記:吳恩達深度學習教學資料
- 課程配套練習(中英)與答案:吳恩達深度學習課後習題與答案
本篇為第五課的第一週內容,1.2到1.4的內容。
本週為第五課的第一週內容,與 CV 相對應的,這一課所有內容的中心只有一個:自然語言處理(Natural Language Processing,NLP)。
應用在深度學習裏,它是專門用來進行文本與序列信息建模的模型和技術,本質上是在全連接網絡與統計語言模型基礎上的一次“結構化特化”,也是人工智能中最貼近人類思維表達方式的重要研究方向之一。
這一整節課同樣涉及大量需要反覆消化的內容,橫跨機器學習、概率統計、線性代數以及語言學直覺。
語言不像圖像那樣“直觀可見”,更多是抽象符號與上下文關係的組合,因此理解門檻反而更高。
因此,我同樣會儘量補足必要的背景知識,儘可能用比喻和實例降低理解難度。
本篇的內容關於循環神經網絡,在 NLP 中,循環神經網絡就像卷積網絡在 CV 中一樣,是處理序列數據的核心特化模型,專門用於捕捉上下文依賴。
1. NLP 中的符號規範
在正式開始引入循環神經網絡前,我們同樣需要先了解一些相關的符號規範,主要是在數據的表示方面。
1.1 模型的輸入與輸出

再複述一下:
- \(x^{<t>}\) :輸入序列在第 \(t\) 個時間步的輸入。
- \(y^{<t>}\) :輸出序列在第 \(t\) 個時間步的輸出。
- \(T_x\):輸入序列的長度。
- \(T_y\):輸出序列的長度。
現在,結合我們之前的符號規範,就可以知道:
\(X^{(n)<t>}\) 代表一批次輸入中第 \(n\) 個樣本的第 \(t\) 個元素。
1.2 詞典(Vocabulary)
經過上一部分,我們知道,\(x^{<t>}\) 代表了一個序列中的某一個元素。
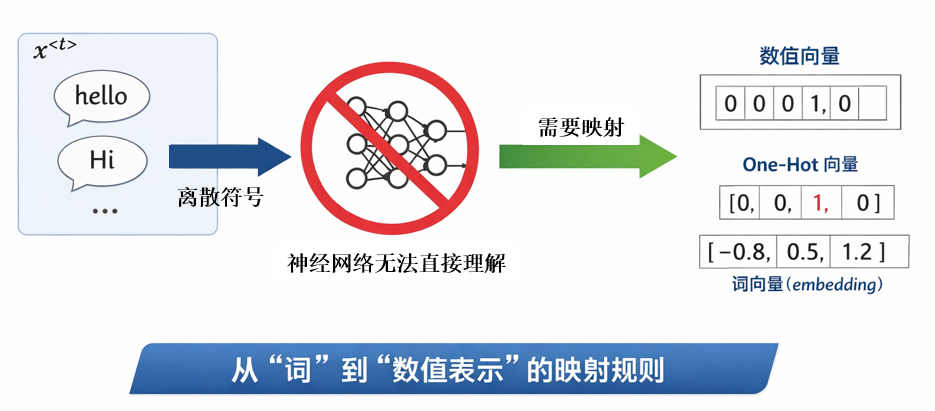
但是又有一個新的問題:在 NLP 任務中,\(x^{<t>}\) 往往是一個離散的符號,例如某個具體的詞(如 hello、Hi),而神經網絡本質上只能處理數值向量,並不能直接理解“詞”這一抽象概念。
因此,在將文本序列送入模型之前,我們必須先完成一件事情:給“詞”一個能輸入網絡的表示方法,即建立一種從“詞”到“數值表示”的映射規則。
顯然,這種映射關係必須是確定且唯一的,即每一個詞都對應一個唯一的數值表示。
而其中一種表示方法,就是我們在多分類標籤表示中使用的獨熱編碼。
我們看一個簡單的示例:
假設我們當前的詞典只包含 4 個詞:
我們可以為詞典中的每一個詞分配一個唯一的索引:
在這種設定下,每一個詞都可以用一個長度為 4 的獨熱向量來表示。
例如:
- \(\text{hello}\) 對應的表示為:\(x = [1,0,0,0]\)
- \(\text{Hi}\) 對應的表示為:\(x = [0,1,0,0]\)
詞典中的每個詞都有且僅有一個位置為 1,其餘位置全部為 0。
從模型的角度來看,這樣的表示方式意味着:模型在任意時刻接收到的輸入,本質上是一個高維稀疏向量,這正好滿足“詞 → 數值向量”的一對一映射要求,因此能夠直接作為神經網絡的輸入。
然而,在真實的 NLP 任務中,一個不可忽視的現實問題是:詞典的規模通常非常巨大。
在常見的語言建模或翻譯任務中,詞典大小往往達到數萬甚至百萬級別。
這意味着:
- 獨熱向量的維度極高
- 向量極度稀疏
- 計算和存儲成本都非常不經濟
因此,在實際模型中,我們往往會採用一種更緊湊、也更具語義表達能力的詞表示方法,叫做詞向量(Embedding) ,我們會在之後的內容詳細展開它。
此外,還會出現另一個問題: 測試或實際使用時,可能會遇到詞典中從未出現過的詞。
對於這種不在詞典中的詞(Out-Of-Vocabulary,OOV),常見的一種處理方式是在詞典中額外引入一個特殊標記<UNK>,用於統一表示所有未知詞,這種方式雖然簡單,但也會丟失不同未知詞之間的差異性,這也是後續子詞建模方法要解決的問題之一。
這些我們都會在之後的實際演示中詳細展開,現在,先了解簡單的符號規範後,我們正式開始引入循環神經網絡。
2. 循環神經網絡(Recurrent Neural Network,RNN)
在上一篇對序列模型的介紹中,我們已經知道:全連接網絡和卷積網絡並不適合用來處理序列數據。
我們需要一種模型,在處理當前輸入的同時,能夠保留並更新對“過去信息”的表示,讓模型在理解當前內容時,不是孤立地“看這一刻”,而是基於整個上下文來判斷。
而這,就是 RNN 的基本思想。
RNN最早可追溯到 Jordan(1986)對序列連接主義模型的研究,而現代深度學習中常用的 RNN 基本形式,則來源於 Elman 在1990年發表的一篇論文: Finding Structure in Time中提出的遞歸狀態網絡結構。
可以看到,儘管論文距今已有幾十年,但像最初的 CNN 一樣,RNN 的思想並沒有被時間淹沒,而是不斷被推廣和創新,最終成為現代 NLP 中不可或缺的基礎模型。
現在,我們用一個最簡單的單層循環神經網絡來介紹 RNN 的傳播過程及其特點。
2.1 單層循環神經網絡的結構
來看課程裏這樣一個循環網絡的傳播示意圖:
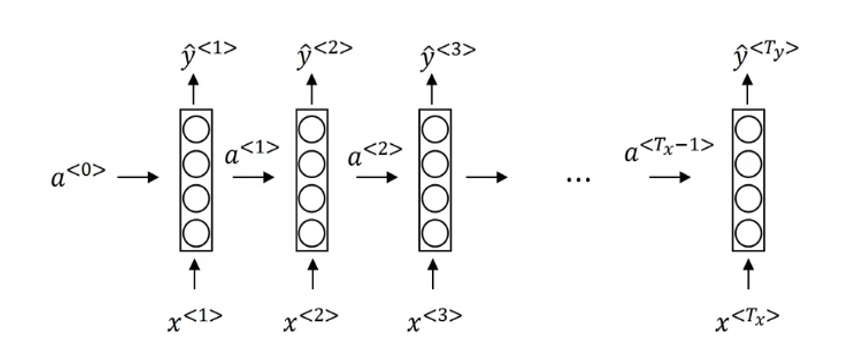
你可能會覺得,這個結構看起來好像不像傳統意義上的“單層網絡”,反而更像每一層都直接接收原始輸入的全連接網絡。
其實這正體現了 RNN 與 FN 或 CNN 的本質區別:在 RNN 中,每個時間步的隱藏狀態不會直接傳給下一層,而是傳遞給下一個時間步的自身。
也就是説,這個網絡的實際結構是這樣的:
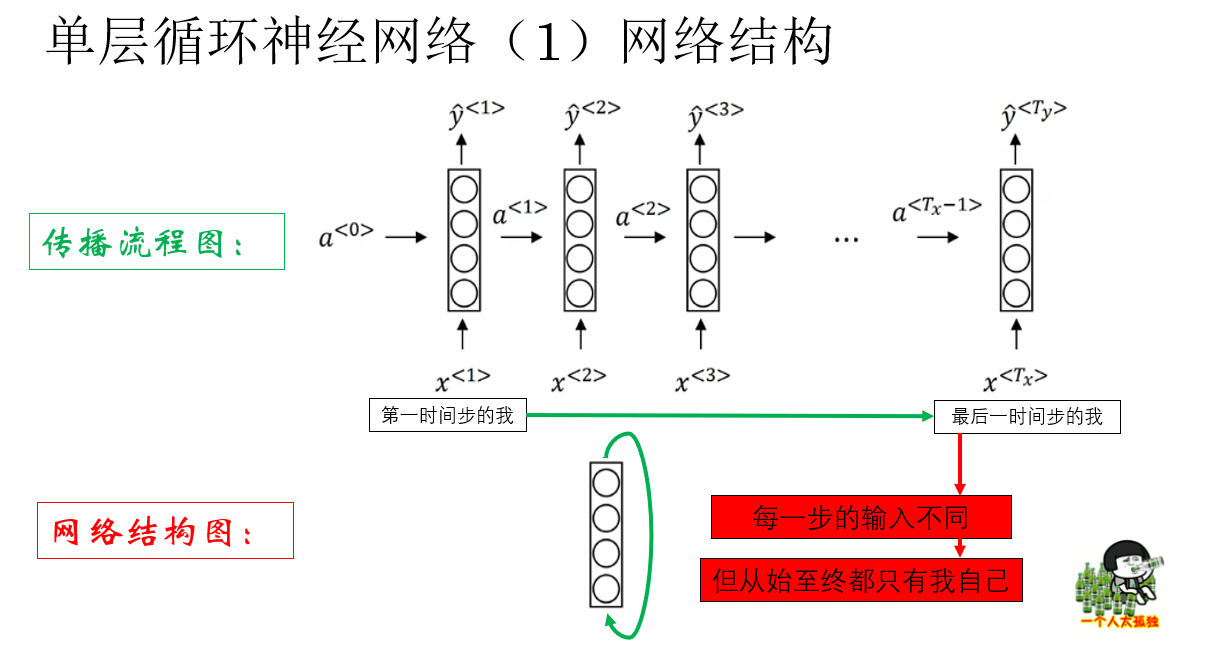
也就是説,RNN 本質上就是在全連接層基礎上加了時間維度的循環連接。
你會發現,如果拋開傳播邏輯不看,單層循環網絡實際上就是一層全連接層。
但這也恰恰説明了它的傳播邏輯的重要性,到底是怎麼樣的設計能讓單層的全連接層一躍而成為 NLP 的基石?
我們繼續。
2.2 單層循環神經網絡的正向傳播
瞭解了 RNN 的基本邏輯後, 現在,我們就來演示一下單層 RNN 的具體傳播過程中的一些細節:
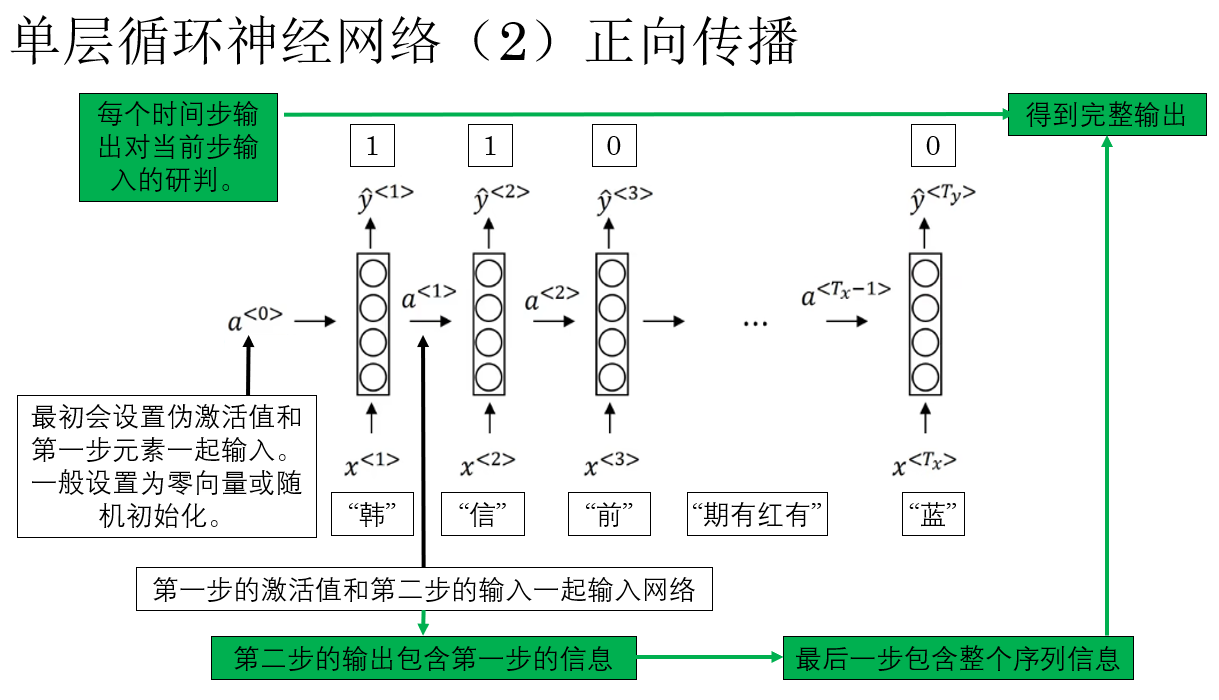
瞭解了這些後,我們規範一下單層 RNN 的正向傳播過程:
- 初始狀態
RNN 在第一個時間步輸入第一個元素 \(x^{<1>}\)(例如“韓”)時,同時會引入初始的偽激活值 (\(a^{<0>}\)) 作為網絡的初始狀態,\(a^{<0>}\) 通常設為零向量或隨機初始化。 - 逐步處理序列
每個時間步,RNN 會將當前輸入 \(x^{<t>}\) 與上一時間步的隱藏狀態 \(a^{<t-1>}\) 一起輸入網絡,計算當前的隱藏狀態 \(a^{<t>}\),例如在第二步,輸入為 \(x^{<2>}\)(“信”)和 \(a^{<1>}\),得到 \(a^{<2>}\)。 - 輸出生成
每一步的隱藏狀態 \(a^{<t>}\) 都會產生一個預測輸出 \(\hat{y}^{<t>}\)。輸出不僅依賴當前輸入,也包含了前面時間步的歷史信息,這就是 RNN 能夠“記憶”序列上下文的原因。 - 信息傳遞
隱藏狀態會沿時間步向後傳遞,使後續時間步的輸出能夠利用之前所有的序列信息,最終一步輸出 \(\hat{y}^{<T_x>}\) 包含整個序列的信息,可用於完整序列的預測或判斷。
明白了傳播邏輯後,我們便可以更好地理解 RNN 正向傳播的公式表達,我們先説明一下網絡中的參數表示:
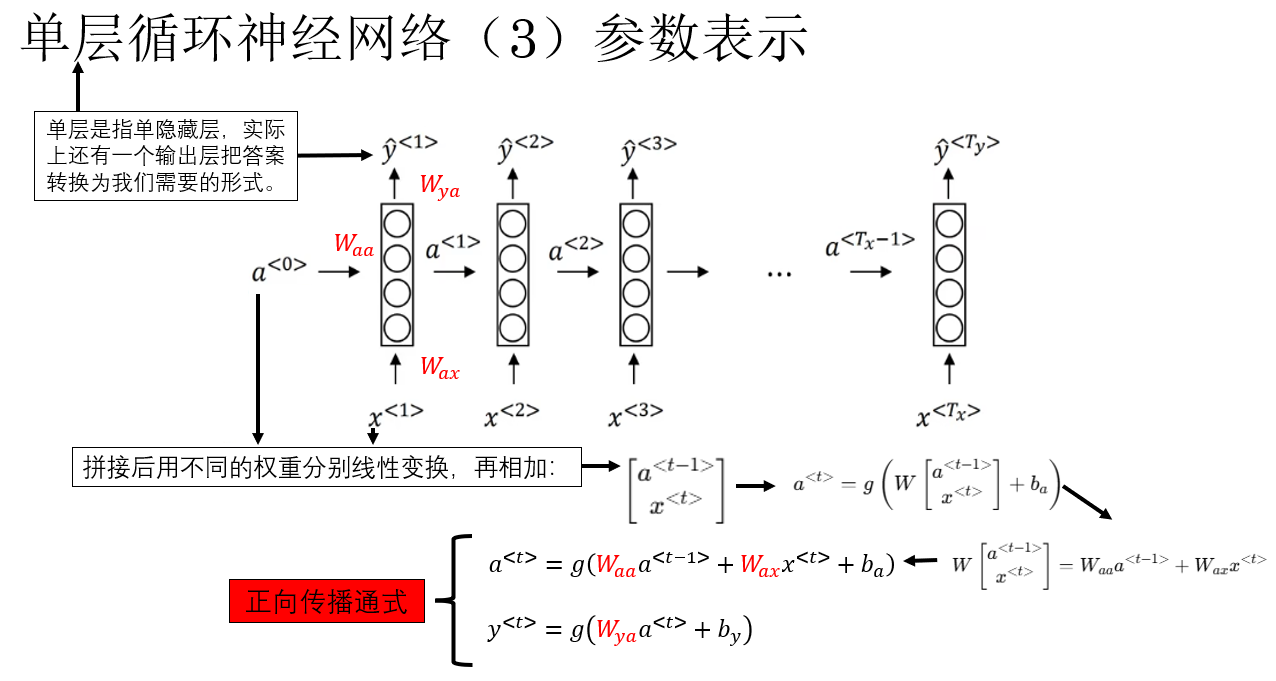
現在便擺出正向傳播的通式如下:
總結一下:RNN 的正向傳播就是每個時間步將當前輸入和上一隱藏狀態結合,更新當前隱藏狀態並生成輸出,隱藏狀態沿時間步傳遞,從而使網絡能夠逐步累積和利用序列歷史信息。
瞭解了正向傳播的大致流程後,我們再看看 RNN 的反向傳播是如何進行的。
2.3 單層循環神經網絡的反向傳播
經過上一部分,我們已經知道:RNN 的正向傳播,本質上是在時間維度上反覆使用同一組參數,並通過隱藏狀態把歷史信息向後傳遞。
那麼問題自然就來了: 這些跨時間步傳遞的信息,反向傳播時該怎麼“算梯度”?
答案是: 怎麼過去就怎麼回來——RNN 的反向傳播,並不是在“層”之間傳播,而是在時間維度上反向傳播,這種傳播被稱為 BPTT(Backpropagation Through Time) 。
我們來簡要演示一下這個過程:
在監督學習中,反向傳播的起點永遠是損失函數,對於 RNN 來説,損失通常是所有時間步損失的累加(默認 \(T_x = T_y\)):
也就是説,每一個時間步的輸出都會對總損失產生貢獻。
而對於單步的損失,最常用的仍然是我們比較熟悉的交叉熵損失,你可以通過鏈接查看我們之前的介紹,應用在 RNN 中,它的公式是這樣的:
因此,反向傳播時,我們會從最後一個時間步開始,逐步向前,把每個時間步的誤差信號往回傳, 由於參數在所有時間步共享,每個時間步的損失都會通過時間鏈路對這些參數產生梯度貢獻,最終用於更新的梯度,是沿時間維度反向傳播後,各時間步貢獻的綜合結果。
這就是單層循環神經網絡的反向傳播,這樣我們就對 RNN 的基本運行邏輯有了大體的瞭解。
3.總結
| 概念 | 原理 | 比喻 |
|---|---|---|
| 序列數據 | 數據元素具有明確順序,當前理解依賴歷史上下文 | 一句話的意思要從前往後讀,不能只看中間一個詞。 |
| 時間步 \(t\) | 序列中第 \(t\) 個位置,用於展開時間維度 | 時間軸上的第 \(t\) 幀畫面。 |
| 輸入 \(x^{}\) | 第 \(t\) 個時間步送入模型的輸入向量 | 當前這一秒你聽到的一個詞。 |
| 預測輸出 \(\hat{y}^{}\) | 模型在第 \(t\) 個時間步給出的預測結果 | 聽到一句話後,此刻你做出的判斷。 |
| 序列長度 \(T_x, T_y\) | 輸入序列與輸出序列的長度(可相同或不同) | 一段話的字數 vs 你回答時説了幾句話。 |
| 詞典(Vocabulary) | 從詞到索引的一一映射表 | 電話簿:名字 ↔ 電話號碼 |
| RNN 核心思想 | 當前狀態由當前輸入 + 過去狀態共同決定 | 你理解一句話時,會不斷修正之前的理解。 |
| BPTT | 梯度沿時間維度反向傳播 | 從句尾倒回去反思:是哪一步理解錯了。 |
| 梯度累積 | 參數梯度來自所有時間步的綜合貢獻 | 每一句話的錯誤都會影響你下次的理解方式。 |
。


