此分類用於記錄吳恩達深度學習課程的學習筆記。
課程相關信息鏈接如下:
- 原課程視頻鏈接:[雙語字幕]吳恩達深度學習deeplearning.ai
- github課程資料,含課件與筆記:吳恩達深度學習教學資料
- 課程配套練習(中英)與答案:吳恩達深度學習課後習題與答案
本篇為第五課的第一週內容,1.9的內容以及一些相關基礎的補充。
本週為第五課的第一週內容,與 CV 相對應的,這一課所有內容的中心只有一個:自然語言處理(Natural Language Processing,NLP)。
應用在深度學習裏,它是專門用來進行文本與序列信息建模的模型和技術,本質上是在全連接網絡與統計語言模型基礎上的一次“結構化特化”,也是人工智能中最貼近人類思維表達方式的重要研究方向之一。
這一整節課同樣涉及大量需要反覆消化的內容,橫跨機器學習、概率統計、線性代數以及語言學直覺。
語言不像圖像那樣“直觀可見”,更多是抽象符號與上下文關係的組合,因此理解門檻反而更高。
因此,我同樣會儘量補足必要的背景知識,儘可能用比喻和實例降低理解難度。
本篇的內容關於門控循環單元 GRU,它通過改變 RNN 的隱藏層,來緩解 RNN 的梯度消失問題。
1. 什麼是 GRU(Gated Recurrent Unit)?
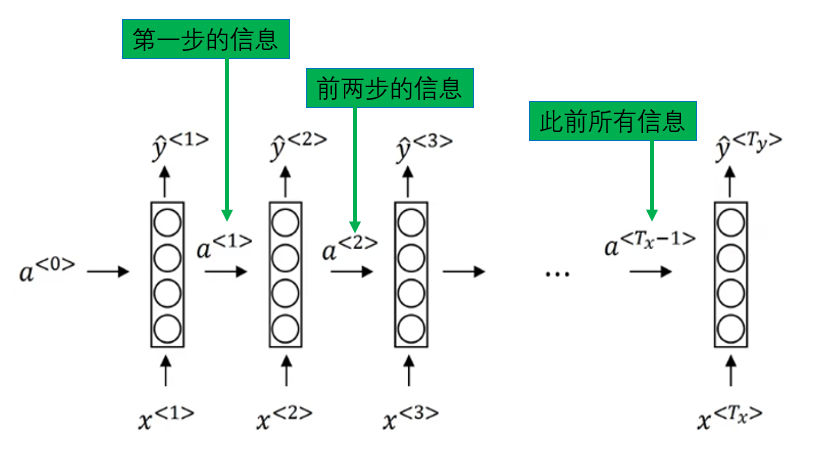
在前面的內容裏中我們已經提到過:RNN 的核心機制,是把歷史信息壓縮進一個不斷傳遞的隱藏狀態中。
結果就是我們已經分析過的結論:信息一旦隔得太遠,就會在反覆的線性變換和非線性映射中被不斷稀釋。
在反向傳播時就體現為梯度越來越小,最終幾乎傳不回去,導致“開頭被遺忘”,這就是 RNN 的長距離依賴問題。
顯然,這並不是改善訓練技巧可以解決的問題,而是 RNN 本身的結構造成的限制,自然而然地就引出了 NLP 領域的新問題 :如何緩解 RNN 的長距離依賴問題? 即如何讓模型“記得更久一些”?
於是,在 2014 年發表的一篇論文: On the Properties of Neural Machine Translation: Encoder–Decoder Approaches 中,提出了一種帶有門控機制的循環單元結構,即後來被稱為 GRU(Gated Recurrent Unit) 的模型。
該工作首次在 Encoder–Decoder 框架下系統性地引入 “更新門”和“重置門”,通過對隱藏狀態的信息流進行選擇性控制,從結構層面緩解了傳統 RNN 在長序列建模中面臨的困難。
同年的另一篇論文:Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling 對其實際效果進行了系統評估。實驗結果證明了其優越的性能,這也使其迅速成為實際 NLP 系統中廣泛採用的基礎循環單元之一。
出現了很多沒見過的名詞,別擔心,下面我們就來詳細展開。
1.1 GRU 的解題思路
首先,面對”如何讓模型記得更久一些”的問題,GRU給出的答案是:
既然記不住全部,那我能不能只記重要的?
這是什麼意思?回憶一下 普通 RNN 是如何進行記憶的:
我們已經很熟悉這個過程了:
但是,實際上,在真實語言中,我們並不是這樣處理信息的。
舉個例子:
“我昨天去北京出差,
在路上遇到了一個多年未見的朋友,
他現在在……”
當你看到“他”的時候:
- 你不需要記住“北京”,“昨天”。
- 但你必須記住“朋友”。
- 換句話説,當前時刻的理解,並不依賴於全部歷史內容,而只依賴於與當前判斷相關的信息。
再概括來講,人腦在處理序列信息時,隱含着一個非常重要的能力:選擇性記憶。
而 GRU 的設計,正是將這種“取捨能力”,通過門控結構的形式,顯式地引入到 RNN 的隱藏層更新過程中。
簡單展開一下,GRU 並沒有改變 RNN 的整體框架:
- 仍然是時間步 \(t = 1, 2, \dots\)
- 仍然有輸入 \(x^{<t>}\)
- 仍然有隱藏狀態 \(a^{<t>}\)
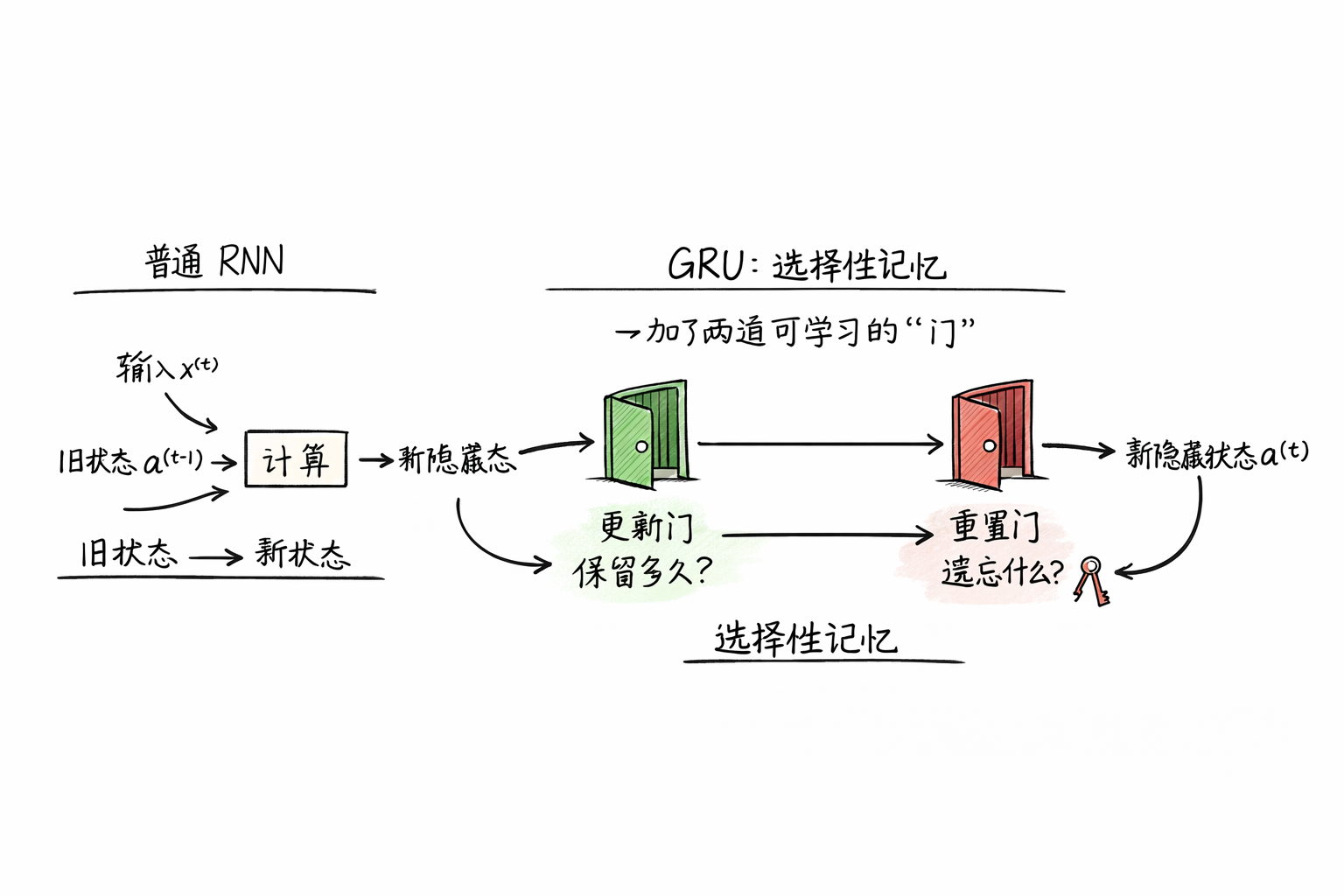
它真正改變的,只有一件事:在“舊狀態 → 新狀態”的過程中,加了兩道可學習的“門”。 就是我們下面要説的 “更新門”和“重置門”。
1.2 GRU 的更新門(Update Gate)
第一道門,叫 更新門(Update Gate)。
它負責回答的問題是:
“當前這一步,我要保留多少過去的記憶?”
也就是説:
- 更新門開得越大 → 舊狀態保留得越多
- 更新門關得越緊 → 當前輸入對隱藏狀態的影響越大
總結來説,更新門衡量的是:“這條歷史信息,值不值得繼續往後傳?”
這一設計直接解決了 RNN 的一個問題:普通 RNN 每一步都會用新輸入強行覆蓋舊隱藏狀態,
長期信息容易被逐步稀釋,而更新門讓模型可以選擇性保留重要歷史信息。
我們回到之前的例子:
“我昨天去北京出差,
在路上遇到了一個多年未見的朋友,
他現在在……”
在生成“他”對應的隱藏狀態時:
- 更新門會讓模型保留“朋友”這個關鍵信息,因為它對理解代詞至關重要
- 同時,更新門會削弱“昨天”“北京”等不相關信息的影響
於是,通過更新門,模型可以自動判斷哪些歷史值得繼續傳遞,哪些可以淡化。
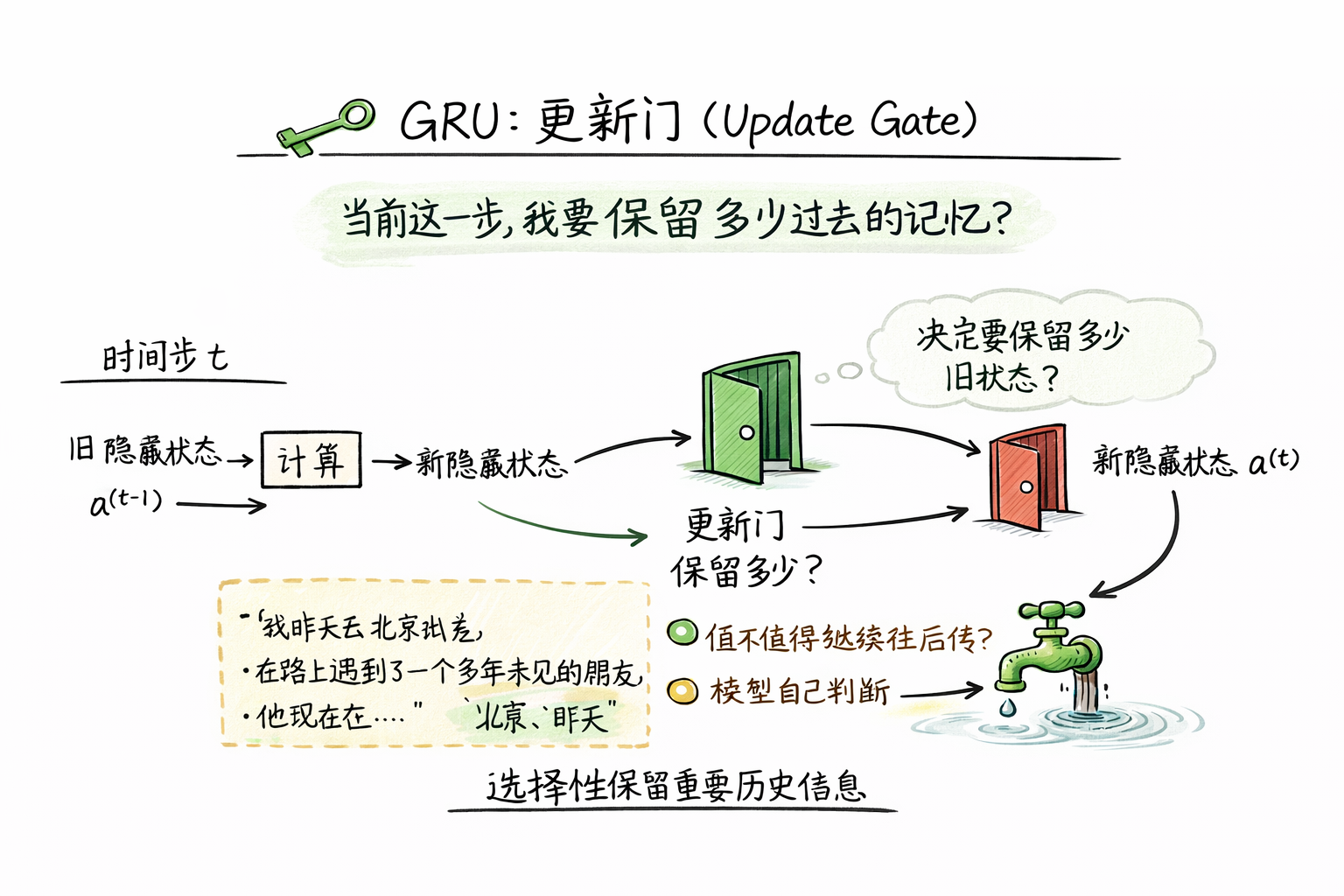
其實,這種思路和我們之前在優化算法部分介紹的 指數加權平均 很相似:舊狀態像過去的平均值,更新門控制“平均時的新權重”,讓重要信息得到保留。
1.3 GRU 的重置門(Reset Gate)
第二道門,叫 重置門(Reset Gate)。
它關心的不是“保留多少舊信息”,而是:
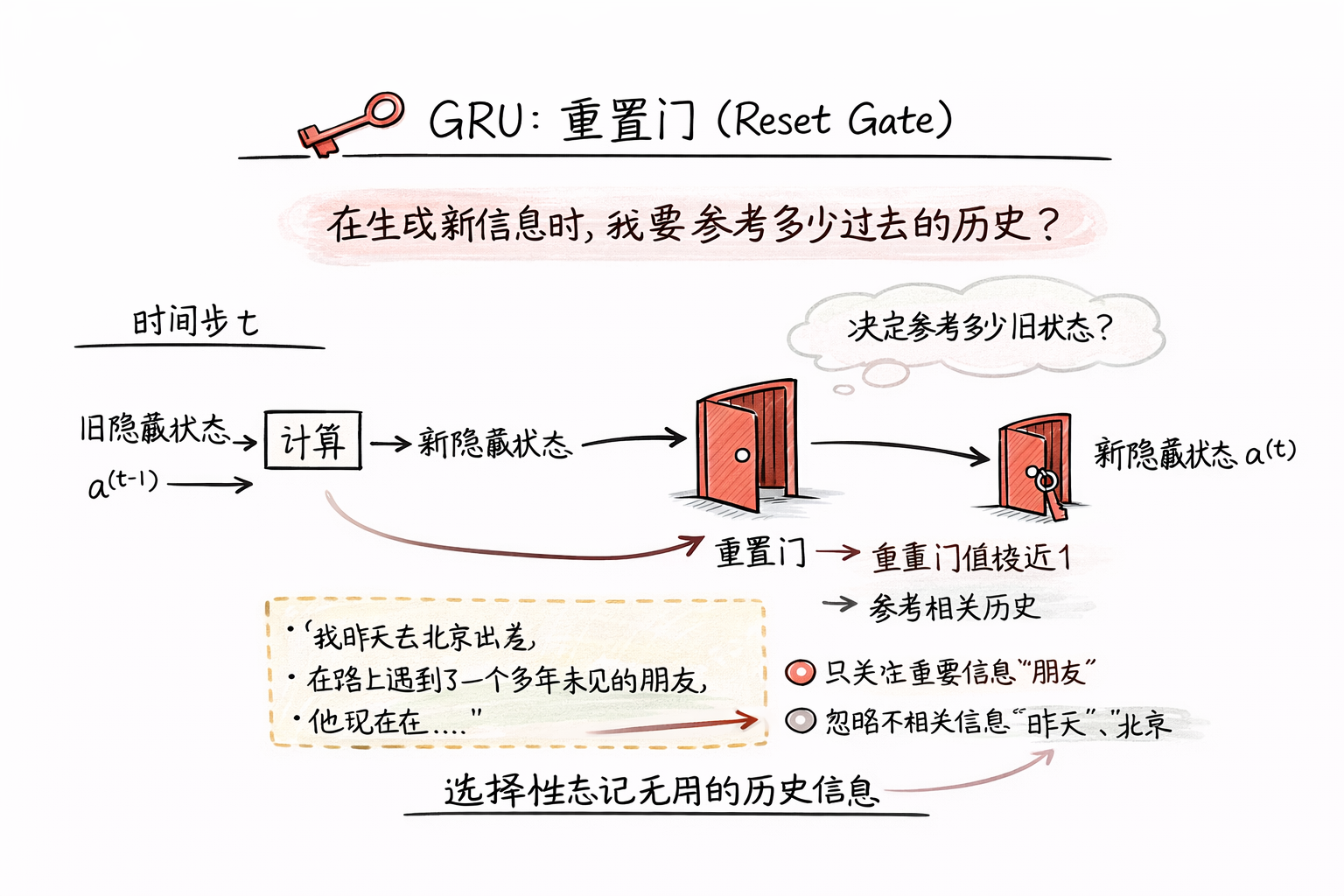
“在生成新信息時,我要參考多少過去的歷史?”
可以把它想象成 選擇記憶開關:
- 當歷史信息相關 → 重置門值接近 1 → 歷史參與計算
- 當歷史信息不相關 → 重置門值接近 0 → 模型“暫時忘掉過去”
這個設計是為了應對語言序列中的一類常見情況:句子突然換話題、上下文跳轉很大等前面的內容對當前判斷幾乎沒幫助的情況。
還是這個例子:
“我昨天去北京出差,
在路上遇到了一個多年未見的朋友,
他現在在……”
當生成“他”對應的新隱藏狀態時:
- 重置門會讓模型只關注“朋友”這個歷史信息
- 忽略“昨天”、“北京”等與當前代詞關係不大的信息
只看概念和例子, 你可能會覺得:更新門和重置門好像是一個作用啊?
實際上,這絕非冗餘設計,我們展開看看:
1.4 更新門和重置門
實際上,更新門關注的是 “舊狀態在下一步隱藏狀態中保留多少”,它是一種全局記憶控制,關注的是“以後”。
而重置門關注的是 “在生成當前新隱藏狀態時,歷史信息是否被參考”,它是一種局部選擇性,關注的是“現在”。
| 門 | 功能 | 控制對象 | 比喻 |
|---|---|---|---|
| 更新門 | 記憶持續 | 上一隱藏狀態整體傳遞 | 決定哪些歷史要帶到下一步,就像水龍頭調節水流量 |
| 重置門 | 記憶使用 | 當前候選隱藏狀態計算 | 決定本步是否參考歷史,就像選擇性翻閲筆記 |
最終,更新門負責“信息能延續多遠” ,重置門負責“信息在當前是否參與生成”。
兩道門結合,使 GRU 能夠在長序列中保留重要歷史信息,同時在必要時靈活忘掉無關歷史,實現“更好、更有用的記憶”。
現在,瞭解了 GRU 的基本原理後,我們來看看如何實現 GRU 吧。
2. 如何實現 GRU ?
這裏需要提前説明一點,如果你看了原視頻,會發現吳恩達老師並沒有過多提及重置門,而是用一個新概念:“記憶細胞” 來進行講解。實際上,記憶細胞是之後的 LSTM 中的概念,因為 GRU 可以看作是 LSTM 的簡化形式,因此同樣可以使用,但個人感覺不正式引入的前提下並不好理解,最終還是選擇使用 GRU 本身的概念來進行這部分內容,在下一篇 LSTM 的介紹中再正式引入記憶細胞。
在理解了 GRU 的核心思想和兩道門的作用之後,我們可以進一步探討如何在實際模型中實現 GRU。實現上,其實並不複雜,本質上仍是對普通 RNN 的隱藏狀態更新增加了門控計算。下面我們按邏輯逐步展開。
2.1 計算重置門
在 GRU 的實現邏輯中,對於當前步新隱藏狀態的計算,第一步是計算重置門。
重置門 \(r^{\langle t \rangle}\) 決定了歷史隱藏狀態 \(a^{\langle t-1 \rangle}\) 在生成當前候選隱藏狀態 \(\tilde{a}^{\langle t \rangle}\) 時被參考的比例。
來具體演示一下這個過程:
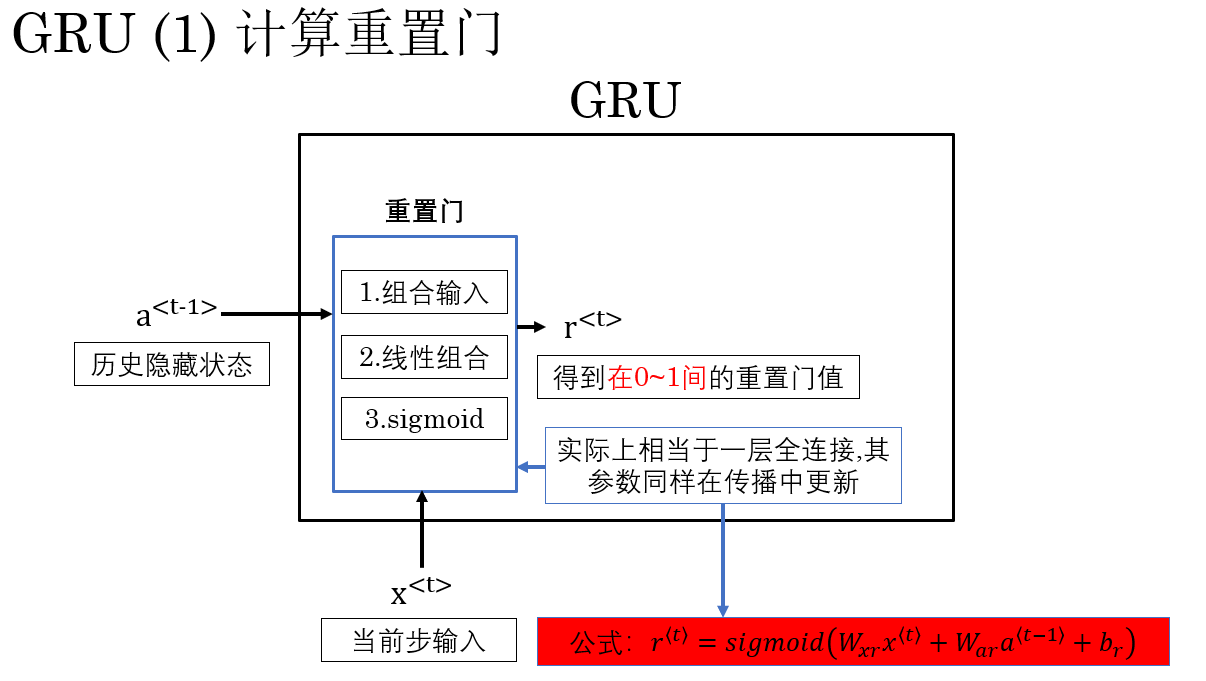
計算公式為:
你可以比較明顯的發現,實際上重置門就是一個使用 \(sigmoid\) 激活函數的全連接層,最終的激活值,也就是重置門值會被 \(sigmoid\) 壓縮到 \(0\sim1\) 之間。用來表示一種權重:
- 當 \(r^{\langle t \rangle} \approx 1\) 時,第 \(i\) 個隱藏單元會充分參考歷史信息。
- 當 \(r^{\langle t \rangle} \approx 0\) 時,第 \(i\) 個隱藏單元會 “忘掉”歷史信息,只依賴當前輸入生成候選隱藏狀態。
什麼叫候選隱藏狀態?這就是我們的下一步內容。
2.2 計算候選隱藏狀態
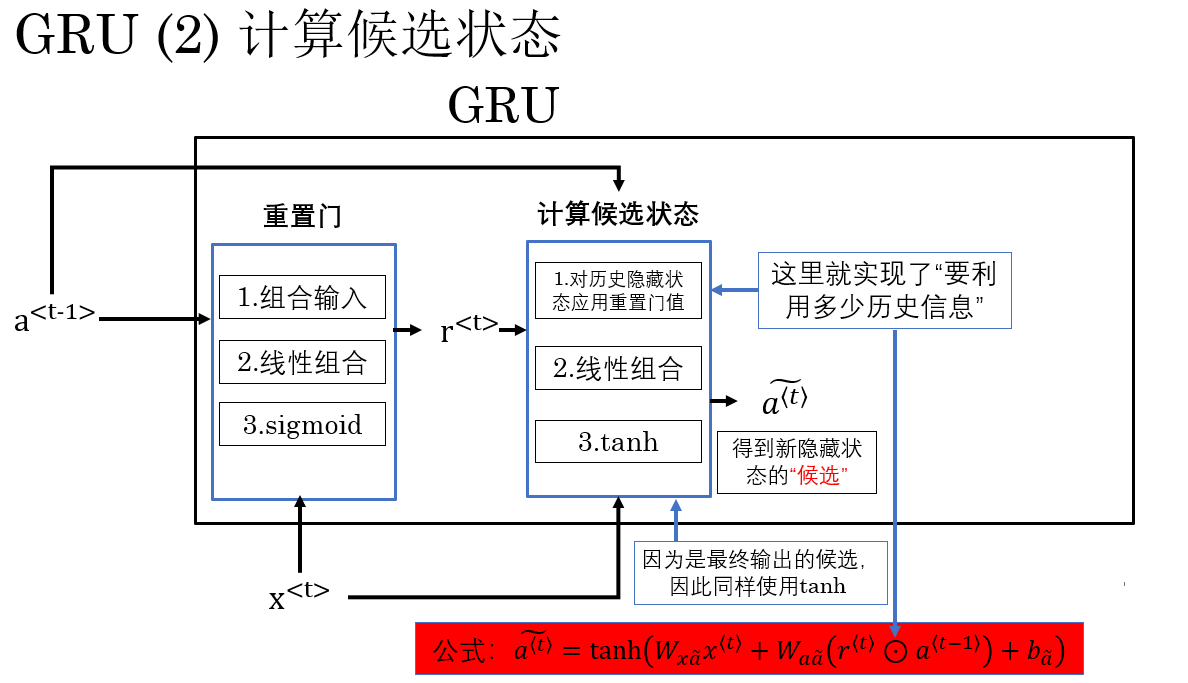
在計算完重置門 \(r^{\langle t \rangle}\) 後,下一步是生成 候選隱藏狀態 \(\tilde{a}^{\langle t \rangle}\),它表示當前步的新信息,結合了當前輸入 \(x^{\langle t \rangle}\) 和經過重置門處理後的歷史隱藏狀態 \(a^{\langle t-1 \rangle}\)。
同樣,我們在上一步的基礎上進行演示:
擺出公式如下:
其中\(r^{\langle t \rangle} \odot a^{\langle t-1 \rangle}\)是指逐元素乘,這是將重置門作用於歷史隱藏狀態。
你會發現,這時我們得到的候選隱藏狀態 \(\tilde{a}^{\langle t \rangle}\) 就是是當前步的“新記憶”,它既包含當前輸入信息 \(x^{\langle t \rangle}\),也包含經過選擇性過濾的歷史信息 \(r^{\langle t \rangle} \odot a^{\langle t-1 \rangle}\)。
到這裏,你可能覺得已經實現一些優化了,但 GRU 告訴你:這還不夠好。
2.3 計算更新門
在生成候選隱藏狀態 \(\tilde{a}^{\langle t \rangle}\) 後,下一步是計算 更新門 \(z^{\langle t \rangle}\)。
而更新門的作用是:決定歷史隱藏狀態 \(a^{\langle t-1 \rangle}\) 與候選隱藏狀態 \(\tilde{a}^{\langle t \rangle}\) 在最終隱藏狀態 \(a^{\langle t \rangle}\) 中的融合比例。
我們繼續進行演示:
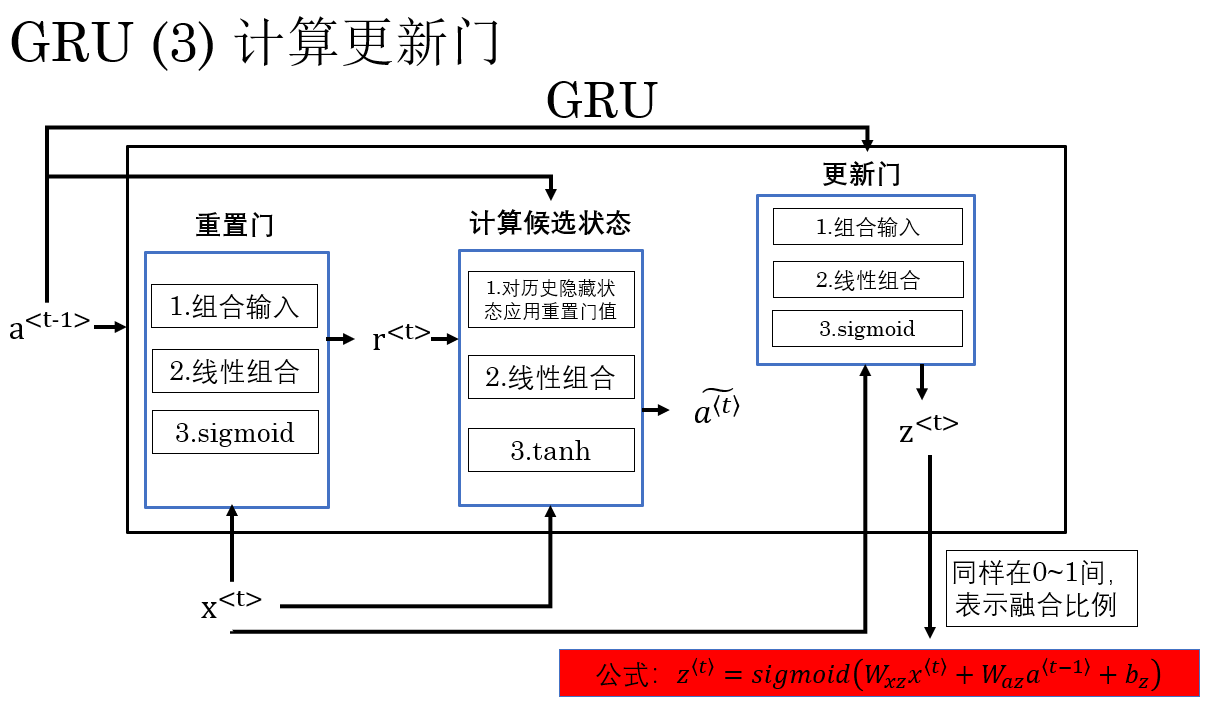
看完演示,我想一個問題已經呼之欲出了:更新門和重置門看起來就是把一個東西算了兩遍啊?這麼做的意義是什麼?我直接把重置門值拿來用不行嗎?
這就涉及到二者在模型中所承擔的語義作用:
- 更新門用來記錄全局中的重要記憶,它直接影響最終輸出,同樣梯度也直接影響它。
- 重置門用來保存局部記憶,確保使用信息符合當前步需求,它通過候選狀態間接影響最終輸出,因此梯度對它的作用就沒有那麼“長期”。
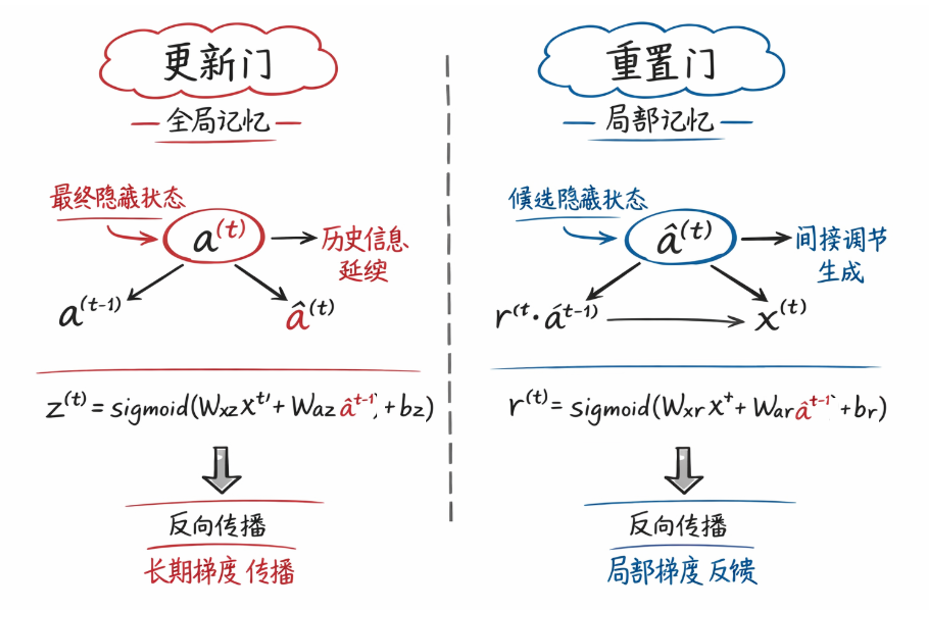
因此:二者不能參數共享,而是一定要有獨立的參數,以此通過反向傳播實現二者的語義作用。
同時要説明的是,我們這裏演示的是邏輯上的計算順序,你會發現二者的計算並不存在先後限制,因此在實際應用中可以同步計算二者。
公式表示為:
其中,\(sigmoid\) 函數將輸出壓縮到 \([0,1]\),表示融合比例:
- 當 \(z^{\langle t \rangle}_i \approx 1\) 時,第 \(i\) 個隱藏單元會更多保留歷史信息。
- 當 \(z^{\langle t \rangle}_i \approx 0\) 時,第 \(i\) 個隱藏單元會更多采納候選隱藏狀態 \(\tilde{a}^{\langle t \rangle}\) 的新信息。
最後,我們將用更新門將歷史隱藏狀態與候選隱藏狀態融合,得到最終隱藏狀態 \(a^{\langle t \rangle}\)。
2.4 計算最終隱藏狀態
在前面的步驟中,我們已經得到了三樣關鍵量:
- 上一時刻的隱藏狀態 \(a^{\langle t-1 \rangle}\)(歷史記憶)
- 當前步生成的候選隱藏狀態 \(\tilde{a}^{\langle t \rangle}\)(新記憶)
- 控制二者融合比例的更新門 \(z^{\langle t \rangle}\)
現在,GRU 要做的最後一件事,就是將“歷史記憶”和“新記憶”按更新門的指示進行融合,從而得到當前時刻的最終隱藏狀態 \(a^{\langle t \rangle}\),就像這樣:
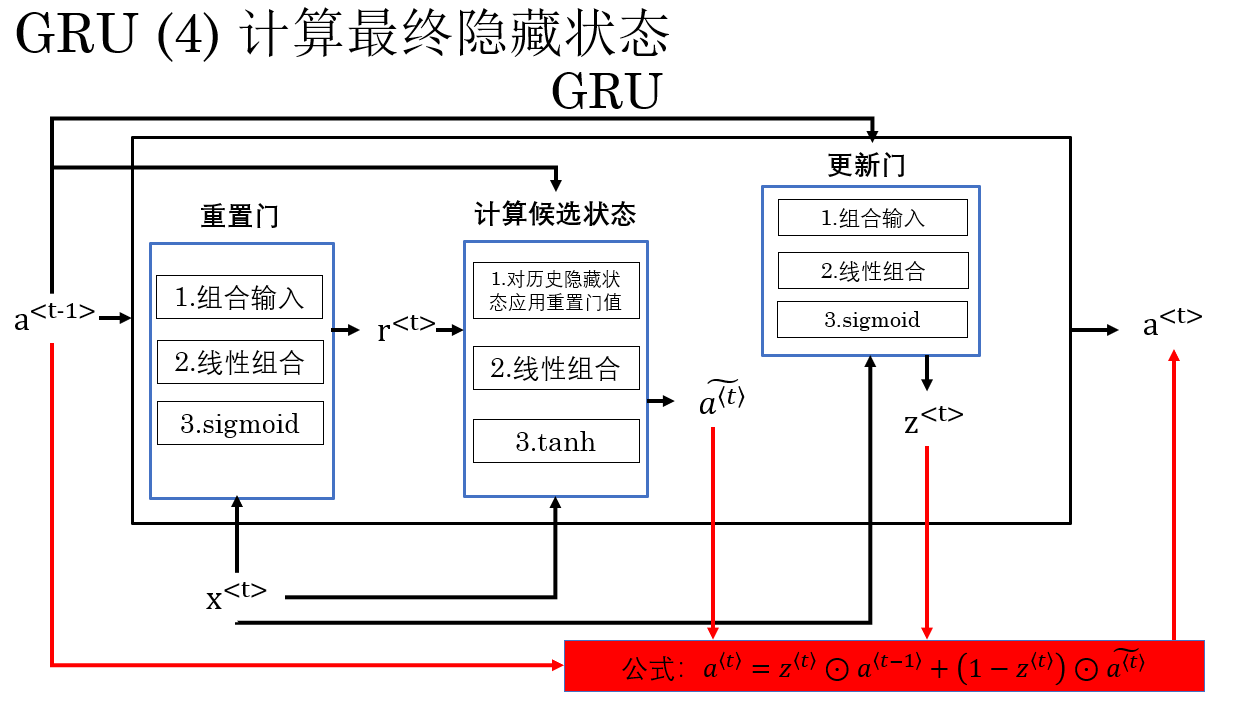
最終的計算公式為:
同樣其中 \(\odot\) 表示逐元素乘。
這個公式本身就非常直觀,它表達的正是更新門的語義含義:
- \(z^{\langle t \rangle}\) 決定了歷史信息保留的比例
- \(1 - z^{\langle t \rangle}\) 決定了新信息寫入的比例
也就是説:
- 當 \(z^{\langle t \rangle}_i \approx 1\) 時, 第 \(i\) 個隱藏單元幾乎直接複製上一時刻的狀態,信息得以長期延續。
- 當 \(z^{\langle t \rangle}_i \approx 0\) 時, 第 \(i\) 個隱藏單元主要採用當前步生成的新信息。
2.5 小結
至此,一個 GRU 單元在時間步 \(t\) 的完整計算流程就結束了,完整順序是這樣的:
- 計算重置門 \(r^{\langle t \rangle}\) → 用於調節歷史隱藏狀態在生成候選隱藏狀態 \(\tilde{a}^{\langle t \rangle}\) 時的參考程度:
- 計算候選隱藏狀態 \(\tilde{a}^{\langle t \rangle}\) → 使用當前輸入 \(x^{\langle t \rangle}\) 和重置門調節後的歷史信息 :
- 計算更新門 \(z^{\langle t \rangle}\) → 決定歷史信息與新候選狀態在最終隱藏狀態中的融合比例:
- 計算最終隱藏狀態 \(a^{\langle t \rangle}\) → 使用更新門進行加權融合:
綜合來看,GRU 緩解長距離依賴問題的方式可以概括為一句話:通過更新門建立“可複製的長期記憶通路”,通過重置門實現“按需使用的局部歷史選擇”,從結構上同時保護了信息和梯度的長期傳遞。
它並不是“記憶更強”,而是更聰明地決定什麼時候記、什麼時候用、什麼時候不動。
而且,你會發現 RGU 中同樣有殘差的思想:
從結構視角看,GRU 的更新門在時間維度上實現了一種“可學習的殘差連接”:當更新門接近 1 時,隱藏狀態幾乎被原樣複製,使信息與梯度能夠跨越多個時間步穩定傳播,這與 ResNet 通過恆等映射緩解深層網絡退化問題在思想上是一致的。
3. 總結
| 概念 | 原理 | 比喻 |
|---|---|---|
| GRU 的核心思想 | 不再“全部記住”,而是通過門控機制選擇性地記憶與使用歷史信息 | 記筆記時只標重點,而不是全文背誦 |
| 更新門(Update Gate) | 控制上一時刻隱藏狀態在當前隱藏狀態中保留的比例,直接決定最終輸出 | 水龍頭:決定舊記憶“流”到下一步的多少 |
| 重置門(Reset Gate) | 控制歷史信息在生成當前候選隱藏狀態時是否被參考 | 翻筆記:這一步要不要看以前的內容 |
| 候選隱藏狀態 | 在重置門調節下,由當前輸入與部分歷史信息生成的新記憶 | 當前這一步新寫下的草稿想法 |
| 最終隱藏狀態 | 使用更新門在舊隱藏狀態與候選隱藏狀態之間進行加權融合 | 在“照抄舊稿”和“採用新稿”之間做權衡 |
| 更新門 vs 重置門 | 更新門決定信息能“走多遠”,重置門決定信息“現在用不用” | 一個管未來,一個管當下 |
| 門不共享參數的原因 | 二者承擔不同語義角色,通過反向傳播分別學習“長期保留”和“局部使用”的策略 | 長期計劃和臨時決策不能用同一套標準 |
| 梯度傳播機制 | 更新門接近 1 時,隱藏狀態近似複製,梯度可跨時間步穩定傳播 | 給梯度修了一條高速公路 |
| GRU 與殘差思想 | 在時間維度上引入“可學習的恆等映射”,避免每一步都強制更新 | ResNet 的 skip connection,沿時間軸展開 |