1. 計算機的定義
參考現在流行的電腦,可以把計算機的設備分類為:
- 輸入:通過鍵盤、鼠標、攝像頭、網絡等方式接收數據。
- 存儲:把數據和程序保存下來(內存、硬盤等)。
- 處理:由中央處理器(CPU)、圖形處理器(GPU)、專用處理單元(如 NPU)執行運算。
- 輸出:顯示結果,或者把結果傳遞到其他設備(顯示器、打印機、網絡)。
計算機(Computer)最核心的定義是:
一種能夠自動接收、存儲、處理和輸出數據的電子設備。
2. 從計算到計算機
計算的本質是對信息做某種確定性變換。
因此可以用函數來表示:
$$y=f(x)$$
- \( x \):輸入
- \( f(·) \):函數
- \( y \):輸出
接下來嘗試將抽象計算(函數)形式化為機械模型。
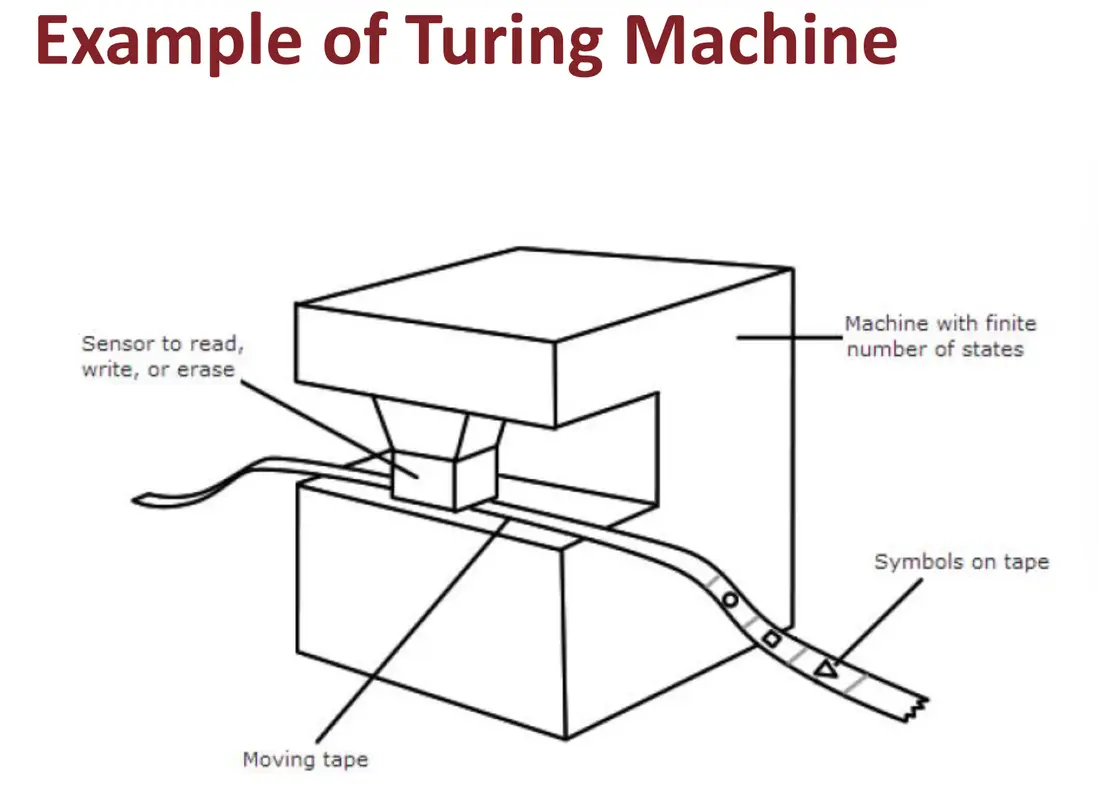
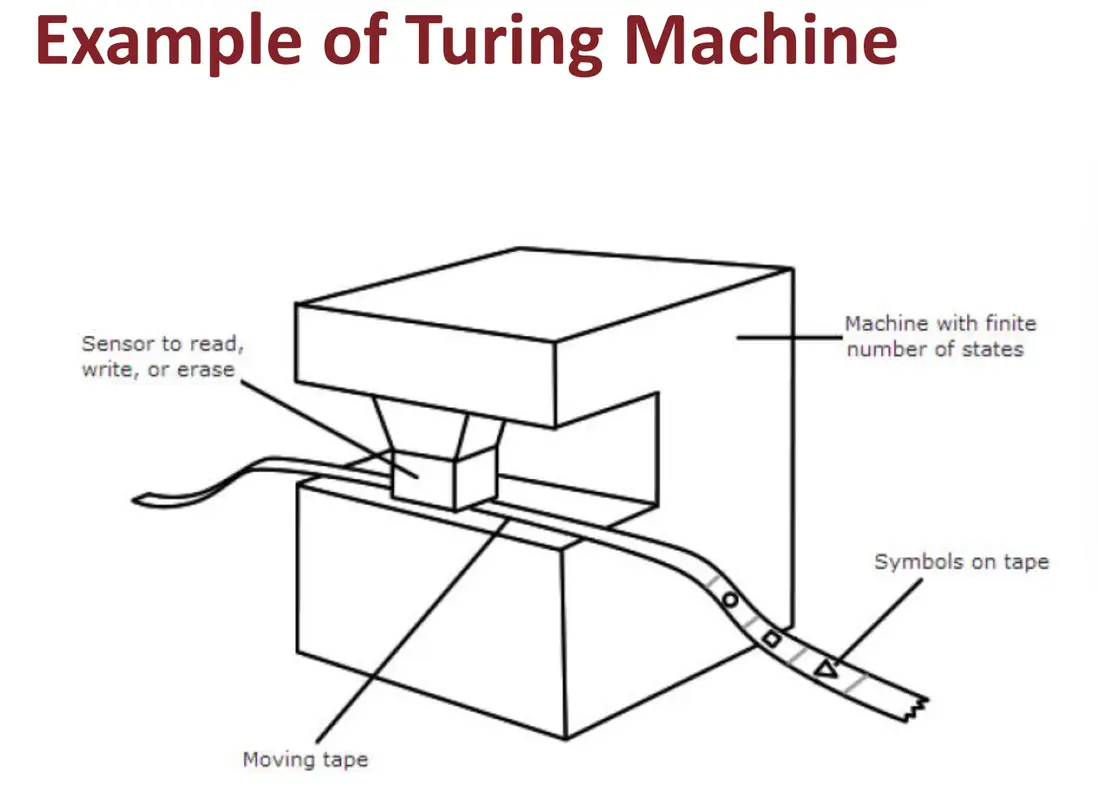
組成:
- 狀態系統(Q):控制計算步驟
- 存儲系統(紙帶):保存輸入、計算中間結果和輸出
- 轉換規則(δ): 確定下一步動作
在這種機械模型下,函數變成了:
$$處理後的紙帶=處理(處理前的紙帶)$$
在狀態系統的控制下,一步一步修改紙帶,實現複雜的函數;存儲系統在計算前保存了輸出,在計算過程中保存了中間結果,在計算後保存了輸出。
如果用數學語言來表示,即可得到圖靈機的定義:
$$ M = (Q, \Sigma, \Gamma, \delta, q_0, q_{accept}, q_{reject})$$
其中:
- \(Q\):有限的狀態集合
- \(\Sigma\):輸入字母表(不包含空白符號 \(\sqcup\))
- \(\Gamma\):紙帶字母表,滿足 \(\Sigma \subseteq \Gamma\) 且 \(\sqcup \in \Gamma\)
-
\(\delta: Q \times \Gamma \to Q \times \Gamma \times {L, R}\):轉移函數
- 輸入:當前狀態和紙帶符號
- 輸出:下一個狀態、要寫的符號、移動方向(左 \(L\) 或右 \(R\))
- \(q_0 \in Q\):初始狀態
- \(q_{accept} \in Q\):接受狀態
- \(q_{reject} \in Q\):拒絕狀態,且 \(q_{reject} \neq q_{accept}\)
計算機現實了世界中執行圖靈機等價的計算。在現實世界中,需要實現的是:
馮·諾依曼架構是圖靈機的一種簡單而直接的實現。
- 使用存儲器模仿紙帶,存放程序指令和數據。雖然在物理結構上沒有將指令和數據區分,但是在邏輯層面上指令和數據可以分別存儲到不同的存儲區域。
- 使用中央處理單元模仿狀態系統,主要負責運算和控制。
- 使用輸入輸出設備,將紙帶與外部世界相連,實現交互。比如,把圖片顯示在屏幕上。
- 使用一條系統總線,實現各種信號的傳遞,將存儲器、中央處理單元以及輸入輸出設備聯繫起來。
因此,運行流程為:
- 取指(Fetch):從存儲器讀取下一條指令
- 解碼(Decode):控制單元解析指令
- 執行(Execute):在中央處理單元中,進行運算或訪存操作
- 寫回(Write Back):將結果寫回存儲器
- 重複上述步驟,直到程序結束
將指令和數據都存放在同一存儲區、通過同一總線訪問,雖然靈活,但存在訪問衝突、速度受限的問題。Harvard架構因此應運而生,它自然地將存儲器分為指令存儲器(Program Memory)和數據存儲器(Data Memory):前者用於存儲程序指令,後者用於存儲計算所需的數據。指令和數據各自擁有獨立的總線(包括數據線、地址線和控制線),可以同時訪問,從而顯著提高執行速度。
| 架構 | 優點 | 缺點 |
|---|---|---|
| 馮·諾依曼 | 靈活、硬件簡單、程序可自修改 | 馮·諾依曼瓶頸(指令和數據共享總線) |
| Harvard | 高速、避免取指和訪存衝突 | 硬件複雜、程序修改受限 |
| 架構 | 應用場景 |
|---|---|
| 馮·諾依曼 | PC、服務器、通用 CPU、操作系統運行環境 |
| Harvard | MCU(微控制器)、DSP(數字信號處理器)、GPU 內部執行單元 |
3. 計算機角度的算法
算法作為一種複雜操作,本質上是一個可執行的步驟序列,用來解決特定問題。然而,計算機無法一次性執行這種複雜操作,因為其物理能力有限——每次只能進行簡單的算術、邏輯或存儲訪問操作。因此,各種複雜操作都是由大量簡單操作按特定順序執行實現的。
將複雜操作拆解成簡單操作會產生兩類代價:
- 時間代價:執行這些簡單操作的序列決定了計算機運行所需的時間。
- 空間代價:簡單操作的中間產物需要存儲,從而帶來存儲空間消耗。
這兩類代價直接反映了算法的效率與資源消耗,因此成為評估算法性能的兩個核心指標。
時間複雜度和空間複雜度在一定程度上是可以權衡的:面對同一個排序任務,不同的算法思路會在時間代價與空間代價之間做出取捨。比如,歸併排序通過引入大量中間變量來降低比較與移動的步驟,從而提升執行效率;而選擇排序則儘量複用原有存儲空間,以減少額外的內存開銷。