ArrayDeque（JDK雙端隊列）源碼深度剖析詳情 - 算法,集合,隊列,數據結構和算法一無是處的研究僧動態日志

ArrayDeque（JDK雙端隊列）源碼深度剖析

前言

在本篇文章當中主要跟大家介紹JDK給我們提供的一種用數組實現的雙端隊列，在之前的文章LinkedList源碼剖析當中我們已經介紹了一種雙端隊列，不過與ArrayDeque不同的是，LinkedList的雙端隊列使用雙向鏈表實現的。

雙端隊列整體分析

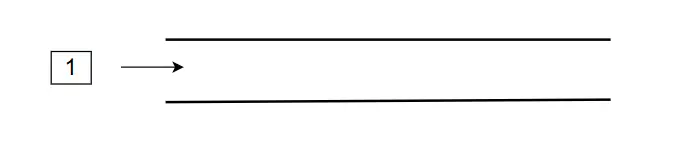
我們通常所談論到的隊列都是一端進一端出，而雙端隊列的兩端則都是可進可出。下面是雙端隊列的幾個操作：

數據從雙端隊列左側進入。
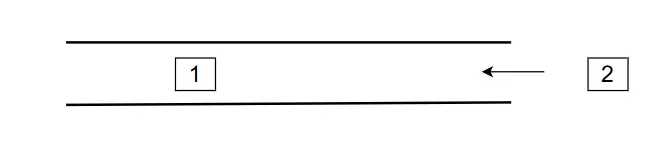
數據從雙端隊列右側進入。

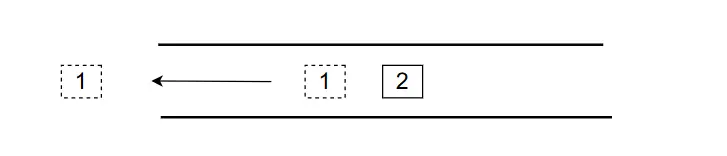
數據從雙端隊列左側彈出。

數據從雙端隊列右側彈出。

而在ArrayDeque當中也給我們提供了對應的方法去實現，比如下面這個例子就是上圖對應的代碼操作：

public void test() {
    ArrayDeque<Integer> deque = new ArrayDeque<>();
    deque.addLast(100);
    System.out.println(deque);
    deque.addFirst(55);
    System.out.println(deque);
    deque.addLast(-55);
    System.out.println(deque);
    deque.removeFirst();
    System.out.println(deque);
    deque.removeLast();
    System.out.println(deque);
}
// 輸出結果
[100]
[55, 100]
[55, 100, -55]
[100, -55]
[100]

數組實現ArrayDeque(雙端隊列)的原理

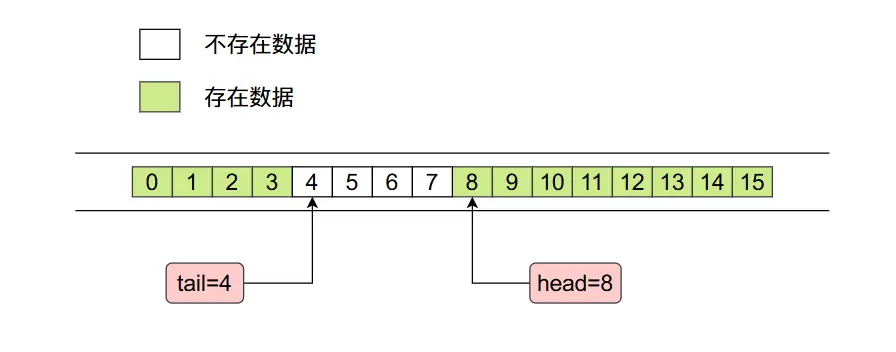
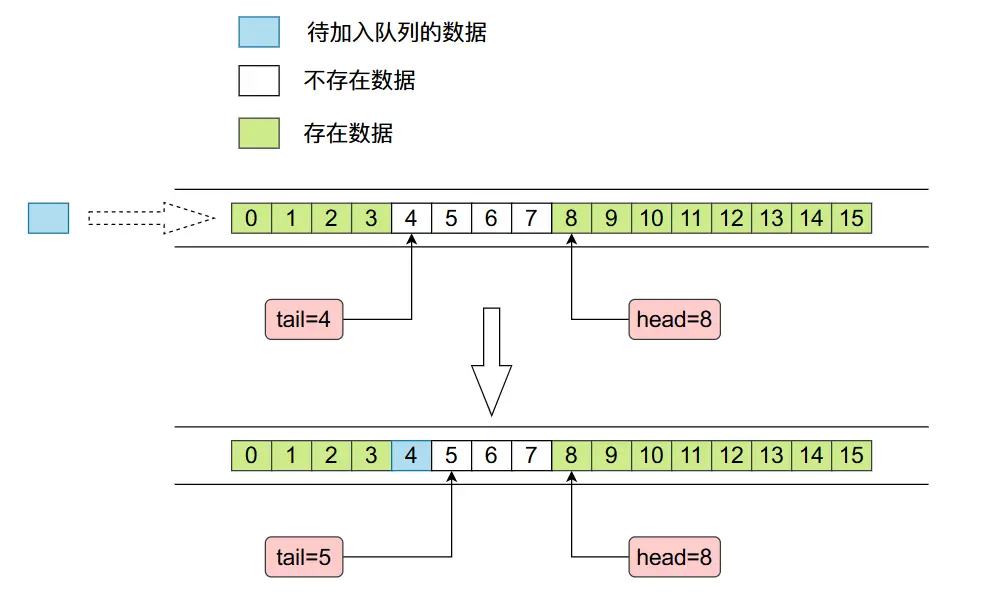
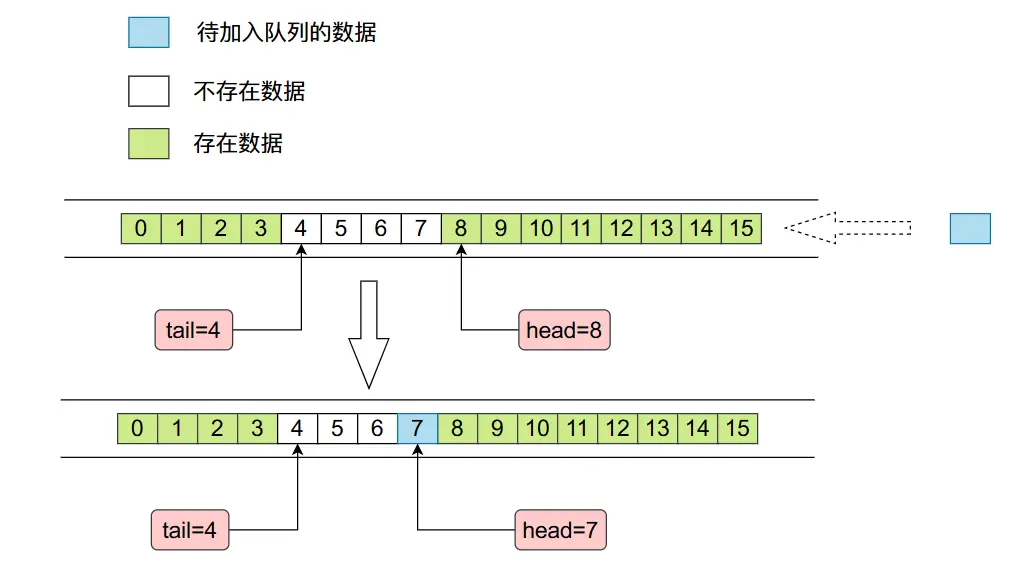
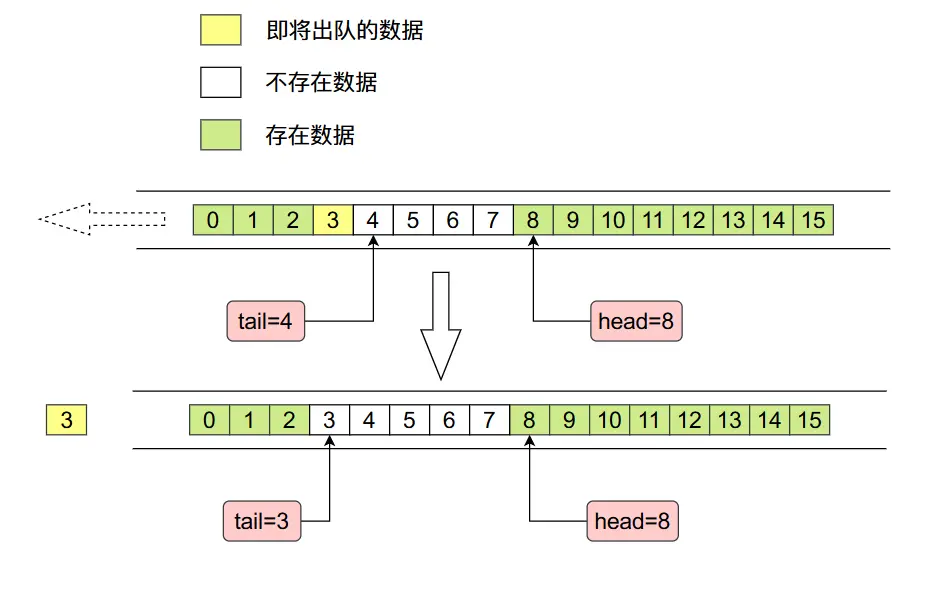
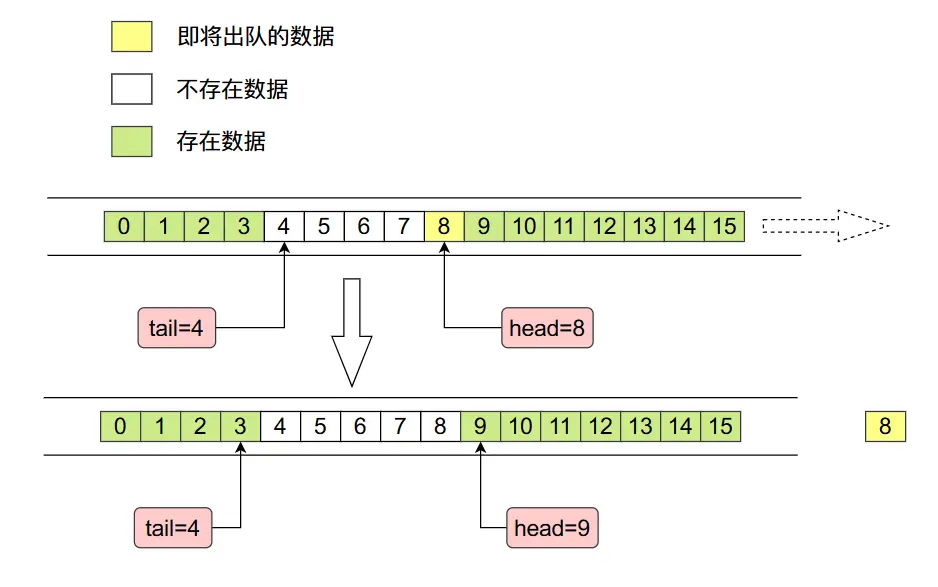
ArrayDeque底層是使用數組實現的，而且數組的長度必須是2的整數次冪，這麼操作的原因是為了後面位運算好操作。在ArrayDeque當中有兩個整形變量head和tail，分別指向右側的第一個進入隊列的數據和左側第一個進行隊列的數據，整個內存佈局如下圖所示：

其中tail指的位置沒有數據，head指的位置存在數據。

當我們需要從左往右增加數據時（入隊），內存當中數據變化情況如下：

當我們需要從右往做左增加數據時（入隊），內存當中數據變化情況如下：

當我們需要從右往左刪除數據時（出隊），內存當中數據變化情況如下：

當我們需要從左往右刪除數據時（出隊），內存當中數據變化情況如下：

底層數據遍歷順序和邏輯順序

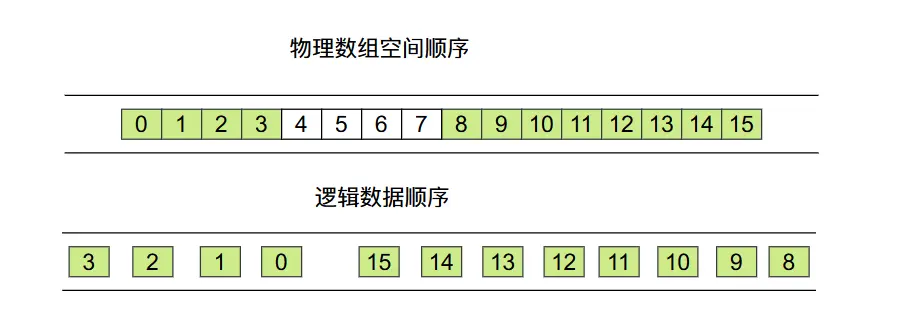
上面主要談論到的數組在內存當中的佈局，但是他是具體的物理存儲數據的順序，這個順序和我們的邏輯上的順序是不一樣的，根據上面的插入順序，我們可以畫出下面的圖，大家可以仔細分析一下這個圖的順序問題。

上圖當中隊列左側的如隊順序是0, 1, 2, 3，右側入隊的順序為15, 14, 13, 12, 11, 10, 9, 8，因此在邏輯上我們的隊列當中的數據佈局如下圖所示：

根據前面一小節談到的輸入在入隊的時候數組當中數據的變化我們可以知道，數據在數組當中的佈局為：

ArrayDeque類關鍵字段分析

// 底層用於存儲具體數據的數組
transient Object[] elements;
// 這就是前面談到的 head
transient int head;
// 與上文談到的 tail 含義一樣
transient int tail;
// MIN_INITIAL_CAPACITY 表示數組 elements 的最短長度
private static final int MIN_INITIAL_CAPACITY = 8;

以上就是ArrayDeque當中的最主要的字段，其含義還是比較容易理解的！

ArrayDeque構造函數分析

默認構造函數，數組默認申請的長度為16。

public ArrayDeque() {
    elements = new Object[16];
}

指定數組長度的初始化長度，下面列出了改構造函數涉及的所有函數。

public ArrayDeque(int numElements) {
    allocateElements(numElements);
}

private void allocateElements(int numElements) {
    elements = new Object[calculateSize(numElements)];
}
private static int calculateSize(int numElements) {
    int initialCapacity = MIN_INITIAL_CAPACITY;
    // Find the best power of two to hold elements.
    // Tests "<=" because arrays aren't kept full.
    if (numElements >= initialCapacity) {
        initialCapacity = numElements;
        initialCapacity |= (initialCapacity >>>  1);
        initialCapacity |= (initialCapacity >>>  2);
        initialCapacity |= (initialCapacity >>>  4);
        initialCapacity |= (initialCapacity >>>  8);
        initialCapacity |= (initialCapacity >>> 16);
        initialCapacity++;

        if (initialCapacity < 0)   // Too many elements, must back off
            initialCapacity >>>= 1;// Good luck allocating 2 ^ 30 elements
    }
    return initialCapacity;
}

上面的最難理解的就是函數calculateSize了，他的主要作用是如果用户輸入的長度小於MIN_INITIAL_CAPACITY時，返回MIN_INITIAL_CAPACITY。否則返回比initialCapacity大的第一個是2的整數冪的整數，比如説如果輸入的是9返回的16，輸入4返回8。

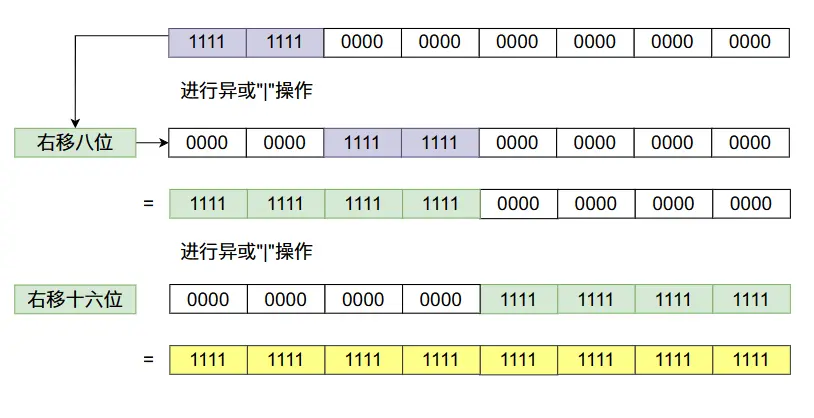
calculateSize的代碼還是很難理解的，讓我們一點一點的來分析。首先我們使用一個2的整數次冪的數進行上面移位操作的操作！

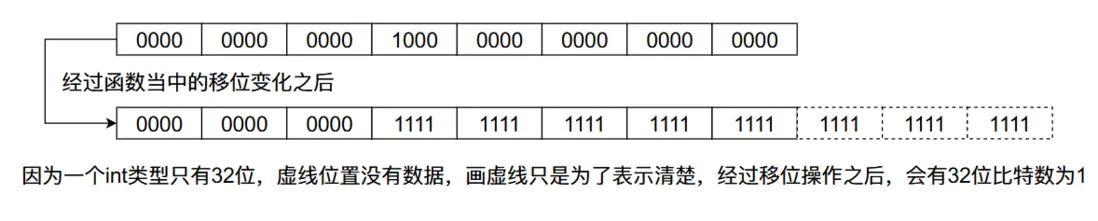
從上圖當中我們會發現，我們在一個數的二進制數的32位放一個1，經過移位之後最終32位的比特數字全部變成了1。根據上面數字變化的規律我們可以發現，任何一個比特經過上面移位的變化，這個比特後面的31個比特位都會變成1，像下圖那樣：

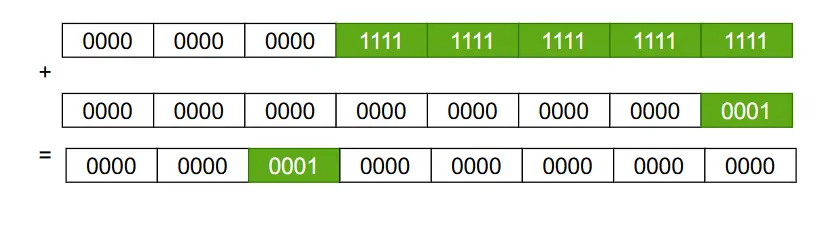
因此上述的移位操作的結果只取決於最高一位的比特值為1，移位操作後它後面的所有比特位的值全為1，而在上面函數的最後，我們返回的結果就是上面移位之後的結果 +1。又因為移位之後最高位的1到最低位的1之間的比特值全為1，當我們+1之後他會不斷的進位，最終只有一個比特位置是1，因此它是2的整數倍。

經過上述過程分析，我們就可以立即函數calculateSize了。

ArrayDeque關鍵函數分析

addLast函數分析

// tail 的初始值為 0 
public void addLast(E e) {
    if (e == null)
        throw new NullPointerException();
    elements[tail] = e;
    // 這裏進行的 & 位運算 相當於取餘數操作
    // (tail + 1) & (elements.length - 1) == (tail + 1) % elements.length
    // 這個操作主要是用於判斷數組是否滿了，如果滿了則需要擴容
    // 同時這個操作將 tail + 1，即 tail = tail + 1
    if ( (tail = (tail + 1) & (elements.length - 1)) == head)
        doubleCapacity();
}

代碼(tail + 1) & (elements.length - 1) == (tail + 1) % elements.length成立的原因是任意一個數$a$對$2^n$進行取餘數操作和$a$跟$2^n - 1$進行&運算的結果相等，即：

$$ a\% 2^n = a \& (2^n - 1) $$

從上面的代碼來看下標為tail的位置是沒有數據的，是一個空位置。

addFirst函數分析

// head 的初始值為 0 
public void addFirst(E e) {
    if (e == null)
        throw new NullPointerException();
    // 若此時數組長度elements.length = 16
    // 那麼下面代碼執行過後 head = 15
    // 下面代碼的操作結果和下面兩行代碼含義一致
    // elements[(head - 1 + elements.length) % elements.length] = e
    // head = (head - 1 + elements.length) % elements.length
    elements[head = (head - 1) & (elements.length - 1)] = e;
    if (head == tail)
        doubleCapacity();
}

上面代碼操作結果和上文當中我們提到的，在隊列當中從右向左加入數據一樣。從上面的代碼看，我們可以發現下標為head的位置是存在數據的。

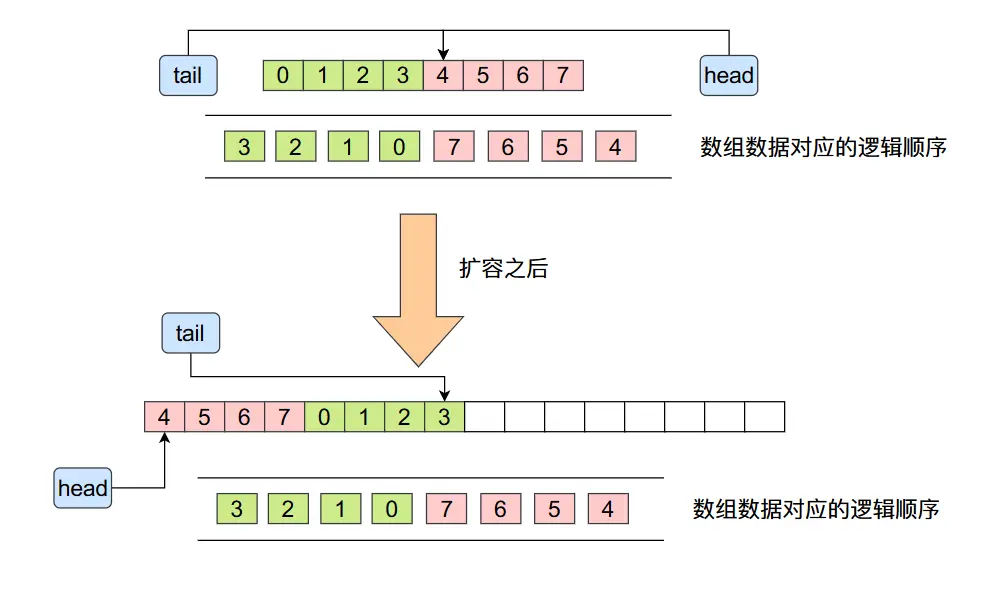
doubleCapacity函數分析

private void doubleCapacity() {
    assert head == tail;
    int p = head;
    int n = elements.length;
    int r = n - p; // number of elements to the right of p
    int newCapacity = n << 1;
    if (newCapacity < 0)
        throw new IllegalStateException("Sorry, deque too big");
    Object[] a = new Object[newCapacity];
    // arraycopy(Object src,  int  srcPos,
                                        Object dest, int destPos,
                                        int length)
    // 上面是函數 System.arraycopy 的函數參數列表
    // 大家可以參考上面理解下面的拷貝代碼
    System.arraycopy(elements, p, a, 0, r);
    System.arraycopy(elements, 0, a, r, p);
    elements = a;
    head = 0;
    tail = n;
}

上面的代碼還是比較簡單的，這裏給大家一個圖示，大家就更加容易理解了：

擴容之後將原來數組的數據拷貝到了新數組當中，雖然數據在舊數組和新數組當中的順序發生變化了，但是他們的相對順序卻沒有發生變化，他們的邏輯順序也是一樣的，這裏的邏輯可能有點繞，大家在這裏可以好好思考一下。

pollLast和pollFirst函數分析

這兩個函數的代碼就比較簡單了，大家可以根據前文所談到的內容和圖示去理解下面的代碼。

public E pollLast() {
    // 計算出待刪除的數據的下標
    int t = (tail - 1) & (elements.length - 1);
    @SuppressWarnings("unchecked")
    E result = (E) elements[t];
    if (result == null)
        return null;
    // 將需要刪除的數據的下標值設置為 null 這樣這塊內存就
    // 可以被回收了
    elements[t] = null;
    tail = t;
    return result;
}

public E pollFirst() {
    int h = head;
    @SuppressWarnings("unchecked")
    E result = (E) elements[h];
    // Element is null if deque empty
    if (result == null)
        return null;
    elements[h] = null;     // Must null out slot
    head = (h + 1) & (elements.length - 1);
    return result;
}