大家好，我是“蔣點數分”，多年以來一直從事數據分析工作。從今天開始，與大家持續分享關於數據分析的學習內容。

本文是第 4 篇，也是【數分基本功】系列的第 1 篇。該系列會講一些數據分析的基本問題，必要時增加拓展和深入。對 SQL 感興趣的同學，可以看看我的【SQL 週週練】系列（已發佈 3 篇），保證都是有挑戰性有意思的 SQL 題目。後續創作的內容，初步規劃的方向包括：

後續內容規劃

1.利用 Streamlit 實現 Hive 元數據展示、SQL 編輯器、 結合Docker 沙箱實現數據分析 Agent
2.時間序列異常識別、異動歸因算法
3.留存率擬合、預測、建模
4.學習 AB 實驗、複雜實驗設計等
5.自動化機器學習、自動化特徵工程
6.因果推斷學習

7. ……

留存率的不足

一、留存率的基本概念

1. 留存率如何定義與計算

這裏談談關於留存率的定義，如果你已經非常熟悉，可以跳過（直接要看留存率曲線的缺陷，請跳轉到第三節）

留存率曲線是用的“某一日留存”，這個“留存”是根據你想要分析的內容來定的。如果用户某一日做出了我們想要的行為，那就可以認定用户該日留存。這就是留存率的分子，而分母就是第一天滿足我們要求的用户數或設備數。

比如大家經常關心的日活躍用户 DAU，這個活躍的標準一般比較低，你打開/進入/登錄等，只要你進來了，就算上你這個用户或設備。實際執行的時候，必然牽扯到啓動接口上報（冷啓動、熱啓動、切桌面、殺後台......），也有人會結合啓動接口和幾個覆蓋面廣的埋點來統計，避免遺漏數據。

如果你關心的是某個功能或者某個業務，你還可以將統計條件設置為用户要使用 App 的某個功能或者進入某個業務的頁面，這也是一種留存。

本文談的是最常見的留存，每日新增用户 DNU 後續的留存。用户從某一天首次進入這個 App，並且被我們統計上了（設備維度或賬號維度）；留存率曲線用的是“第 x 日留存”，比如“第 7 日留存”，也就是第 7 天用户還來這個 App，才算數。否則用户就是第 3～6 天，每天都來，那也跟“第 7 日留存”無關。

2. 為什麼用“第 7 日留存”而不是“7 日內留存”

為什麼有些人更願意選擇“7 日內留存”？我一直在互聯網工作，有些部門扛着這些指標。甚至我第一次用 SQL 求留存率的時候，我也覺得——“哎，要是用户第 3～6 天來了，第 7 天沒有來，這個第 7 日留存率的指標不把人家算上，不是太可惜了。”

但如果計算留存用了“7 日內留存”，那麼“30 天”、“365 天“ 怎麼辦？比如用户第二天出現了一次，但是後面一年都不再出現了，“365 天”的留存我們也把這個用户算入。週期越長，這個指標就越虛增，這怎麼行。

#### 3. 留存率用來分析做什麼

最關鍵的，“留存率曲線”後面都跟着幾個話題：第一是 DAU 預測，DAU 就需要當天的“點”數據，來個“7 日內”這咋辦。第二就是 LT 用户生命週期，它其實就是留存曲線下面的面積/積分（説累加也行，感覺積分拽一點），同樣要求留存率是“點”計算。第三就是 LTV 用户生命週期價值：不限制天數，就是用户全生命週期價值；限制天數，就是某個時段內的用户生命週期價值。LT 都依賴於點計算，而 LTV 更是如此了。

我們本質上更關注那三個指標（DAU、LT、LTV；特別是 LTV 和 CAC 的比值，可以視為投放推廣、營銷運營活動的 ROI），這就反向限制了新增用户留存率的計算邏輯。

二、留存率曲線的擬合方法

1. 到底是用指數函數還是冪函數

指數函數的表達式為 $a \cdot e^{-bx}$

冪函數的表達式為 $a \cdot x^{-b}$

這兩個函數的差異在於：衰減的速度不一樣。把留存率 retention rate 簡寫為 $R$，指數函數是 $R_e(t) = a \cdot e^{-bt}$；冪函數是 $R_p(t) = a \cdot t^{-b}$。咱不用微分也不用差分，就直接來個 $t_0$ 和 $t_0 + \Delta{t}$，代入公式除除看：

$$\frac{R_e(t_0 + \Delta{t})}{R_e(t_0)} = \frac{a \cdot e^{-b(t_0 + \Delta{t})}}{a \cdot e^{-bt_0}} = e^{-b \Delta{t} } $$

可以看出指數函數的“衰減”，即後面某一天 $t_0 + \Delta{t}$ 相對於前面某一天 $t_0$ 的比值，與 $t_0$ 的取值無關，只和日期的間隔 $\Delta{t}$ 有關。

這也就意味着。第 2 天到第 8 天流失的比例，和第 302 天到第 308 天流失的比例是一樣的。直覺上懷疑，因為後者三百多天還來了；如果不是因為老用户召回等情況，那麼這個用户感覺挺穩定的（也需要看您公司的業務類型）如果是低頻業務：C 端用户搬家、汽車保養、旅遊、買車買房，那這種流失情況有可能出現。對於中高頻的 App 應該不會如此。

再來看看冪函數：

$$ \frac{R_p(t_0 + \Delta{t})}{R_p(t_0)} = \frac{a \cdot (t_0 + \Delta{t})^{-b}}{a \cdot {t_0}^{-b}} = (1 + \frac{\Delta{t}}{t_0})^{-b}$$

可以看出冪函數的“衰減”，與日期間隔 $\Delta{t}$ 和起始的天數 $t_0$ 都有關；如果 $t_0$ 越大，這個衰減越小。越往後流失速度越慢，這個感覺好一些。

2. 用 Python 來驗證擬合效果

最核心的函數是 scipy 庫的 optimize 下面的 curve_fit；具體計算原理，感興趣的同學請自行搜索。

a.我們先定義指數函數和冪函數的 Python 函數，然後使用 curve_fit 來獲取參數，scipy 的文檔鏈接，我已經在代碼中給出。因為我手裏缺乏實際可靠的留存率數據，我們就用 “40-20-10” 來擬合，都説它 Facebook/Meta 給的留存率標準 —— 次日留存 40%，七日留存 20%，30 日留存 10%。

請注意：實際擬合留存率時，有很多細節需要考慮。包括長期擬合的情況，以及餵給模型多少天的數據，這部分細節可以見我給出的參考鏈接 2 。

import numpy as np
from scipy.optimize import curve_fit

# 定義指數函數形式留存率函數
def exponential_ret_rate_func(t, a, b):
    return a * np.exp(-b * t)

# 定義冪函數形式留存率函數
def power_ret_rate_func(t, a, b):
    return a * np.power(t, -b)

# facebook 提出那個 40-20-10 留存率
days = [2, 7, 30]
actual_ret_rate = [0.4, 0.2, 0.1]

# 不加範圍，會提示 warning；雖然不影響結果
# https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.curve_fit.html#scipy.optimize.curve_fit
exp_ret_arg, _ = curve_fit(
    exponential_ret_rate_func,
    days,
    actual_ret_rate,
    bounds=([-np.inf, 0], [np.inf, np.inf]),
)

# 冪函數參數
pow_ret_arg, _ = curve_fit(power_ret_rate_func, days, actual_ret_rate)
all_days = np.arange(2, 31)
exp_ret_rate_arr = exponential_ret_rate_func(all_days, *exp_ret_arg)
pow_ret_rate_arr = power_ret_rate_func(all_days, *pow_ret_arg)

b.採用 RMSE 來對比一下，擬合的結果與我們給出的三個留存率的差異：

# 求求擬合的函數，與之前給出的 40-20-10 留存率差異
# 取 RMSE，np.array(days) - 2 注意起始點的序號映射關係
rmse_exponential = np.sqrt(np.mean((exp_ret_rate_arr[np.array(days) - 2] - actual_ret_rate) ** 2))
rmse_power = np.sqrt(np.mean((pow_ret_rate_arr[np.array(days) - 2] - actual_ret_rate) ** 2))

print(f"指數函數擬合的 RMSE：{rmse_exponential:.4f}")
print(f"冪函數擬合的 RMSE：{rmse_power:.4f}")

輸出的結果為：
指數函數擬合的 RMSE：0.0477
冪函數擬合的 RMSE：0.0043
（冪函數比指數函數好一個量級）

c.用 pyvchart 將兩條留存率曲線繪製出來，它是字節跳動開源的 vchart 的 Python 包。你也可以使用 pyecharts 來繪製，我一般更喜歡這種動態圖表

from pyvchart import render_chart

retent_data = [
    {"days": int(d), "retent_rate": float(round(r, 4)), "retent_func_type": "指數函數"}
    for d, r in zip(all_days, exp_ret_rate_arr)
]

retent_data.extend([
        {  "days": int(d),
            "retent_rate": float(round(r, 4)),
            "retent_func_type": "冪函數",
        }
        for d, r in zip(all_days, pow_ret_rate_arr)
])

spec = {
    "type": "line",
    "data": [{"id": "lineData", "values": retent_data}],
    "xField": "days",
    "yField": "retent_rate",
    "seriesField": "retent_func_type",
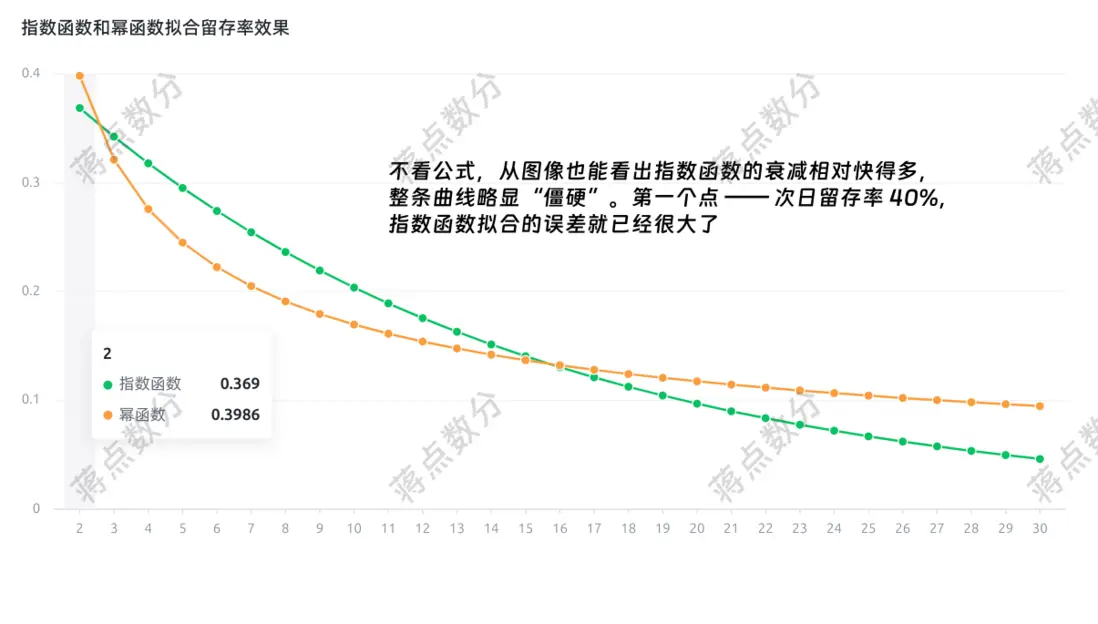
    "title": {"visible": True, "text": "指數函數和冪函數擬合留存率效果"},
}

# 在 jupyter 環境，使用 display 顯示
display(render_chart(spec))

看一下擬合的曲線，的確是冪函數形式更加適合。後續我們採用冪函數

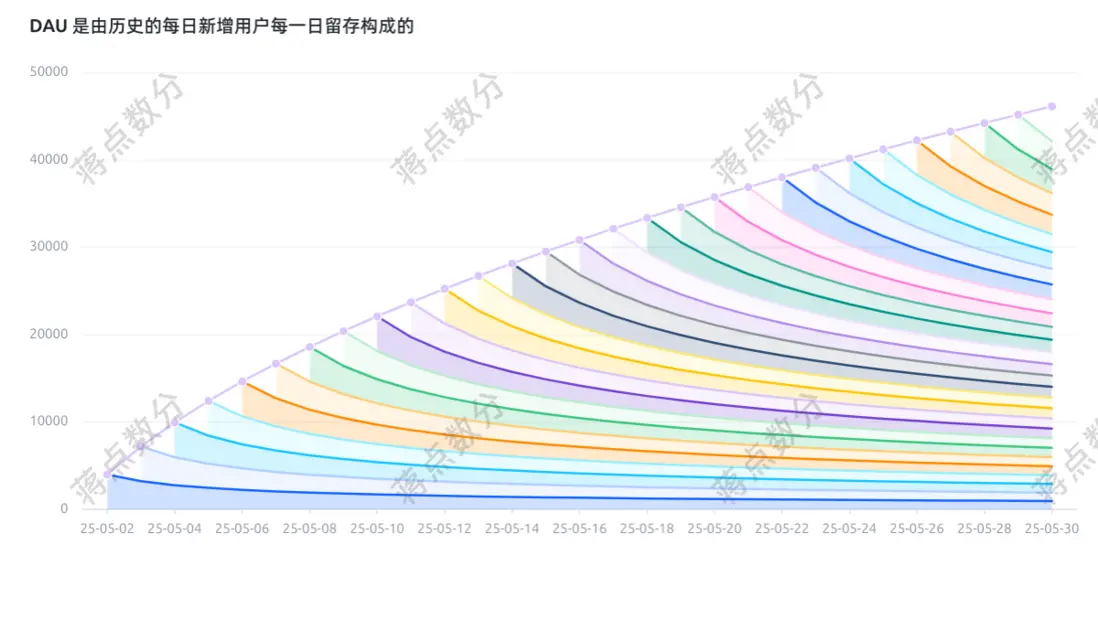
d.我們來繪製出一張特別經典的圖，每日的 DAU 其實是由歷史上每一天的新增用户的每日留存構成的。這裏為了代碼模擬簡化，假定從 2025-05-01 開始每天的新增用户都是 10000，留存率曲線每一天都用上面擬合的冪函數留存率。

pow_ret_people_num = np.round(10000 * pow_ret_rate_arr)
import datetime
start_date = datetime.date(2025, 5, 1)

all_days_formatted = [start_date+datetime.timedelta(days=int(d)-1) for d in all_days]
dau_detail = []
dau_list = []

for idx, d in enumerate(all_days_formatted):
    dau = 0
    d = d.strftime('%y-%m-%d')
    for i in range(idx+1):
        dau += int(pow_ret_people_num[idx-i])
        dau_detail.append({
            'date': d,
            'group': int(all_days[i]),
            'people_num': int(pow_ret_people_num[idx-i])
        })
    
    dau_list.append({'date': d, 'dau_num': dau})

spec = {
    "type": "line",
    "data": [{"id": "dau_detail_data", "values": dau_detail},
            {"id": "dau_data", "values": dau_list}],
    "series": [
        {
        "type": "area",
        "dataId": "dau_detail_data",
        "xField": "date",
        "yField": "people_num",
        "seriesField": "group",
        "stack": True,
        "point": {"visible": False},
        },
        {
         "type": "line",   
         "dataId": "dau_data",
         "xField": "date",
         "yField": "dau_num",
        }
    ],
    "title": {"visible": True, "text": "DAU 是由歷史的每日新增用户每一日留存構成的"},
}

# 在 jupyter 環境，使用 display 顯示
display(render_chart(spec))

可能很多同學覺得這圖太亂了，但是我想這幅圖表達的意思還是很清楚的。而且這幅圖有實際意義的，比如分析時，可以把新老用户拆開。針對老用户，不一定按照新增日期；完全可以根據其他不會改變的維度值，並且把這些維度值歸為少數幾類。這樣再畫出這幅圖，用來分析老用户留存，這就是一個不錯的展示工具。

三、留存率曲線的不足

我用上面的同樣的一條冪函數留存率，繪製出兩種不一樣的用户活躍情況（用 50 個用户做可視化模擬）。
a.第一種用户活躍情況，注意數據集結果寫入剪貼板（方便我貼到 WPS 中，我使用的 Ubuntu 沒有微軟 Office）。要分開運行，後面代碼也有寫入剪貼板

import pandas as pd
user_retention_num = np.round(50*exp_ret_rate_arr,0)

first_user_retention_user_tag = np.zeros((29,50))

for i, num in enumerate(user_retention_num):
    first_user_retention_user_tag[i][:int(num)] = 1

# to_clioboard 函數是寫入剪貼板，注意要分開運行
# 後續的寫入剪貼板會覆蓋這部分
pd.DataFrame(first_user_retention_user_tag.T).to_clipboard(index=False, header=False)

第一種活躍情況，看上去是非常極端。

b.第二種用户活躍情況

np.random.seed(2025)

second_user_retention_user_tag = np.zeros((29,50))

for i, num in enumerate(user_retention_num):
    idx = np.random.choice(50, size=int(num), replace=False)
    second_user_retention_user_tag[i][idx] = 1

df = pd.DataFrame(second_user_retention_user_tag.T)
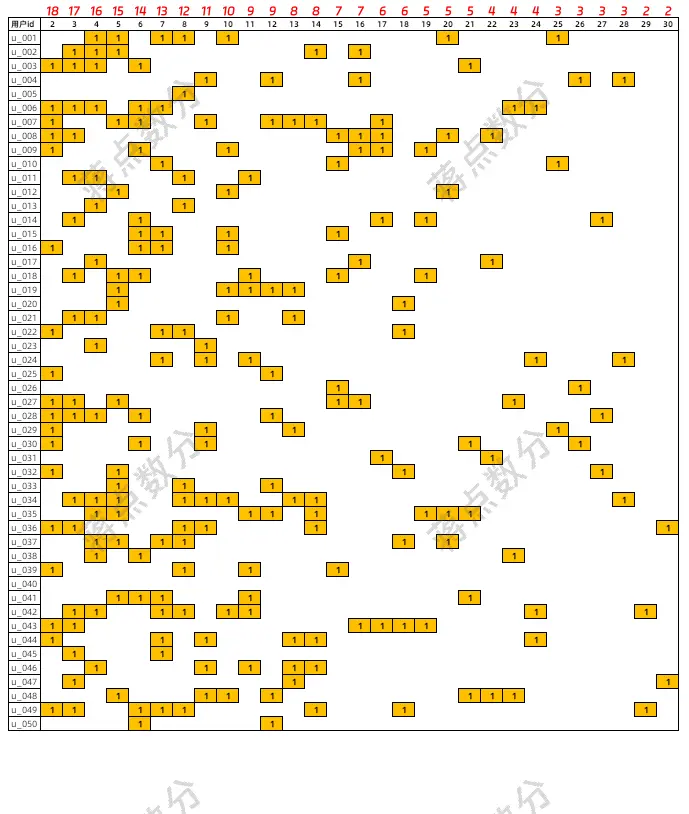
df.to_clipboard(index=False, header=False)

參考這兩張圖，大家應該都能看出來問題。可能有人覺得第二張圖有點亂，是我故意混淆大家的視覺吧。那麼我借鑑 RFM 的思路，根據用户最後一次活躍距今多少天以及總活躍天數來排序。

c.實現根據用户最後一次活躍距今多少天以及總活躍天數來排序的邏輯：

df_sort = pd.DataFrame()

df_sort['last_retent'] = df.apply(lambda row: row[row==1].index[-1] if any(row) else -1, axis=1)
df_sort['retent_days'] = df.apply(lambda row: sum(row), axis=1)

sort_order = df_sort.sort_values(by=['last_retent', 'retent_days'], ascending=[False, False]).index

df.loc[sort_order,:].to_clipboard(index=False, header=False)

此處再對比，應該明顯多了。如果我們把最後一次活躍。當成一種“包絡線”來看，後者的情況要比第一種極端情況好得多。但是兩者的留存率曲線是一樣。圖片表格最上面的紅色數字，就是公式，對錶格里整列的 1 求和；可以佐證每日留存用户數是一樣的。

也就是説留存率一致其實只能説明每日新增的用户後續“活躍的人*天”是一致的，用户的活躍分佈，甚至是真正留下的用户數量並不一致。第一種活躍情況，現實情況不會這麼極端，但是我最開始用 SQL 計算留存率時，的確隱隱感覺一種不對勁。

一般情況下，不需要什麼調整。如果需要新的指標輔助，可以增加新增用户平均活躍天數或流失用户比例等。

四、參考資料

本文關於指數函數和冪函數的啓發來自於青十五
1.青十五——《LTV預估與留存曲線擬合：指數函數還是冪函數？》

該文章提到了擬合留存率的一些細節
2.黎湘豔——《Python數據分析實戰（四）：收入、活躍預測》

😃😃😃
我現在正在求職數據類工作（主要是數據分析或數據科學）；如果您有合適的機會，即時到崗，不限城市。