在當今的數字化時代,以音視頻等多媒體內容為代表的非結構化數據呈現出爆炸式增長。這類數據無法簡單地用傳統數據庫中的行列數據來表示,因此向量檢索技術應運而生。非結構化數據通常被轉換為向量表示,並存儲在向量數據庫中。這種向量化模型能夠提取並捕捉到數據中的特徵,在多維的向量空間中進行有效表示。
一個形象的例子是:embedding(king)−embedding(man)+embedding(woman)≈embedding(queen)
13 倍的速度,背後到底藏着什麼秘密?
在最新的 OpenSearch 實踐中,我們引入 GPU 並行計算能力 與 NN-Descent 索引構建算法,成功將億級數據規模下的向量索引構建速度提升至原來的 13 倍。
在算法性能部分,GPU 上的 NN-Descent 比 32 核 CPU 快約 20 倍,結合產品集成優化後整體速度提升約 10 倍。更重要的是,GPU 構建幾乎不佔用 CPU 資源,騰出的算力還可用於其他任務,實現更高資源利用率。
在生產環境中,客户數據規模常常達到數億,經典 HNSW 算法的索引構建往往需要花費半天,甚至數天的時間來完成,用户體驗較差。
針對這一問題,我們進行了創新性的技術嘗試,把 GPU 加速的 NN-Descent 算法引入到索引構建階段,替代傳統的 HNSW 算法。這種基於 GPU 的算法能夠充分利用其大規模並行計算能力,從而顯著加快索引構建速度。
通過在億級數據集上進行測試,我們觀察到了高達 13 倍的提速。這項技術不僅有效降低了部署成本,緩解了計算資源的壓力,同時也提升了用户體驗,維護了性能與成本的理想平衡。
向量檢索算法簡介
向量檢索的核心任務是從向量索引中找出與查詢向量最相似的向量集合。為了平衡效率與精度,實際應用中通常採用 近似算法 代替精確匹配,以降低計算成本。
這些 近似算法 按 實現方式 可以主要分為以下幾類:
- 圖索引:包括 HNSW 和 DiskANN。這類算法通過構建圖結構以便數據點快速訪問和檢索。
- 量化索引:如 PQ(乘積量化)、HC(層次量化)、QC(量化聚類),以數據量化壓縮來提升效率。
- 哈希索引:如 LSH(局部敏感哈希),利用哈希函數將數據散列到不同的桶中,加快檢索速度。
其中,HNSW 是目前最為廣泛使用的算法,其索引結構與跳錶(Skip List)類似,擁有多層圖,上一層節點是下一層節點的稀疏表示。底層圖提供最詳盡的數據點,而上層圖則簡化了移動計算,允許在向量空間中快速接近目標。在向量檢索過程中,上層圖可加速初步鄰近目標的定位,而底層圖負責精細化查找,確保準確性。
在後續小節中,本文將先對 GPU 進行介紹,隨後探討如何利用其計算特性推進向量索引的構建加速方法。
GPU 基礎知識
最初,GPU 被設計用於圖形繪製,但隨着開發者逐漸認識到其在通用並行計算中的優勢,GPU 演變為深度學習和高性能計算的關鍵硬件。本節將主要圍繞廣泛使用的英偉達(Nvidia)GPU 進行討論。
相比傳統的中央處理單元(CPU),GPU 擁有數百甚至數千個核心,這些核心可以同時執行許多簡單的計算任務。這種並行計算能力允許 GPU 以極高的效率處理大量數據,比如在深度學習中的大量矩陣運算。
隨着 2017 年 Volta 架構的推出,Nvidia GPU 加入了 Tensor Core 硬件單元,該單元專門用於加速矩陣乘法計算,使得 GPU 的計算能力進一步提升。
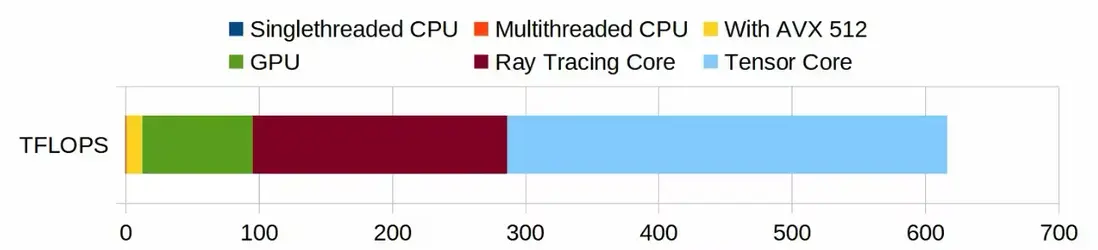
下面的圖示比較了一台家用 PC(Ryzen 9950X + 4090)中 CPU 與 GPU 的計算性能:
- 在假設 CPU 的每週期指令數(IPC)為 4 、睿頻為 5.7GHz 時,單核性能可達 22.8 GFLOPS(深藍部分,圖中幾乎不可見)。如果使用全部 32 個核心並結合 AVX512 指令(單指令處理 16 個單精度浮點數),性能指標可以達到 10 TFLOPS(黃色部分)
- 另一方面,RTX 4090 的 CUDA Core 在 FP16 精度下的計算能力達到 82 TFLOPS(綠色部分)
- RTX 4090 的 Tensor Core 在 FP8 精度下的計算能力更是高達 660 TFLOPS(淺藍部分)
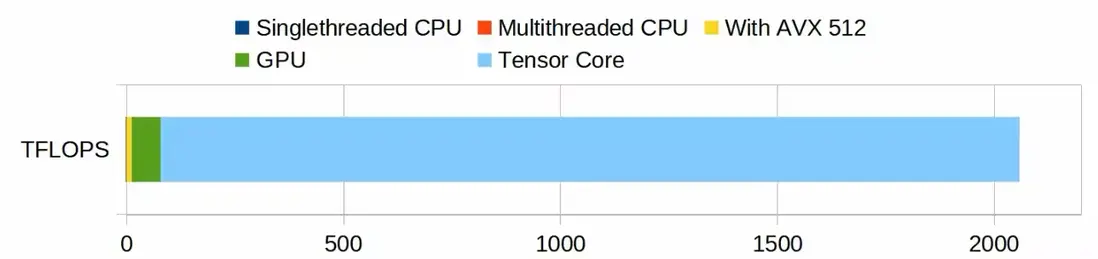
如果我們以 H100 GPU 作為比較對象,GPU的優勢將更加明顯:
如何利用其計算特性推進向量索引的構建加速方法:
雖然在現實應用中,很多任務都無法充分利用如此高的並行度或依賴矩陣運算,但幸運的是,我們發現 NN-Descent 算法能夠很好地發揮 GPU 的計算優勢。
什麼是 NN-Descent?
NN-Descent 是一種構建近鄰圖(proximity graph)的算法,簡單來説,近鄰圖中點的鄰居就是那些與其向量距離相近的點。與 HNSW 算法不同,NN-Descent 構建的圖僅有一層,這可以理解為 HNSW 中包含所有點的第 0 層,此外,NN-Descent 圖中所有點的鄰居數量都是固定的,這是出於並行計算的考慮。
NN-Descent 算法的核心思想是”我鄰居的鄰居,可能是離我更近的鄰居“,其建圖流程是一個迭代做全量更新的過程,在每輪迭代中,對每個點,都會去找它所有的二階鄰居(即鄰居的鄰居),嘗試用這個集合去優化它原本的鄰居集合(即我鄰居的鄰居,可能比我當前的鄰居離我更近),如此迭代直到收斂。以下是對其計算流程一些關鍵問題的簡化解釋。
NN-Descent 關鍵問題的解釋:
- NN-Descent 如何將向量距離計算轉化為矩陣乘問題?
以歐式距離 (a - b) ^ 2 為例,將其展開 a^2 + b^2 - 2ab,前兩項都是天然並行的,而批量計算時,用向量集合 A 與集合 B 的內積(即第三項)完全等價於矩陣乘計算,這是 NN-Descent 能在 GPU 上高效執行的理論基礎。 - NN-Descent 具體是如何在 GPU 上運算的?
實際計算時,為提高效率,算法並不會遍歷點的所有二階鄰居,而是去採樣當前點的出邊鄰居與入邊鄰居(例如 {a, b} -> cur -> {c, d}),在採樣集合({a, b, c, d})內兩兩計算距離,並嘗試更新集合內各元素的鄰居列表。
對每一輪迭代,假設數據集大小為 N,每個點的出邊與入邊採樣數為 64,則更新所需的的總計算量為 N x 64 x 64 個向量內積,每個點的計算量為 64 x 64 個向量內積。每輪更新中,每個點會佔用一個 GPU block,其 thread\_num = 512,等價於 16 個 warp(GPU 以 32 個 thread 為最小執行單位,稱為一個 warp),每個 warp 負責其中 16 x 16 個向量距離的計算。
NN-Descent 如何與 HNSW 進行對接:
NN-Descent 得到的圖只有一層,而 HNSW 一般使用多層圖去查詢,所以該如何進行對接呢?對此,我們嘗試了三種方案:
- 直接使用單層圖,選取數個查詢起點,查詢時從距離查詢結果最近的起點開始搜索;
- 走 hnsw 建圖流程構建底層以外的層;
- 走 nn-descent 建圖流程構建底層以外的層。
實測三種建圖方式在建圖速度、查詢效果上沒有明顯差距。我們最終選擇第三種方案,以便更好結合現有 HNSW 查詢框架的查詢邏輯。
OpenSearch 實踐
我們在大小兩個數據集上測試了算法的性能與效果表現,CPU 側的比較對象為 OpenSearch 向量檢索版 1.4.0 版本 的 HNSW 算法實現。
NN-Descent 核心需要調節的參數為 ‘intermediate\_graph\_degree ’與 ’graph\_degree‘,前者為 GPU 建圖時點的鄰居數,後者是經過裁邊後最終圖的鄰居數。
小數據集為 100W 960 維 的 GIST 數據集,在開發機上進行測試,耗時上僅對比核心建圖算法部分。A10 GPU 耗時 ++27s++,32 核 CPU 圖耗時 ++587s++,是 GPU 的 ++21.74 倍++。召回效果上,GPU 略弱於 CPU,但通過提升 ef,能夠達到相似的召回率上限。
| 算法(框架) | Build Params | Time Used (s) | ef when Top10 Recall is 99.5% |
|---|---|---|---|
| HNSW(hnswlib 32Core) | M = 100 ef\_construction = 500 | 619 | 500 |
| HNSW(OpenSearch 32Core) | M = 100 ef\_construction = 500 | 587 | 110 |
| NN-Descent(OpenSearch) | graph\_degree=96, intermediate\_graph\_degree=128 | 27 | 220 |
大數據集為 1.13 億 1024 維的 Cohere 數據集,在產品中進行測試(大數據集時不再對比 hnswlib 的結果):
| Build Params | Time Used | 分配的 CPU 核數 | Node Count |
|---|---|---|---|
| M = 100 ef\_construction = 500 | ~13 hours | 16 | 5 |
| graph\_degree=64, intermediate\_graph\_degree=96 | ~1 hour | 2 | 5 |
大數據集 Top100 相同召回率下的查詢性能:
查詢節點分配的資源為 ++16 核 * 10 分片++,實際環境可根據需求擴容
| Recall | 算法 | Query Param | Concurrency | QPS | Latency (ms) |
|---|---|---|---|---|---|
| 0.95 | HNSW | max\_scan\_ratio=0.001 ef=100 | 1 | 47 | 21 |
| 4 | 199 | 20 | |||
| 16 | 554 | 28 | |||
| NN-Descent | max\_scan\_ratio=0.001 ef=100 | 1 | 55 | 18 | |
| 4 | 202 | 19 | |||
| 16 | 574 | 27 | |||
| 0.98 | HNSW | max\_scan\_ratio=0.003 ef=100 | 1 | 40 | 24 |
| 4 | 152 | 26 | |||
| 16 | 413 | 38 | |||
| NN-Descent | max\_scan\_ratio=0.05 ef=130 | 1 | 31 | 32 | |
| 4 | 113 | 35 | |||
| 16 | 282 | 56 | |||
| 0.99 | HNSW | max\_scan\_ratio=0.05 ef=130 | 1 | 31 | 32 |
| 4 | 113 | 35 | |||
| 16 | 296 | 54 | |||
| NN-Descent | max\_scan\_ratio=0.05 ef=500 | 1 | 15 | 66 | |
| 4 | 55 | 71 | |||
| 16 | 132 | 120 | |||
| 0.995 | HNSW | max\_scan\_ratio=0.05 ef=300 | 1 | 17 | 57 |
| 4 | 64 | 62 | |||
| 16 | 156 | 102 | |||
| NN-Descent | max\_scan\_ratio=0.05 ef=1500 | 1 | 12 | 84 | |
| 4 | 44 | 90 | |||
| 16 | 104 | 153 |
參考文獻
1.Initial CUDA Performance Surprises
2.NN-Descent
3.GPU NN-Descent
結尾
綜合而言,基於 NN-Descent 算法的 GPU 向量索引構建在理論上比傳統 CPU 的性價比提升超過 10 倍。然而,由於前後處理與調度操作佔用了部分時間,當前產品中 GPU 的實際利用率未達預期,其實際性價比約為 5 倍。
在算法性能方面,GPU 上的 NN-Descent 比傳統 CPU 實現快約 20 倍(基於 32 核的比較),產品集成後整體速度提升約 10 倍。當然,這項技術也並非沒有缺陷:
- 同查詢參數時,GPU 建圖的召回率比 CPU 建圖低約 1 - 1.5 個百分點,但通過調節查詢參數,可以達到相同水準。
- 相較於 32 核 CPU 機型,32 核 A10 GPU 機型的成本高約一倍,然而,由於算法幾乎不佔用 CPU 資源,CPU 可以用於運行其他任務。
未來,我們計劃通過優化任務調度策略來進一步提高 GPU 的利用效率。此外,我們也將探索優化策略,嘗試在適度犧牲構建性能的情況下,進一步提升召回率以滿足更高精度需求。這些改進將有助於實現更為均衡的成本效益比,提高生產應用中的效率與效果。