一、基礎介紹
什麼是 mul 與 reduce\_sum?
mul 通常指元素級乘法(Element-wise Multiplication),它將兩個形狀相同的張量中對應位置的元素相乘,返回一個與原張量形狀相同的新張量。
reduce\_sum 是一種規約操作(Reduction Operation),它沿指定維度對張量的元素求和,從而 “壓縮” 或 “減少” 張量的維度。如果不指定維度,則對所有元素求和,返回一個標量。
二、baseline 結構
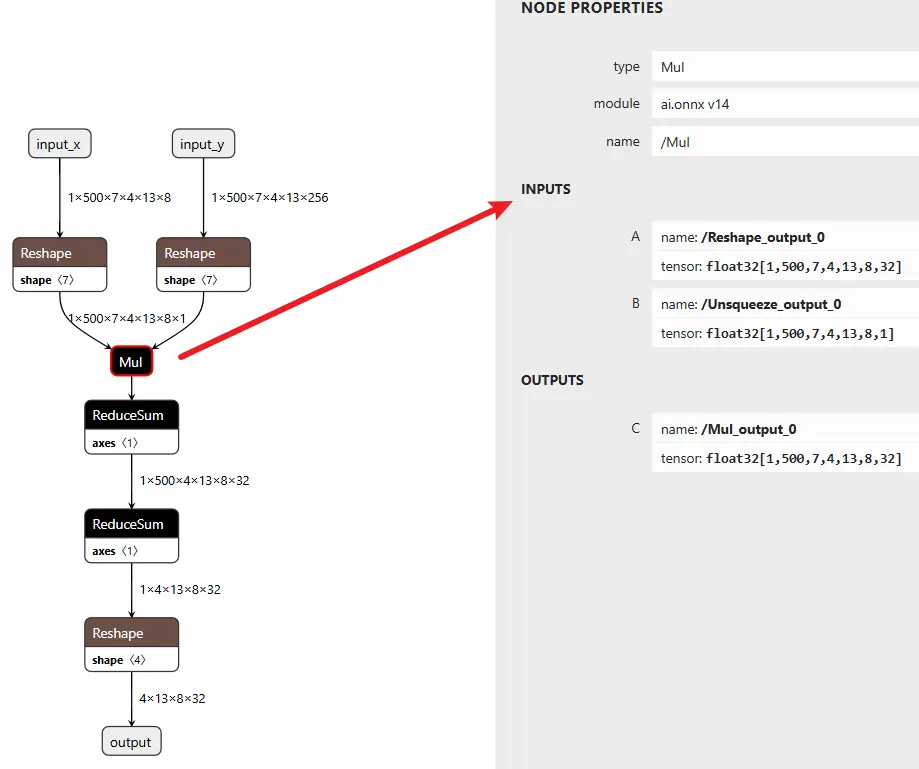
onnx 可視化圖如下:
對應代碼如下:
class CustomNet(nn.Module):
def __init__(self):
super(CustomNet, self).__init__()
def forward(self, a, b):
# a: shape (1, 500, 7, 4, 13, 8)
# b: shape (1, 500, 7, 4, 13, 256)
# Step 1: Unsqueeze a -> (1, 500, 7, 4, 13, 8, 1)
a = a.unsqueeze(-1)
# Step 2: Reshape b -> (1, 500, 7, 4, 13, 8, 32)
b = b.view(1, 500, 7, 4, 13, 8, 32)
# Step 3: Mul (broadcast over last dim)
out = a * b # shape: (1, 500, 7, 4, 13, 8, 32)
# # Step 4: ReduceSum over dim=2 (index 2 = 7 dim)
out = out.sum(dim=2) # shape: (1, 500, 4, 13, 8, 32)
# # Step 5: ReduceSum over dim=1 (500 dim)
out = out.sum(dim=1) # shape: (1, 4, 13, 8, 32)
# Step 6: Reshape to final output
out = out.view(-1, 13, 8, 32) # 可根據需要調整最終輸出 shape
return out
a = torch.randn(1, 500, 7, 4, 13, 8)
b = torch.randn(1, 500, 7, 4, 13, 256)
model = CustomNet()
output = model(a, b)在征程 6M 上進行簡單的模型編譯與性能預估:
hb_compile -m mymodel.onnx --march nash-m --fast-perf根據產出物得到預估 latency:2.97 ms
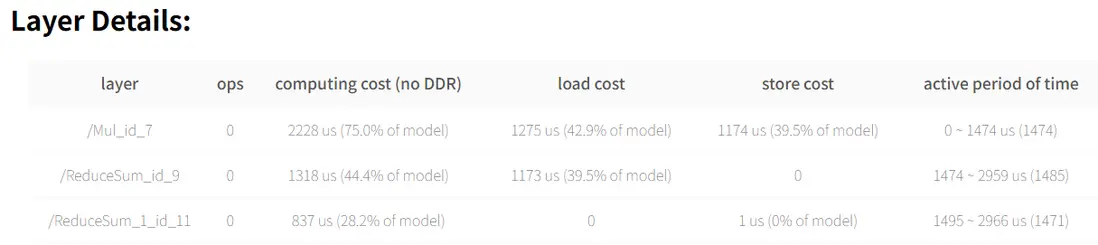
這個結構如何進行優化呢?
三、合併 reduce\_sum
# Step 4: ReduceSum over dim=2 (index 2 = 7 dim)
out = out.sum(dim=2) # shape: (1, 500, 4, 13, 8, 32)
# Step 5: ReduceSum over dim=1 (500 dim)
out = out.sum(dim=1) # shape: (1, 4, 13, 8, 32)這兩個 reducesum 能合併成一個,使用 dim=(1, 2)(即同時對 dim=1 和 dim=2 做 sum),前提是這兩個維度的求和沒有先後順序依賴(即兩個維度是獨立的)
out = out.sum(dim=(1, 2)) # 一次性對 dim=1 和 dim=2 求和PyTorch 中 。sum(dim=(1, 2)) 會按照給出的維度一次性執行 sum 操作,等價於逐個做 dim=2 然後 dim=1,因為 sum 是可交換的操作,最終結果形狀完全相同。
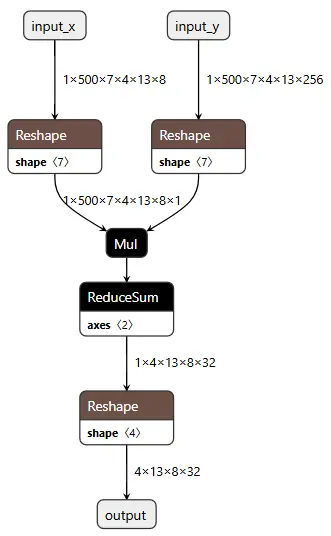
優化後結構如下,可以看到確實少了一個 reducesum:
預估 latency: 1.75 ms
四、mul+reducesum 變成 conv
假設有兩個張量:
- a.shape = (B, C, H, W)
- b.shape = (B, C, H, W)
常見操作是:
out = (a * b).sum(dim=[2, 3]) # 在 H 和 W 上求和,輸出 shape: (B, C)
# ----------細節---------------
import torch
import torch.nn as nn
a = torch.randn(1, 3, 8, 4) # 多維時,a的最後一維若與b不同,則只能是1,否則不能進行廣播
b = torch.randn(1, 3, 8, 4)
c = a * b # c的shape:torch.Size([1, 3, 8, 4])
d = c.sum(dim=[2,3]) # d的shape:torch.Size([1, 3])注意:torch 中 a * b 是逐元素相乘(mul),而不是矩陣乘法(matmul),形狀不匹配時會觸發廣播(複製對應列 or 行)
通過 深度卷積(depthwise convolution) 可以近似實現 Mul + ReduceSum 操作,等價的 Conv2d 實現方式,可以用 groups=B*C 的 conv2d 來實現上述操作:
import torch
import torch.nn.functional as F
def conv_approx_mul_reducesum(a, b):
B, C, H, W = a.shape
# 把 b 變成卷積核,作為每個通道的 filter
kernel = b.reshape(B * C, 1, H, W)
# 輸入 reshape 成 (1, B*C, H, W)
input_ = a.reshape(1, B * C, H, W)
# 深度卷積實現 mul+sum,輸出 shape: (1, B*C, 1, 1)
output = F.conv2d(input_, kernel, groups=B * C)
# reshape 回 (B, C)
return output.reshape(B, C)conv2d 的過程是:
- 對每個通道進行 乘法(卷積)
- 然後在 kernel 區域內 求和
所以 F.conv2d(a, b, groups=B*C) 本質就是:對 a 和 b 逐元素相乘再求和 = Mul + ReduceSum
一致性驗證:
import torch
import torch.nn as nn
import torch.nn.functional as F
a = torch.randn(1, 3, 8, 4) # 多維時,a的最後一維若與b不同,則只能是1,否則不能進行廣播
b = torch.randn(1, 3, 8, 4)
c = a * b # c的shape:torch.Size([1, 3, 8, 4])
d = c.sum(dim=[2,3]) # d的shape:torch.Size([1, 3])
print(d)
def F_conv2d_approx_mul_reducesum(a, b):
B, C, H, W = a.shape
# 把 b 變成卷積核,作為每個通道的 filter
kernel = b.reshape(B * C, 1, H, W)
# 輸入 reshape 成 (1, B*C, H, W)
input_ = a.reshape(1, B * C, H, W)
# 深度卷積實現 mul+sum,輸出 shape: (1, B*C, 1, 1)
output = F.conv2d(input_, kernel, groups=B * C)
# reshape 回 (B, C)
return output.reshape(B, C)
print(F_conv2d_approx_mul_reducesum(a,b))
def nn_conv2d_approx_mul_reducesum(a, b):
B, C, H, W = a.shape
# 把 b 變成卷積核,作為每個通道的 filter
kernel = b.reshape(B * C, 1, H, W)
# 輸入 reshape 成 (1, B*C, H, W)
input_ = a.reshape(1, B * C, H, W)
# 假設已有輸入input_和卷積核kernel
# kernel形狀: (輸出通道數, 輸入通道數//groups, 核高, 核寬)
# 例如:groups=B*C時,輸入通道數需為groups的倍數
out_channels = kernel.size(0)
in_channels = kernel.size(1) * (B * C) # 輸入通道數 = 每組通道數 * groups
kernel_size = (kernel.size(2), kernel.size(3))
# 創建nn.Conv2d模塊
conv_layer = nn.Conv2d(
in_channels=in_channels,
out_channels=out_channels,
kernel_size=kernel_size,
groups=B * C,
bias=False # 若F.conv2d未用偏置
)
# 將預定義的kernel賦值給conv_layer的權重
conv_layer.weight.data = kernel # 注意:需確保kernel形狀與nn.Conv2d的weight格式一致
# 深度卷積實現 mul+sum,輸出 shape: (1, B*C, 1, 1)
output = conv_layer(input_)
# reshape 回 (B, C)
return output.reshape(B, C)
print(nn_conv2d_approx_mul_reducesum(a,b))輸出:
tensor([[-0.3991, 0.2382, -8.5925]])
tensor([[-0.3991, 0.2382, -8.5925]])
tensor([[-0.3991, 0.2382, -8.5925]], grad_fn=<ViewBackward0>)可以看到,結果確實一樣。
真正部署時,不太建議這麼做,因為小尺寸沒必要(快不了多少),大尺寸硬件不支持。