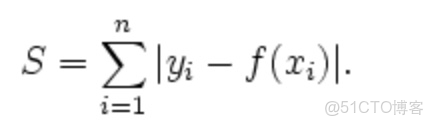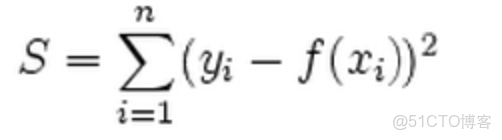前言
L1、L2在機器學習方向有兩種含義:一是L1範數、L2範數的損失函數,二是L1、L2正則化
L1範數、L2範數損失函數
L1範數損失函數:
L2範數損失函數:
L1、L2分別對應損失函數中的絕對值損失函數和平方損失函數
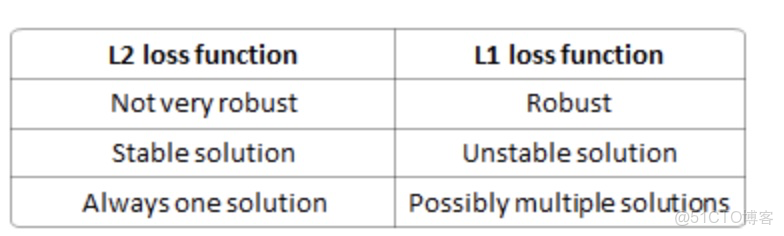
區別:
分析:
robust: 與L2相比,L1受異常點影響比較小,因此穩健
stable: 如果僅一個點,L1就是一個直線,L2是二次,對於直線來説是多解,因此不穩定,而二次函數只有一個極小值點
L1、L2正則化
為什麼出現正則化?
正則化的根本原因是 輸入樣本的丰度不夠,不能涵蓋所有的情況。
解決策略 :
- 對數據源擴充的方法:
輸⼊數據源加上滿⾜⼀定分佈律的噪聲,然後把加上噪聲後的輸⼊源當作“偽”新訓練樣本。
針對圖⽚,還可以採取部分截取、⾓度旋轉等數據增強⼿段,增加“新”樣本。對於詞表,可以增加單詞的近義詞,也能達到類似的效果。
- ⽹絡權值的修正
神經⽹絡的訓練,對某些權值較為敏感。對權值稍微進⾏⼀些修改,訓練的結果可能就迥然不同,所以為了保證⽹絡的泛化能⼒,有必要對權值進⾏修正。具體的做法是,在⽹絡的權值上加上符合⼀定分佈規律的噪聲,然後再重新訓練⽹絡,這樣就增加了整個⽹絡的“抗打擊”能⼒,⽹絡的輸出結果就不會隨數據源的變化⽽有很⼤變動
- 採取“早停”策略
提前停⽌訓練。雖然接着訓練可能會讓訓練誤差變⼩,但讓泛化誤差更⼩,才是我們更⾼的⽬標
- 也可以採用集成方法,訓練多個模型
- dropout
其本質就是通過改變神經⽹絡的結構,⼈為添加⽹絡的不確定性,從⽽鍛鍊神經⽹絡的泛化能⼒。換句話説,通過丟棄部分節點,讓各個⼦⽹絡變得不同
一、L1的出現是為了解決什麼問題?怎麼解決的
L1就是參數的絕對值之和,它的目的就是為了產生一個關於參數w的稀疏矩陣
1、為什麼會產生稀疏矩陣?
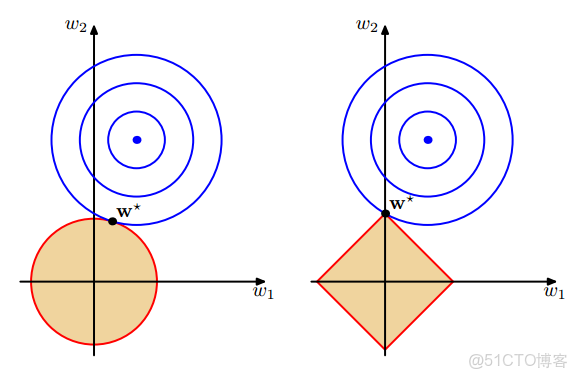
的解限制在黃色區域內,同時使得經驗損失儘可能小
從兩方面解釋,一是直觀解釋,另一種是梯度推導
【直觀解釋】
如上所述,無論是L1,還是L2都可以看成一種條件優化問題,L1所對應的優化區間是個菱形(右圖),L2對應的是個圓形,而最優解就是 等高線與限定區間的交點,對於L1,交點是在座標軸上,對於L2,交點是不在座標軸上,所以L1更容易得到稀疏解。
【梯度解釋】
2、產生稀疏矩陣的目的?
參考:
產生稀疏矩陣的好處可以從特徵選擇來解釋
1)實現特徵的自動選擇
不太理解),但在預測新的樣本時,這些沒用的信息反而會被考慮,從而干擾了對正確yi的預測。所以L1會學習地去掉這些沒有信息的特徵,也就是把這些特徵對應的權重置為0。
二、為什麼會出現L2
L2範數是指向量各元素的平方和然後求平方根。我們讓L2範數的規則項||W||2最小,可以使得W的每個元素都很小,都接近於0,但與L1範數不同,它不會讓它等於0,而是接近於0,這裏是有很大的區別的。而越小的參數説明模型越簡單,越簡單的模型則越不容易產生過擬合現象 。
L2的好處:
1)、防止過擬合,提高泛化能力
不理解)
L1會趨向於產生少量的特徵,而其他的特徵都是0,從而產生稀疏矩陣,自動選擇特徵,而L2會考慮更多的特徵,這些特徵都會接近於0,因此不是稀疏矩陣。
疑問:
1)產生稀疏矩陣好還是不產生稀疏矩陣好,產生稀疏矩陣感覺有點降維的感覺,會選擇有用的特徵?
感覺L2比L1好,因為L2產生的接近於稀疏的矩陣,不是0但接近0,這樣能考慮更多的特徵,而對沒用的特徵不會一棍子打死,只是給一個很小的權重
三、Tensorflow中L1、L2的實現
tf.nn.l2_loss(t, name=None)對t採用l2範式進行計算:output = sum(t ** 2) / 2, t是一維或者多維數組。
tf.add_n([p1, p2, p3....]) 實現列表元素相加,p1, p2, p3分別表示列表
一種顯示的計算:
loss = (tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(
logits=out_layer, labels=tf_train_labels)) +
0.01*tf.nn.l2_loss(hidden_weights) +
0.01*tf.nn.l2_loss(hidden_biases) +
0.01*tf.nn.l2_loss(out_weights) +
0.01*tf.nn.l2_loss(out_biases))#考慮了weight和bias一種隱式的計算:
vars = tf.trainable_variables() //獲取所以的變量
lossL2 = tf.add_n([ tf.nn.l2_loss(v) for v in vars ]) * 0.001 //所有的變量使用l2計算方式累加
//不考慮bias的情況
lossL2 = tf.add_n([ tf.nn.l2_loss(v) for v in vars
if 'bias' not in v.name ])
//把l2損失加入到loss項裏
loss = (tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(
logits=out_layer, labels=tf_train_labels)) +
0.001*lossL2)
L1不可導點如何優化:
1、座標軸下降法
2、近似算法