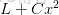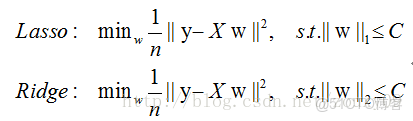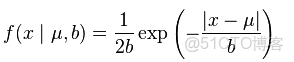1. 簡單列子：

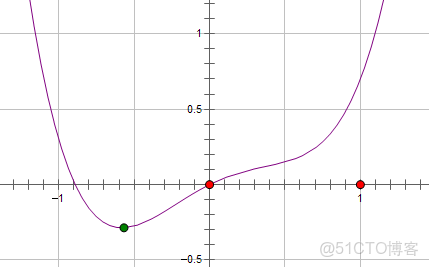
     一個損失函數L與參數x的關係表示為：

           

sklearn linearregression畫出損失函數曲線和曲面_損失函數

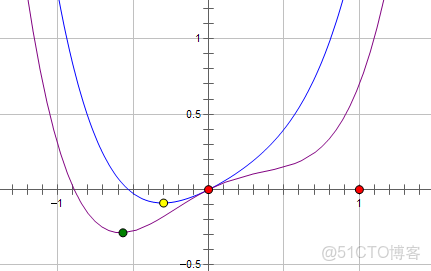
     則 加上L2正則化，新的損失函數L為

sklearn linearregression畫出損失函數曲線和曲面_數據_02

：（藍線）             

sklearn linearregression畫出損失函數曲線和曲面_正則化_03

      最優點在黃點處，x的絕對值減少了，但依然非零。

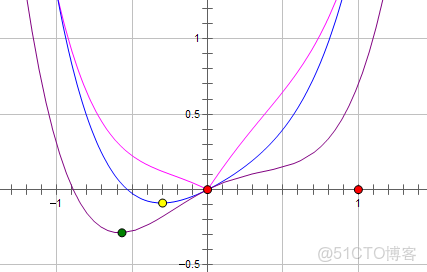
    如果加上L1正則化，新的損失函數L為

sklearn linearregression畫出損失函數曲線和曲面_正則化_04

：（粉線）       

sklearn linearregression畫出損失函數曲線和曲面_數據_05

    最優點為紅點，變為0，L1正則化讓參數的最優值變為0，更稀疏。

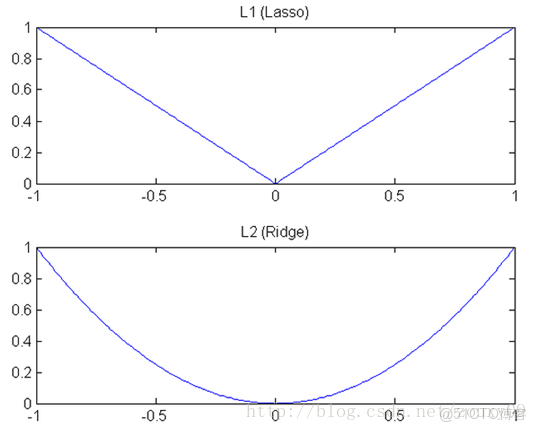
sklearn linearregression畫出損失函數曲線和曲面_損失函數_06

       L1在江湖上人稱Lasso，L2人稱Ridge。

兩種正則化，能不能將最優的參數變為0，取決於最原始的損失函數在0點處的導數，如果原始損失函數在0點處的導數不為0，則加上L2正則化之後（+2Cx），導數依然不為0。而加上L1正則化（導數為-C），如果C大於原先損失函數在0點處的導數的絕對值，x=0就變成了極小值。

2. 概念上理解：

    

sklearn linearregression畫出損失函數曲線和曲面_損失函數_07

加上正則化約束，要達到最小化損失函數，就是不能隨心所欲的取參數的值了，要保證在滿足的限制之內。假設有一個參數，L2的限制條件為|w|^2<c,為上圖的紅線，而L1的限制條件為|w|<c; L1 有角，L2無角

對於L1和L2規則化的代價函數來説，我們可以寫成以下形式：

sklearn linearregression畫出損失函數曲線和曲面_正則化_08

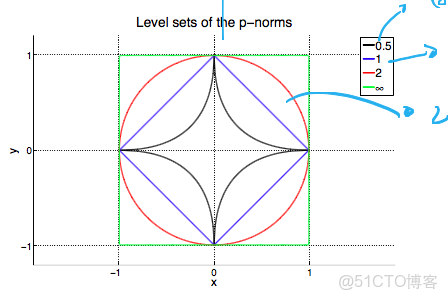
 也就是説，我們將模型空間限制在w的一個L1-ball 中。為了便於可視化，我們考慮兩維的情況，在(w1, w2)平面上可以畫出目標函數的等高線，而約束條件則成為平面上半徑為C的一個 norm ball 。等高線與 norm ball 首次相交的地方就是最優解：

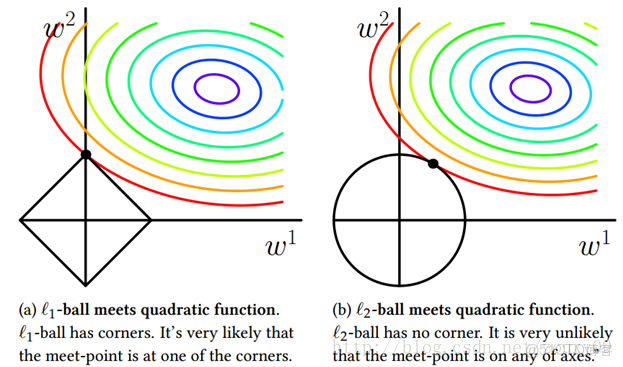
sklearn linearregression畫出損失函數曲線和曲面_正則化_09

可以看到，L1-ball 與L2-ball 的不同就在於L1在和每個座標軸相交的地方都有“角”出現，而目標函數的測地線除非位置擺得非常好，大部分時候都會在角的地方相交。注意到在角的位置就會產生稀疏性，例如圖中的相交點就有w1=0，而更高維的時候（想象一下三維的L1-ball 是什麼樣的？）除了角點以外，還有很多邊的輪廓也是既有很大的概率成為第一次相交的地方，又會產生稀疏性。

       相比之下，L2-ball 就沒有這樣的性質，因為沒有角，所以第一次相交的地方出現在具有稀疏性的位置的概率就變得非常小了。這就從直觀上來解釋了為什麼L1-regularization 能產生稀疏性，而L2-regularization 不行的原因了。

       因此，一句話總結就是：L1會趨向於產生少量的特徵，而其他的特徵都是0，而L2會選擇更多的特徵，這些特徵都會接近於0。Lasso在特徵選擇時候非常有用，而Ridge就只是一種規則化而已。

 

 3. 概率上理解

  如果認為數據是來自高斯密度函數，取對數後就剩一個平方項，這就是L2範式（數據來自高斯分佈，應該在代價函數中加入數據先驗的高斯密度函數---L2範數）

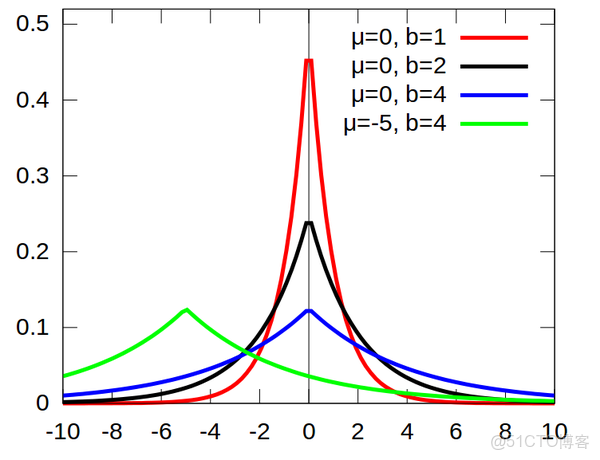
   如果數據稀疏，認為來自於laplace分佈，

 

sklearn linearregression畫出損失函數曲線和曲面_數據_10

laplace數據分佈時稀疏的，laplace概率密度函數

sklearn linearregression畫出損失函數曲線和曲面_損失函數_11

去對數，剩下一個一次項就是L1範式。加入laplace先驗作為正則項的代價函數，説明數據是稀疏的。

L2正則化相當於假設我們所求w的分佈為高斯分佈，L1對應的先驗概率函數為拉普拉斯分佈。 高斯分佈對大w的概率低，對於小w的概率高，所以它限制w到一個小數，但不為0. 拉普拉斯分佈對小w的概率低，希望逼近為0， 對於大w的概率比高斯分佈高。

L1 更 容易稀疏化。

 

 

為什麼正則化能防止過擬合：

過擬合表現在訓練數據上的誤差非常小，而在測試數據上誤差反而增大。其原因一般是模型過於複雜，過分得去擬合數據的噪聲和outliers. 正則化則是對模型參數添加先驗，使得模型複雜度較小，對於噪聲以及outliers的輸入擾動相對較小。

sklearn linearregression畫出損失函數曲線和曲面_正則化_12

 

我們相當於是給模型參數w 添加了一個協方差為1/alpha 的零均值高斯分佈先驗。 對於alpha =0，也就是不添加正則化約束，則相當於參數的高斯先驗分佈有着無窮大的協方差，那麼這個先驗約束則會非常弱，模型為了擬合所有的訓練數據，w可以變得任意大不穩定。alpha越大，表明先驗的高斯協方差越小，模型約穩定， 相對的variance也越小。


因此為了解決過度擬合，有以下兩個辦法。


sklearn linearregression畫出損失函數曲線和曲面_損失函數_13



方法一：儘量減少選取變量的數量

具體而言，我們可以人工檢查每一項變量，並以此來確定哪些變量更為重要，然後，保留那些更為重要的特徵變量。至於，哪些變量應該捨棄，我們以後在討論，這會涉及到模型選擇算法，這種算法是可以自動選擇採用哪些特徵變量，自動捨棄不需要的變量。這類做法非常有效，但是其缺點是當你捨棄一部分特徵變量時，你也捨棄了問題中的一些信息。例如，也許所有的特徵變量對於預測房價都是有用的，我們實際上並不想捨棄一些信息或者説捨棄這些特徵變量。


方法二：正則化

正則化中我們將保留所有的特徵變量，但是會減小特徵變量的數量級（參數數值的大小θ(j)）。

優化目標，也就是説我們需要儘量減少代價函數的均方誤差。因為，如果你在原有代價函數的基礎上加上 1000 乘以 參數這一項 ，那麼這個新的代價函數將變得很大，所以，當我們最小化這個新的代價函數時， 我們將使 參數 的值接近於 0，就像我們忽略了這個值一樣。這種思路就是，如果我們的參數值對應一個較小值的話（參數值比較小），那麼往往我們會得到一個形式更簡單的假設。