PRML Chapter 03 Linear Models for Regression

本章主要介紹了監督學習中的基本模型——線性迴歸模型，即對給定的D D 維輸入，輸出一個或者多個連續的目標變量tt，如第一章介紹的多項式擬合模型即是一種簡單的線性迴歸模型。


  • PRML Chapter 03 Linear Models for Regression
  • Linear Basis Function Models
  • a. Maximum Likelihood and Least Squares
  • b. Geometry of least squares
  • c. Sequential learning
  • d. Regularized least squares
  • e. Multiple outputs
  • The Bias-Variance Decomposition
  • a. Background
  • b. Bias-variance trade-off
  • Bayesian Regression Model
  • a. Parameter distribution
  • b. Predictive distribution
  • c. Equivalent kernel
  • Bayesian Model Comparison
  • The Evidence Approximation
  • a. Evaluation of the evidence function
  • b. Maximizing the evidence function
  • c. Effective number of parameters
  • Code


Linear Basis Function Models

線性迴歸的最基本的模式定義如下，



y(x,ω)=ω0+ω1x1+...+ωDxD(3.1) (3.1) y ( x , ω ) = ω 0 + ω 1 x 1 + . . . + ω D x D

如式(3.1)所示，y(x,ω) y ( x , ω ) 被定義為輸入x x 的線性函數，這在很多時候都無法滿足應用的需求，因為非線性顯然是更常見的狀態。因此，如果我們將式(3.1)中的輸入x x 替換為輸入的函數形式ϕ(x) ϕ ( x ) ，那麼我們則可以得到以下擴展形式，



y(x,ω)=ω0+ω1ϕ1(x1)+...+ωDϕD(xD)=ω0+∑j=1Dωjϕj(x)(3.2) (3.2) y ( x , ω ) = ω 0 + ω 1 ϕ 1 ( x 1 ) + . . . + ω D ϕ D ( x D ) = ω 0 + ∑ j = 1 D ω j ϕ j ( x )

式(3.2)中的函數ϕ(x) ϕ ( x ) 稱為基函數，可以看到，通過使用非線性基函數，y(x,ω) y ( x , ω ) 能夠表示為輸入x x 的非線性函數。然而，我們之所以稱式(3.2)為線性模型，是因為y(x,ω) y ( x , ω ) 是參數ω ω 的線性函數。儘管式(3.2)具有較強的數據擬合能力，但其應用場景也極大的收到了其自身特性的約束，其主要侷限性為，

  • 容易造成維數災難：因為我們假設式(3.2)中的基函數ϕ(x) interval regression_interval regression D 較快增長時，基函數的數量通常隨之成指數級增長；

一般地，我們常用的基函數形式有，

  • 高斯基函數：其中μjμj控制了基函數在輸入空間中的文職，參數s s 控制了基函數的空間大小，

    ϕj(x)=exp{−(x−μj)22s2}(3.3)(3.3)ϕj(x)=exp{−(x−μj)22s2}
  • Sigmoid基函數：

    interval regression_interval regression_02 是logistic sigmoid函數，定義為，

    interval regression_基函數_03

a. Maximum Likelihood and Least Squares

本節主要討論了最大似然函數和最小化平方誤差(最小二乘法)，首先進行概率建模，假設目標值t t 由確定的函數y(x,ω)y(x,ω)給出，其定義如式(3.6)所示，



t=y(x,ω)+ϵ(3.6) (3.6) t = y ( x , ω ) + ϵ

其中，我們定義噪聲ϵ ϵ 是一個零均值的高斯隨機變量，精度(方差的倒數)為β β ，我們可以使用模型式(3.6)中的右側預測值y(x,ω)+ϵ y ( x , ω ) + ϵ 的分佈來描述左側目標值t t ，因此我們有，


p(t|x,ω,β)=(t|y(x,ω),β−1)(3.7)(3.7)p(t|x,ω,β)=N(t|y(x,ω),β−1)

考慮式(3.7)的最大似然形式，定義輸入數據集X={x1,x2,...,xN} X = { x 1 , x 2 , . . . , x N } ，對應的目標值為t1,t2,...tN t 1 , t 2 , . . . t N ，我們把目標向量{tn} { t n } 記作t t ，則有，



p(t|X,ω,β)=∏n=1N(tn|ωTϕ(xn),β−1)(3.8) (3.8) p ( t | X , ω , β ) = ∏ n = 1 N N ( t n | ω T ϕ ( x n ) , β − 1 )

對式(3.8)取對數，可以得到，



lnp(t|ω,β)=∑n=1N(tn|ωTϕ(xn),β−1)=N2lnβ−N2ln(2π)−βED(ω)(3.9) (3.9) l n p ( t | ω , β ) = ∑ n = 1 N N ( t n | ω T ϕ ( x n ) , β − 1 ) = N 2 l n β − N 2 l n ( 2 π ) − β E D ( ω )

其中ED E D 為平方和誤差函數，我們也可以從式(3.8)和(3.9)中看出，線性迴歸模型在噪聲均值為零的情況下，其最大似然等於最小平方誤差，



ED(ω)=12∑n=1N{tn−ωTϕ(x)}2(3.10) (3.10) E D ( ω ) = 1 2 ∑ n = 1 N { t n − ω T ϕ ( x ) } 2

得到最大對數似然的公式(3.8)後，我們則可以通過對參數進行求偏導得到參數的解有，



ωML=(ΦTΦ)−1ΦTt1βML=1N∑n=1N{tn−ωTMLϕ(xn)}2(3.11)(3.12) (3.11) ω M L = ( Φ T Φ ) − 1 Φ T t (3.12) 1 β M L = 1 N ∑ n = 1 N { t n − ω M L T ϕ ( x n ) } 2

其中Φ Φ 定義為一個N∗M N ∗ M 的矩陣，稱為設計矩陣(design matrix)，



⎡⎣⎢⎢⎢ϕ0(x1)⋮ϕ0(xN)⋯⋱⋯ϕM−1(x1)⋮ϕM−1(xN)⎤⎦⎥⎥⎥(3.13) (3.13) [ ϕ 0 ( x 1 ) ⋯ ϕ M − 1 ( x 1 ) ⋮ ⋱ ⋮ ϕ 0 ( x N ) ⋯ ϕ M − 1 ( x N ) ]

若式(3.6)對偏置ω0 ω 0 求偏導，我們可以將式(3.10)演化為式(3.14)，



ED(ω)=12∑n=1N{tn−ω0−∑j=1M−1ωjϕj(xn)}2(3.14) (3.14) E D ( ω ) = 1 2 ∑ n = 1 N { t n − ω 0 − ∑ j = 1 M − 1 ω j ϕ j ( x n ) } 2

並對偏置ω0 ω 0 求偏導，得到，



ω0=t¯−∑j=1M−1ωjϕ¯jt¯=1N∑n=1Ntnϕ¯j=1N∑n=1Nϕj(xn)(3.15)(3.16)(3.17) (3.15) ω 0 = t ¯ − ∑ j = 1 M − 1 ω j ϕ ¯ j (3.16) t ¯ = 1 N ∑ n = 1 N t n (3.17) ϕ ¯ j = 1 N ∑ n = 1 N ϕ j ( x n )

從式(3.15)至(3.17)可以看出，偏置的主要作用是補償訓練集上目標值的均值和基函數均值的加權平均之間的差值。

b. Geometry of least squares

從幾何角度看最小平方和誤差(最小二乘法)，可以考慮一個N N 維空間，它的座標軸由tntn給出，即t={t1...tN}T t = { t 1 . . . t N } T 是這個空間中的一個向量。對於每一個具有M M 個基函數ϕ(x)ϕ(x)的線性迴歸模型y(x,ω) y ( x , ω ) ，其可以看作是一個在N N 維空間中的MM維子空間S S ，因此，函數y(x,ω)y(x,ω)表示子空間S S 中的任意位置。如果把子空間SS看作迴歸函數的預測值空間，而將N N 維tt座標空間視為目標值空間，則最小平方和誤差的目標則是尋找與目標值空間中的目標向量t t 最近的預測值空間中的預測向量y y 。

如下圖所示，我們要在子空間SS中尋找使得距離t t 最近的參數ωω，一般地，我們認為t t 在子空間SS上的正交投影為ω ω 的解。


![這裏寫圖片描述]()


c. Sequential learning

與第二章介紹的一樣，順序學習的主要目的還是解決實時應用與一次計算量過大的問題，這裏我們可以選擇一個數據點或者一小部分數據點，運用隨機梯度下降(stochastic gradient descent)的技術，實現參數的迭代更新。如果誤差函數由數據點的和E=∑nEn E = ∑ n E n 組成，那麼使用隨機梯度下降實現的參數順序學習如下所示，



ω(τ+1)=ω(τ)−η∇En(3.18) (3.18) ω ( τ + 1 ) = ω ( τ ) − η ∇ E n

對於如式(3.10)所示的最小平方和誤差函數，我們可以獲得如下形式的推導，



ω(τ+1)=ω(τ)+η(tn−ω(τ)Tϕn)ϕn(3.19) (3.19) ω ( τ + 1 ) = ω ( τ ) + η ( t n − ω ( τ ) T ϕ n ) ϕ n

d. Regularized least squares

最大似然估計在數據量較小的情況下容易造成過擬合的問題在線性迴歸模型上仍然存在，因此為了降低這種情況，我們使用正則化項，也就是第一章中的懲罰項。即我們可以將誤差函數的形式定義為，



ED(ω)+λEW(ω)(3.20) (3.20) E D ( ω ) + λ E W ( ω )

考慮平方和誤差則有如下形式，



12∑n=1N{tn−ωTϕ(xn)}2+λ2ωTω(3.21) (3.21) 1 2 ∑ n = 1 N { t n − ω T ϕ ( x n ) } 2 + λ 2 ω T ω

對式(3.21)對參數ω ω 求偏導，可以得到參數的解，



ω=(λI+ΦTΦ)−1ΦTt(3.22) (3.22) ω = ( λ I + Φ T Φ ) − 1 Φ T t

與式(3.11)進行相應的比較，會發現式(3.22)多了一個λ λ ，即同樣是最小化誤差函數，加入了正則項後，由於權值λ λ 的作用，會導致基函數ϕ ϕ 的複雜性大大降低，進而實現對過擬合的降低。

e. Multiple outputs

對於多元目標值，一般會有兩種想法，假設對於K K 元目標值(K>0K>0)，

  • 方案一：對於K K 元目標向量中的每一個分量，引入一個不同的基函數集合，即yi(x,ω),i∈1,...,Kyi(x,ω),i∈1,...,K，這樣就變成了多個獨立的線性迴歸問題；
  • 方案二：與方案一不同，方案二中對於所有的分量使用相同的基函數集合，而使用不同的參數，具體的定義y interval regression_基函數_04 1 ，則我們可以有如下的線性迴歸函數形式，

    interval regression_基函數_05 )

The Bias-Variance Decomposition

Linear Basis Function Models部分講到的線性迴歸模型，在現實的應用中往往具有很高的侷限性，其主要表現在以下幾個方面，

  • 最大似然函數的通病，即在有限規模的數據集上訓練複雜模型時，容易造成過擬合的現象；
  • 在線性迴歸函數訓練前，通常都指定了基函數的形式和數量，這很大程度上限制了線性迴歸模型描述數據中有趣的規律的靈活性；
  • 使用正則化項來控制過擬合的主要問題時如何選擇正確的正則化係數λ λ ，從而pick出函數空間中中等複雜程度的模型。

a. Background

因此，為了進一步解決以上線性迴歸模型的以上三個問題，頻率學派和貝葉斯學派分別提出了自己的方法，本節介紹的偏置-方差折中法(bias-variance trade-off)即是一種頻率學派的解決辦法。

在第二章決策論部分，我們定義了損失函數(loss function)為L(t,y(x)) L ( t , y ( x ) ) ，並且採用損失函數的期望式(3.24)來選擇最優的模型，



E[L]=∬L(t,y(x))p(x,t)dxdt(3.24) (3.24) E [ L ] = ∬ L ( t , y ( x ) ) p ( x , t ) d x d t

以使用平方損失函數為例，即L(t,y(x))={y(x)−t}2 L ( t , y ( x ) ) = { y ( x ) − t } 2 ，對誤差函數的期望求偏導，可以得到最優的函數模型h(x) h ( x ) ，具體推導如下，



E[L]=∬{y(x)−t}2p(x,t)dxdt⇒δE[L]δy(x)=2∫{y(x)−t}p(x,t)dt=0⇒h(x)=∫tp(x,t)dtp(x)=∫tp(t|x)dt=Et[t|x](3.25)(3.26)(3.27) (3.25) E [ L ] = ∬ { y ( x ) − t } 2 p ( x , t ) d x d t (3.26) ⇒ δ E [ L ] δ y ( x ) = 2 ∫ { y ( x ) − t } p ( x , t ) d t = 0 (3.27) ⇒ h ( x ) = ∫ t p ( x , t ) d t p ( x ) = ∫ t p ( t | x ) d t = E t [ t | x ]

因此，當我們知道了條件概率分佈p(t|x) p ( t | x ) 後，損失函數即能給出最優的預測結果，如式(3.27)所示。我們可以對式(3.25)的平方項做一些處理，進而得到偏置-方差折中法，



{y(x)−t}2={y(x)−E[t|x]+E[t|x]−t}2={y(x)−E[t|x]}2+2{y(x)−E[t|x]}{E[t|x]−t}+{E[t|x]−t}2(3.28) (3.28) { y ( x ) − t } 2 = { y ( x ) − E [ t | x ] + E [ t | x ] − t } 2 = { y ( x ) − E [ t | x ] } 2 + 2 { y ( x ) − E [ t | x ] } { E [ t | x ] − t } + { E [ t | x ] − t } 2

式(3.28)是對式(3.25)中平方項的一個簡單的擴展，將式(3.28)代入式(3.25)可以得到式(3.29)，交叉項在積分的過程中被消掉，



E[{y(x)−t}2]=∫{y(x)−h(x)}2p(x)dx+∬(h(x)−t)2p(x,t)dxdt(3.29) (3.29) E [ { y ( x ) − t } 2 ] = ∫ { y ( x ) − h ( x ) } 2 p ( x ) d x + ∬ ( h ( x ) − t ) 2 p ( x , t ) d x d t

上式可以看作是預測函數y(x) y ( x ) 與最優函數h(x) h ( x ) 之間的偏差(即兩者之間的相似程度)，加上最優函數與目標值之間的方差(即最優函數在目標值附近的波動)。

b. Bias-variance trade-off

對於偏置-方差折中法，一般考慮使用參數ω ω 控制的函數y(x,ω) y ( x , ω ) 對h(x) h ( x ) 建模，

  • 貝葉斯學派：從貝葉斯的觀點來看，模型y(x,ω) interval regression_線性迴歸_06 的情況下，對每一個數據集訓練出一個函數和其相應的平方損失值，對所有的數據集上得到的函數進行平均來評估模型。

從以上兩派人馬的觀點可以看出，其核心思想都是通過平均來降低過擬合的程度，貝葉斯利用的是參數ω ω 的平均，而頻率觀點採用數據集上的平均。因此，與式(3.29)類似，對應於每一個數據集 D 有，



ED[{y(x;)−h(x)}2]={ED[y(x;)]−h(x)}2(bais)2+ED[{y(x;)−ED[y(x,)]}2]variance(3.30) (3.30) E D [ { y ( x ; D ) − h ( x ) } 2 ] = { E D [ y ( x ; D ) ] − h ( x ) } 2 ⏟ ( b a i s ) 2 + E D [ { y ( x ; D ) − E D [ y ( x , D ) ] } 2 ] ⏟ v a r i a n c e

對比式(3.29)和(3.30)，(3.30)無非就是對多個數據集進行了一下平均。式(3.30)的第一項表示所有數據集得出的平均預測與最優模型h(x) h ( x ) 之間的差異即平方偏置(bias)；第二項則度量了對於單個數據集，單個模型給出的解在平均值附近的波動，這被稱為方差(variance)。

現在我們可以看一下式(3.30)用以降低過擬合的原理，對於數據集上的損失均值(3.30)，很顯然，我們的目標是要使其最小化，

  • 情況一：當偏差趨近於零時，意味着各數據集上訓練得到的模型平均後與最優模型基本吻合，這時往往就是過擬合了，方差部分因為過擬合的模型無法擬合每一個數據集，因此便會產生較大的損失，造成式(3.30)無法達到最小值；
  • 情況二：當方差趨近於零時，意味着每一個數據集上訓練得到的模型都差別不大，這顯然是發生了欠擬合，因此偏差就會成倍增加。

綜合以上兩種極端情況，可以看出偏置-方差折中的原理，即通過最小化約束來互相懲罰。然而這一方法也具有很大的侷限性，主要表現在其依賴於所有數據集的平均，而實際應用中，往往不存在多個數據集，即使存在也會對其合併，使用更大規模的數據訓練複雜模型效果會更好。

Bayesian Regression Model

基於以上傳統的最大似然的侷限性，貝葉斯方法通常是引入參數的先驗分佈，並利用貝葉斯定理計算後驗分佈在先驗分佈上的平均，從而解決，

  • 問題一：使用最大似然的線性迴歸模型，往往需要根據特定的應用確定合適的模型複雜度的問題；
  • 問題二：最大似然函數的過擬合問題；
  • 問題三：降低因引入正則項而增加的計算量。

a. Parameter distribution

在偏置-方差折中的方法裏，主要考慮的是預測函數y(x,ω) y ( x , ω ) 中參數ω ω 的點估計，而貝葉斯方法考慮參數ω ω 的全分佈，因此，我們可以定義參數ω ω 服從均值為m0 m 0 、協方差S0 S 0 的高斯分佈，



p(ω)=(ω|m0,S0)(3.31) (3.31) p ( ω ) = N ( ω | m 0 , S 0 )

給定數據集的目標值t t ，我們在式(3.7)定義了似然函數p(t|ω) p ( t | ω ) ，進而可以得到相應的後驗分佈，



p(ω|t)=(ω|mN,SN)mN=SN(S−10m0+βΦTt)S−1N=S−10+βΦTΦ(3.32)(3.33)(3.34) (3.32) p ( ω | t ) = N ( ω | m N , S N ) (3.33) m N = S N ( S 0 − 1 m 0 + β Φ T t ) (3.34) S N − 1 = S 0 − 1 + β Φ T Φ

以上即為基於貝葉斯方法的線性迴歸函數參數分佈的基本形式，在PRML中，為了簡化討論，考慮參數分佈為均值為零的高斯分佈，並且分佈由精度參數α α 控制，



p(ω|α)=(ω|0,α−1I)(3.35) (3.35) p ( ω | α ) = N ( ω | 0 , α − 1 I )

這樣後驗分佈中mN、S−1N m N 、 S N − 1 也會發生相應的變化。考慮後驗分佈(3.32)的最大似然，我們稱之為最大後驗分佈(Maximum A Posteriori)，對其取對數的結果如下，



lnp(ω|t)=−β2∑n=1N{tn−ωTϕ(xn)}2−α2ωTω+const(3.34) (3.34) l n p ( ω | t ) = − β 2 ∑ n = 1 N { t n − ω T ϕ ( x n ) } 2 − α 2 ω T ω + c o n s t

將式(3.34)與基於最大似然估計的式(3.14)相比，會發現最大後驗比最大似然多了一個參數ω ω 的二次項，這顯然與加入正則項的最大似然一致。

b. Predictive distribution

在實際應用中，更常用到的是預測分佈，即給定新的輸入值x x 預測出新的t t ，其具體形式如下，


p(t|t,α,β)=∫p(t|ω,β)p(ω|t,α,β)dω(3.35)(3.35)p(t|t,α,β)=∫p(t|ω,β)p(ω|t,α,β)dω

參數

含義

t

t

訓練數據集中的目標值集合

α

α

參數ω

ω 的控制參數，來自先驗(3.35)

β

β

似然函數(3.7)的控制參數，定義為高斯分佈的精度

因為式(3.57)中的兩項均為高斯分佈，因此我們可以把預測分佈表示為，



p(t|x,t,α,β)=(t|mTNϕ(x),σ2N(x))δ2N(x)=1β+ϕ(x)TSNϕ(x)(3.36)(3.37) (3.36) p ( t | x , t , α , β ) = N ( t | m N T ϕ ( x ) , σ N 2 ( x ) ) (3.37) δ N 2 ( x ) = 1 β + ϕ ( x ) T S N ϕ ( x )

式(3.37)中的第一項取自似然函數(3.7)，被定義為精度，可以看作是數據中的噪聲；第二項與先驗(3.35)有關，其反映了預測分佈與參數ω ω 關聯的不確定性。很顯然的，當我們觀測到足夠多的數據時，預測分佈的結果與最大似然類似，這樣，我們的先驗起的作用將很小，即式(3.37)僅僅只由數據中的噪聲β β 控制。

c. Equivalent kernel

等價核可以看作一種非參數的訓練方法。考慮式(3.33)，如果採用零均值先驗的參數分佈即m0=0 m 0 = 0 ，則式(3.33)變為，



mN=βSNΦt(3.38) (3.38) m N = β S N Φ t

將式(3.38)代入式(3.2)，則有，



y(x,mN)=mTNϕ(x)=∑n=1Nβϕ(x)TSNϕ(xn)tn(3.39) (3.39) y ( x , m N ) = m N T ϕ ( x ) = ∑ n = 1 N β ϕ ( x ) T S N ϕ ( x n ) t n

其中SN S N 由式(3.34)定義，因此在點x x 處的預測均值由訓練機目標變量tn t n 的線性組合給出，



y(x,mN)=∑n=1Nk(x,xn)tnk(x,xn)=βϕ(x)TSNϕ(x′)(3.40)(3.41) (3.40) y ( x , m N ) = ∑ n = 1 N k ( x , x n ) t n (3.41) k ( x , x n ) = β ϕ ( x ) T S N ϕ ( x ′ )

式(3.41)的k(x,xn) k ( x , x n ) 函數被稱為平滑矩陣(smoother matrix)或者等價核(equivalent kernel)。對於式(3.40)，我們可以認為等價核描述的是新輸入值x x 與已有數據集中數據點xn x n 之間的距離，而y(x,mN) y ( x , m N ) 則是數據點的目標值tn t n 與這一距離的加權平均。比較常見的方法比如K K 最近鄰。

Bayesian Model Comparison

貝葉斯模型比較(Bayesian Model Comparison)是貝葉斯學派看待模型複雜度的方法論，即通過概率來表示模型選擇的不確定性，對每一個模型，利用其整個參數分佈上對數據集的擬合程度反應其優先級。假設我們有LL個模型{i} { M i } ，其中i=1,...,L i = 1 , . . . , L 。對於給定數據集 D 和模型的先驗p(i) p ( M i ) ，我們定義其後驗分佈為，



p(i|)∝p(i)p(|i)(3.42) (3.42) p ( M i | D ) ∝ p ( M i ) p ( D | M i )

對於式(3.42)，先驗分佈p(i) p ( M i ) 用於描述不同模型之間的優先級。模型證據(model evidence) p(|i) p ( D | M i ) ，可以看作是模型空間上的似然函數，因此也被稱為邊緣似然(marginal likelihood)，它表達了考慮數據擬合能力後的模型優先級，描述了從一個模型生成一個數據集 D 的概率。

  • 模型選擇(model selection)：對於模型求平均來選擇模型可以簡單的近似為使用最有可能的一個模型作為預測。

interval regression_線性迴歸_07

使用以上的模型選擇思想，可以對模型證據進行相應的近似選擇，考慮使用一個參數ω ω 控制模型證據，



p(|i)=∫p(|ω,i)p(ω|i)dω(3.43) (3.43) p ( D | M i ) = ∫ p ( D | ω , M i ) p ( ω | M i ) d ω

通過考慮參數ω ω 的近似，我們可以更清楚的認識到模型證據的性質並選擇出更優的模型，



p(ω|,i)=p(|ω,i)p(ω|i)p(|i)(3.45) (3.45) p ( ω | D , M i ) = p ( D | ω , M i ) p ( ω | M i ) p ( D | M i )

考慮每一個模型僅有一個參數ω ω ，由式(3.5)可知p(ω|,i)∝p(|ω,i)p(ω|i) p ( ω | D , M i ) ∝ p ( D | ω , M i ) p ( ω | M i ) ，對於似然函數p(|ω,i) p ( D | ω , M i ) ，我們考慮使用最有可能的ωMAP ω M A P 來近似，



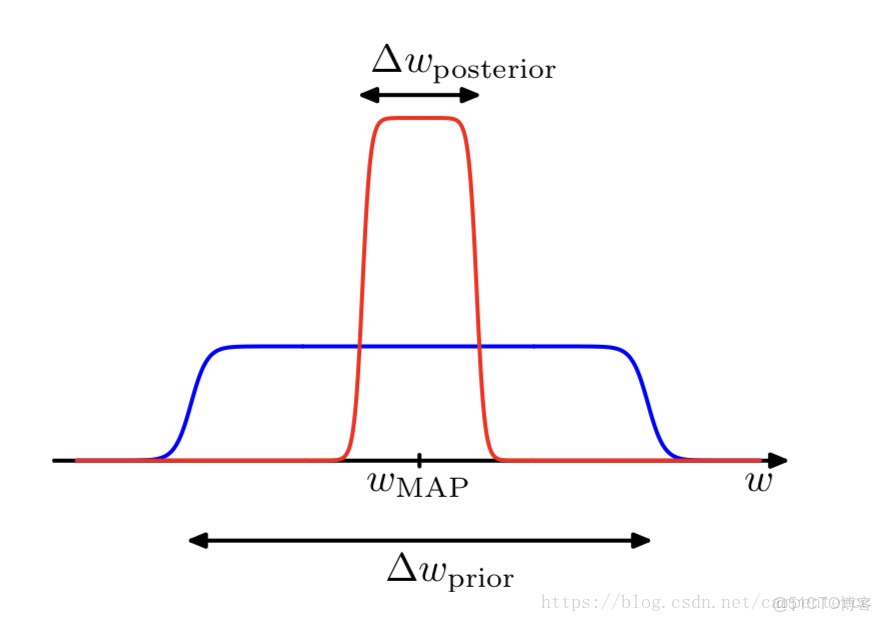
∫p(|ω,i)dω≃p(|ωMAP,i)∗Δωposteriori(3.46) (3.46) ∫ p ( D | ω , M i ) d ω ≃ p ( D | ω M A P , M i ) ∗ Δ ω p o s t e r i o r i

如圖所示，式(3.46)對ω ω 的積分近似為對尖峯ωMAP ω M A P 與Δωposterior Δ ω p o s t e r i o r 的乘積。類似地，我們可以對先驗分佈p(ω|i) p ( ω | M i ) 進行相同的近似，對於平坦的寬度為Δωprior Δ ω p r i o r 的先驗分佈，其p(ω|i)=1Δωprior p ( ω | M i ) = 1 Δ ω p r i o r ，因此式(3.43)可以表示為，式(3.44)簡化了所有的i M i ，



p()=∫p(|ω)p(ω)dω≃1Δωprior∫p(|ω)dω≃p(|ωMAP)∗ΔωposteriorΔωprior(3.47) (3.47) p ( D ) = ∫ p ( D | ω ) p ( ω ) d ω ≃ 1 Δ ω p r i o r ∫ p ( D | ω ) d ω ≃ p ( D | ω M A P ) ∗ Δ ω p o s t e r i o r Δ ω p r i o r

對式(3.47)求對數可以得到，



lnp()≃lnp(|ωMAP)+ln(ΔωposteriorΔωprior)(3.48) (3.48) l n p ( D ) ≃ l n p ( D | ω M A P ) + l n ( Δ ω p o s t e r i o r Δ ω p r i o r )

類似地，對於多個參數(M>0 M > 0 )，有



lnp()≃lnp(|ωMAP)+M∗ln(ΔωposteriorΔωprior)(3.49) (3.49) l n p ( D ) ≃ l n p ( D | ω M A P ) + M ∗ l n ( Δ ω p o s t e r i o r Δ ω p r i o r )

對於式(3.48)和式(3.49)中的第一項可以理解為最優參數下模型對於數據的擬合程度，而第二項作為懲罰項，當Δωposterior Δ ω p o s t e r i o r 變小時，即參數更加接近數據時，ln(ΔωposteriorΔωprior) l n ( Δ ω p o s t e r i o r Δ ω p r i o r ) 會變成一個很小的負數，從而達到懲罰的效果，顯然，我們的目標是最大化(3.48)或者(3.49)，即最大化模型對數據的擬合程度。

以上便是從貝葉斯角度，對模型複雜度的理解，以及模型選擇中對過擬合的判別。

The Evidence Approximation

a. Evaluation of the evidence function

純粹的貝葉斯處理方法中，通常會引入超參數α α 和β β 的先驗分佈，然後通過對超參數以及參數ω ω 求積分的方式做預測。但實際情況是，我們可以解析的求出對參數ω ω 的積分，或者解析的求出對參數α α 、β β 的積分；卻無法對所有的這些參數解析的求得，因此，定義一種近似方法，

  • 證據近似(evidence approximation)：首先獲取到超參數的近似形式，再利用該近似對參數ω ω 求積分。證據近似在統計學的文獻中也被稱為經驗貝葉斯(empriccal Bayes)、第二類最大似然(type2 maximum likelihood)、或者推廣的最大似然(generalized maximum likelihood)。

如果引入α α 和β β 的超參數先驗分佈，那麼預測分佈可以通過ω、α、β ω 、 α 、 β 求積分的方式獲得，式(3.50)省略了對輸入x x 的以來，tt表示多個樣本的目標值t t ，而tt表示一個樣本的多元目標值，



p(t|t)=∭p(t|ω,β)p(ω|t,α,β)p(α,β|t)dωdαdβ(3.50) (3.50) p ( t | t ) = ∭ p ( t | ω , β ) p ( ω | t , α , β ) p ( α , β | t ) d ω d α d β

由於無法解析的求得所有參數的解，證據近似的方法告訴我們可以找到後驗分佈p(α,β|t) p ( α , β | t ) 的近似解α̂  α ^ 和β̂  β ^ ，由此，式(3.50)表示的預測分佈就可以近似為，



p(t|t)≃p(t|t,α̂ ,β̂ )=∫p(t|ω,β̂ )p(ω|t,α̂ ,β̂ )dω(3.51) (3.51) p ( t | t ) ≃ p ( t | t , α ^ , β ^ ) = ∫ p ( t | ω , β ^ ) p ( ω | t , α ^ , β ^ ) d ω

因此，我們只需要求得α α 、β β 的近似α̂  α ^ 、β̂  β ^ 即可，而由貝葉斯定理可知，p(α,β|t) p ( α , β | t ) 服從，



p(α,β|t)∝p(t|α,β)p(α,β)(3.52) (3.52) p ( α , β | t ) ∝ p ( t | α , β ) p ( α , β )

在證據框架中，我們可以通過最大化邊緣似然函數p(t|α,β) p ( t | α , β ) 得到α̂  α ^ 、β̂  β ^ 。

對於邊緣似然分佈p(t|α,β) p ( t | α , β ) ，通過全職參數進行積分可以得到，即



p(t|α,β)=∫p(t|ω,β)p(ω|α)dω(3.53) (3.53) p ( t | α , β ) = ∫ p ( t | ω , β ) p ( ω | α ) d ω

對於線性迴歸模型，由式(3.9)、(3.10)、(3.35)可得，



p(t|α,β)=(β2π)N2(α2π)M2π∫exp{−E(ω)}dω(3.54) (3.54) p ( t | α , β ) = ( β 2 π ) N 2 ( α 2 π ) M 2 π ∫ e x p { − E ( ω ) } d ω

其中E(ω) E ( ω ) 可以看作是正則化的平方和誤差函數，如果不考慮一些比例常數的話。通過對參數ω ω 配平方，可以得到，



E(ω)=E(mN)+12(ω−mN)TA(ω−mN)(3.55) (3.55) E ( ω ) = E ( m N ) + 1 2 ( ω − m N ) T A ( ω − m N )

其中，



A=αI+βΦTΦE(mN)=β2||t−ΦmN||2+β2mTNmNmN=βA−1ΦTt(3.56)(3.57)(3.58) (3.56) A = α I + β Φ T Φ (3.57) E ( m N ) = β 2 | | t − Φ m N | | 2 + β 2 m N T m N (3.58) m N = β A − 1 Φ T t

對於式(3.54)的邊緣似然函數，其對數形式定義為，



lnp(t|α,β)=M2lnα+N2lnβ−E(mN)−12ln|A|−N2ln(2π)(3.59) (3.59) l n p ( t | α , β ) = M 2 l n α + N 2 l n β − E ( m N ) − 1 2 l n | A | − N 2 l n ( 2 π )

式(3.59)即為證據函數的表達式。

b. Maximizing the evidence function

最大化證據函數的主要目的式根據式(3.59)求出超參數α α 、β β 的最佳近似α̂  α ^ 、β̂  β ^ 。首先定義式(3.60)的特徵向量方程，



(βΦTΦ)μi=λiμi(3.60) (3.60) ( β Φ T Φ ) μ i = λ i μ i

由式(3.56)可知A A 的特徵值為α+λi α + λ i ，則對於式(3.59)中的ln|A| l n | A | 對於α α 求導，



ddαln|A|=ddαln∏i(λi+α)=ddα∑iln(λi+α)=∑i1λi+α(3.61) (3.61) d d α l n | A | = d d α l n ∏ i ( λ i + α ) = d d α ∑ i l n ( λ i + α ) = ∑ i 1 λ i + α

因此式(3.59)對α α 求偏導可得，



α=γmTNmNγ=∑iλiα+λi(3.62)(3.63) (3.62) α = γ m N T m N (3.63) γ = ∑ i λ i α + λ i

類似地，我們可以使式(3.59)對β β 求偏導，進而得到，



1β=1N−γ∑n=1N{tn−mTNϕ(xn)}2(3.64) (3.64) 1 β = 1 N − γ ∑ n = 1 N { t n − m N T ϕ ( x n ) } 2

c. Effective number of parameters

式(3.62)定義了超參數α α 的值，這一值通過式(3.53)中的先驗分佈p(ω|α) p ( ω | α ) 控制着參數ω ω 的分佈，考慮式(3.63)，顯然有λiλi+α λ i λ i + α 位於0到1之間，因此式(3.63)中0≤γ≤M 0 ≤ γ ≤ M 。對α α 的值的影響則主要分為兩種情況，

  • 情況一：λi≫α interval regression_ide_08 將會與最大似然值接近。
  • 情況二：λi≪α interval regression_ide_09 也會接近於0。

由於以上兩種情況，我們可以利用γ γ 很好的度量先驗分佈p(ω|α) p ( ω | α ) 中的參數數量。

Code

https://github.com/zhoudinglive/PRML_exercise