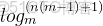一、樹
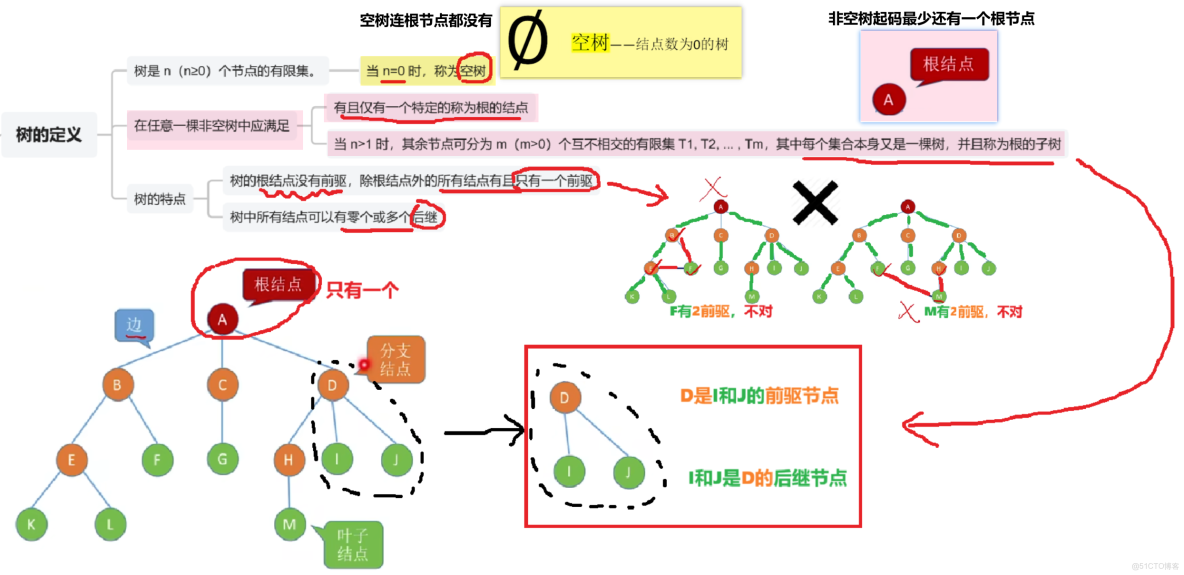
1、樹的定義
計算機專業的應該都學過,只需要略微回顧一下這些名詞就行;跨考的看一下這個思維導圖應該也能理解
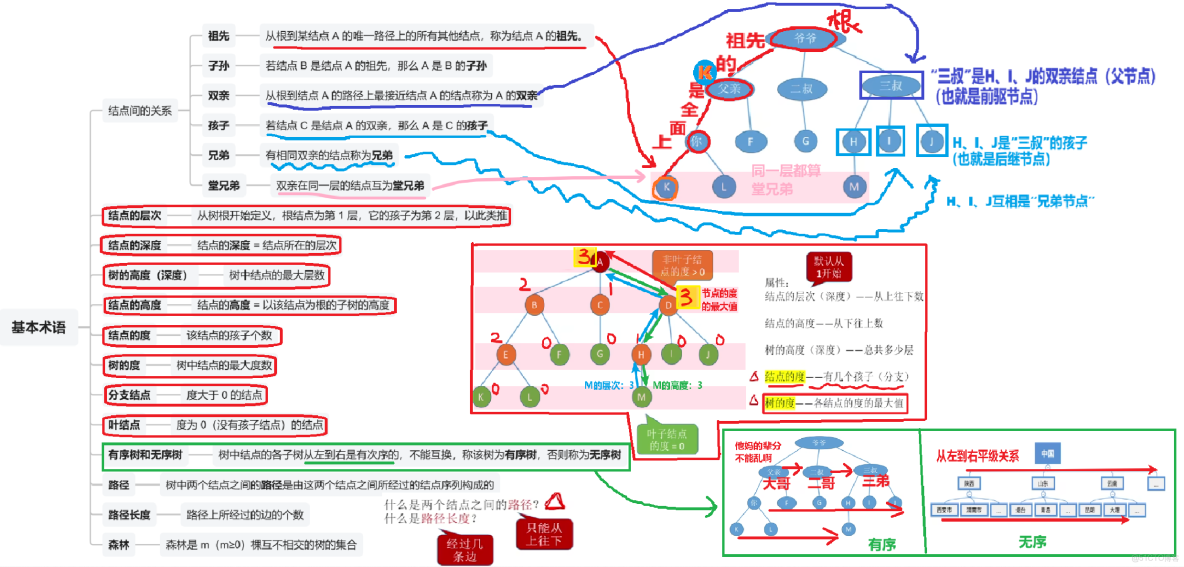
2、其他基本術語
放大來看,過一遍就行,都是很基礎的概念
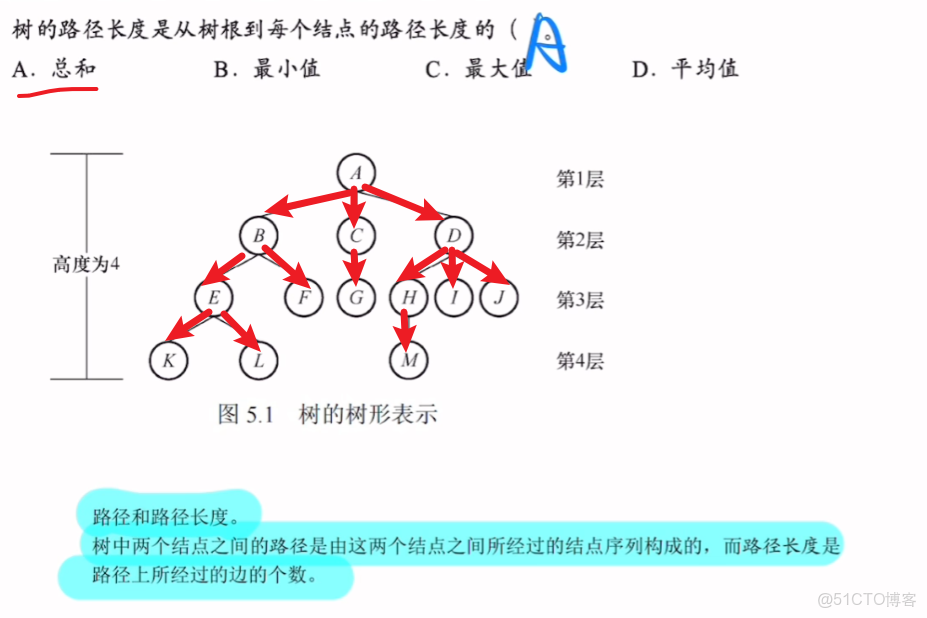
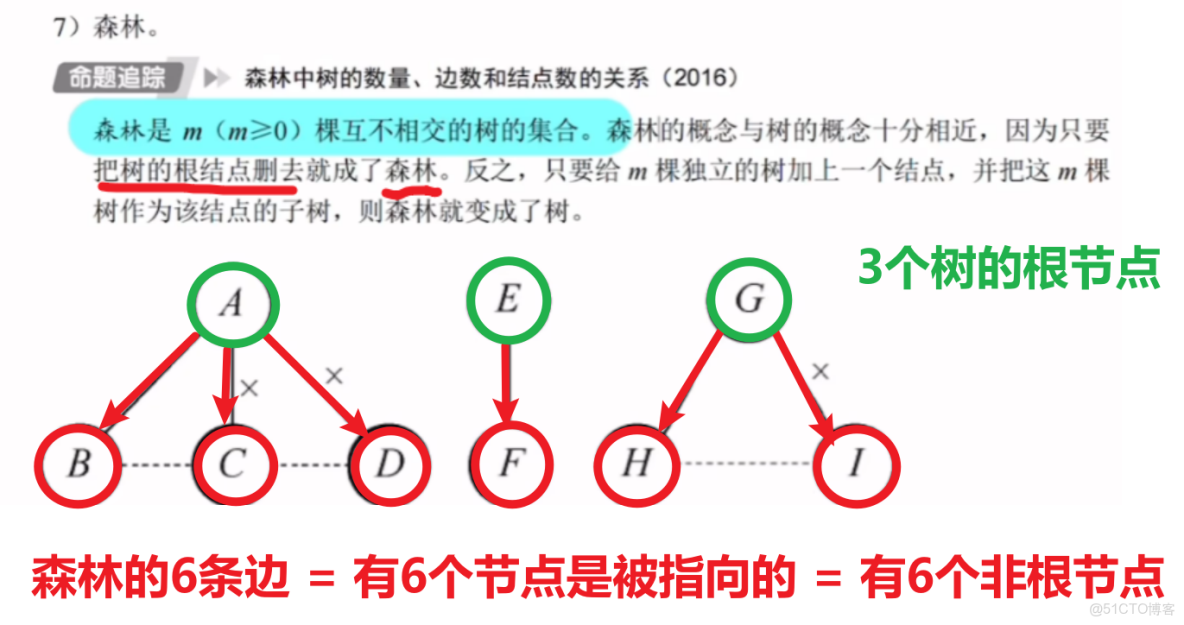
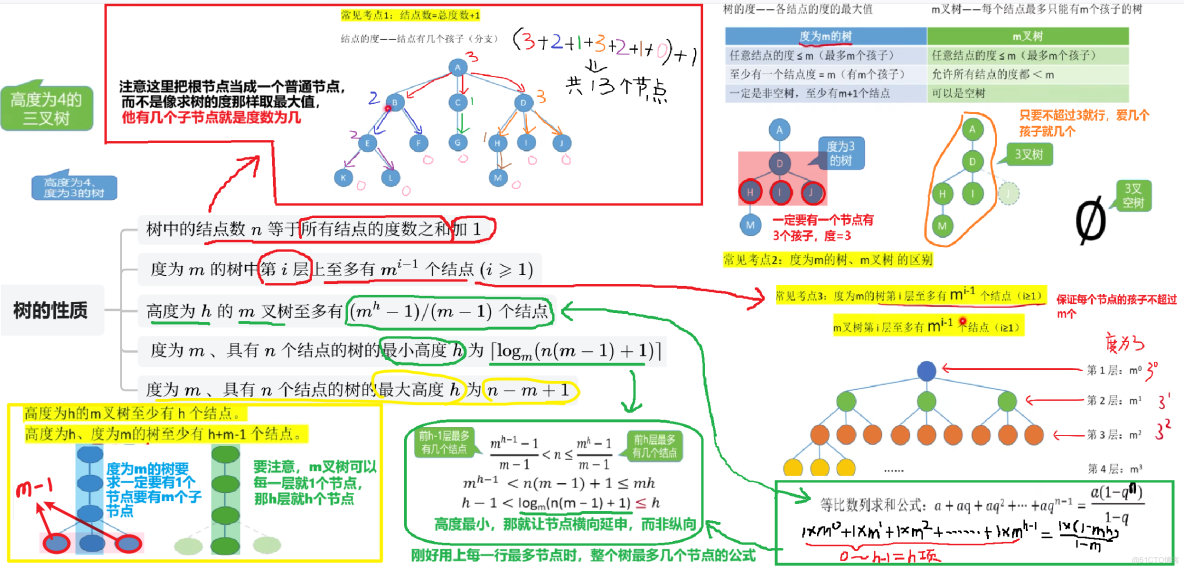
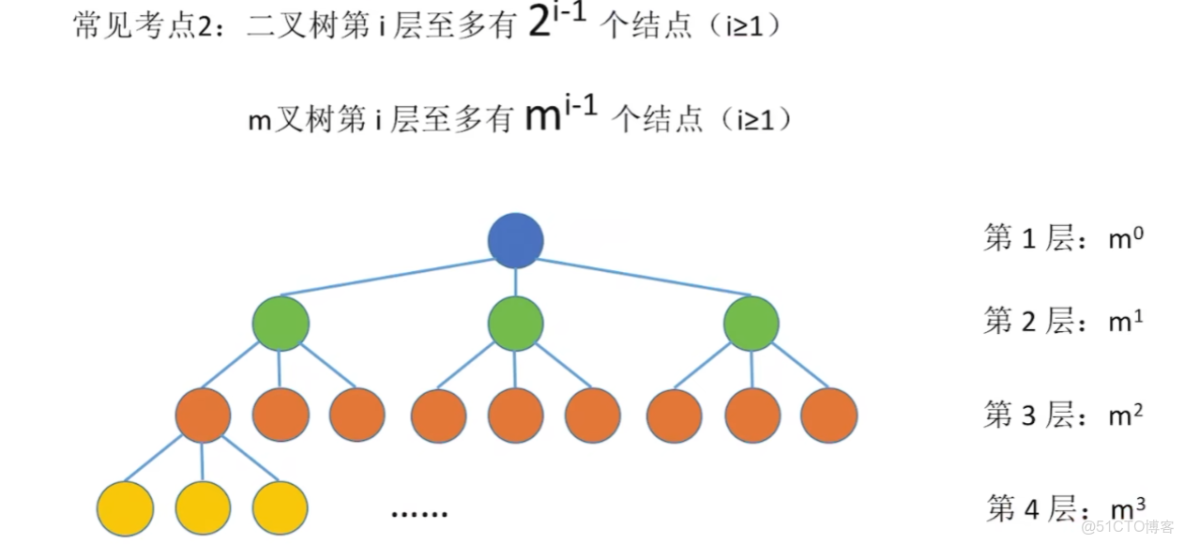
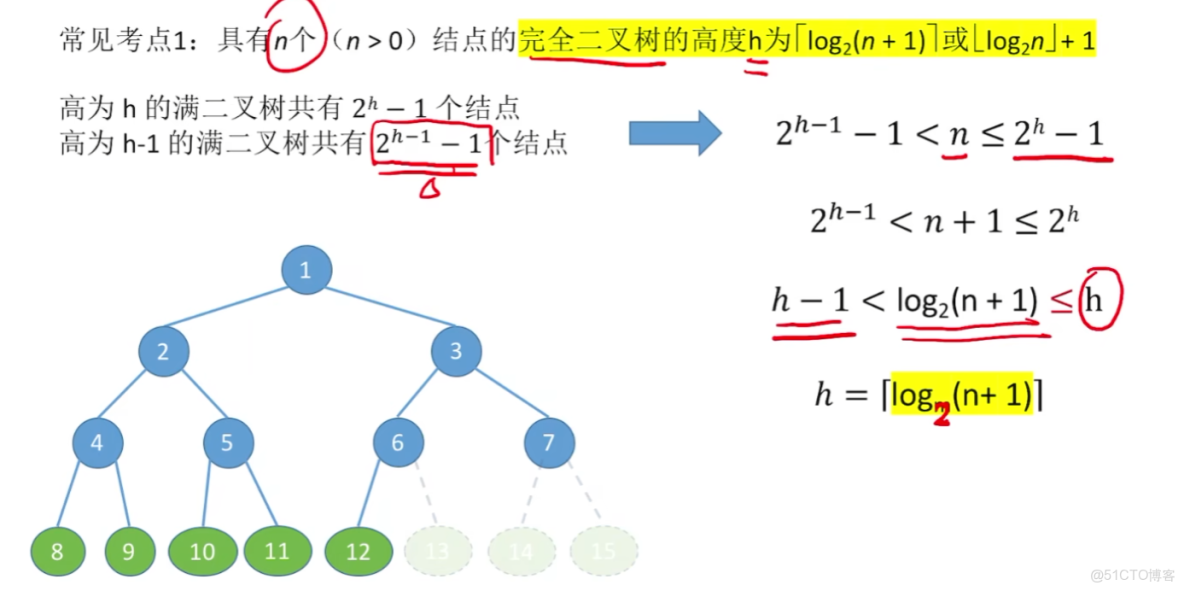
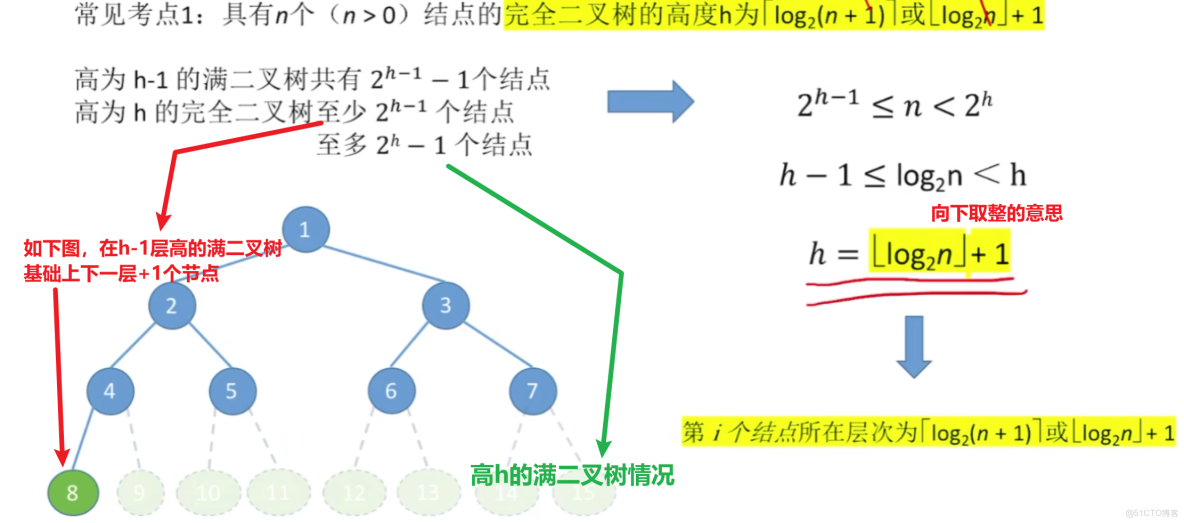
3、樹的常考性質計算
雖然我的圖畫的很醜。。。但是我覺得這些性質不需要花太多圖和文筆來解釋,就這麼幾個公式概念之間用一個圖集合起來,應該都看得懂吧。。。?
;
;
【重點注意!!】
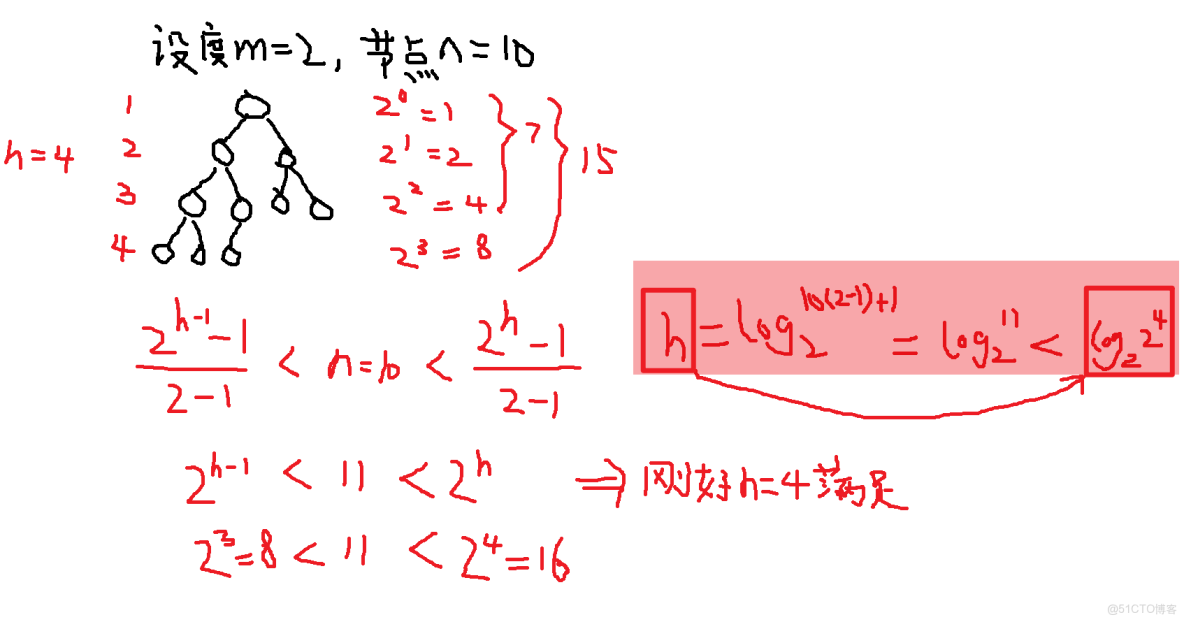
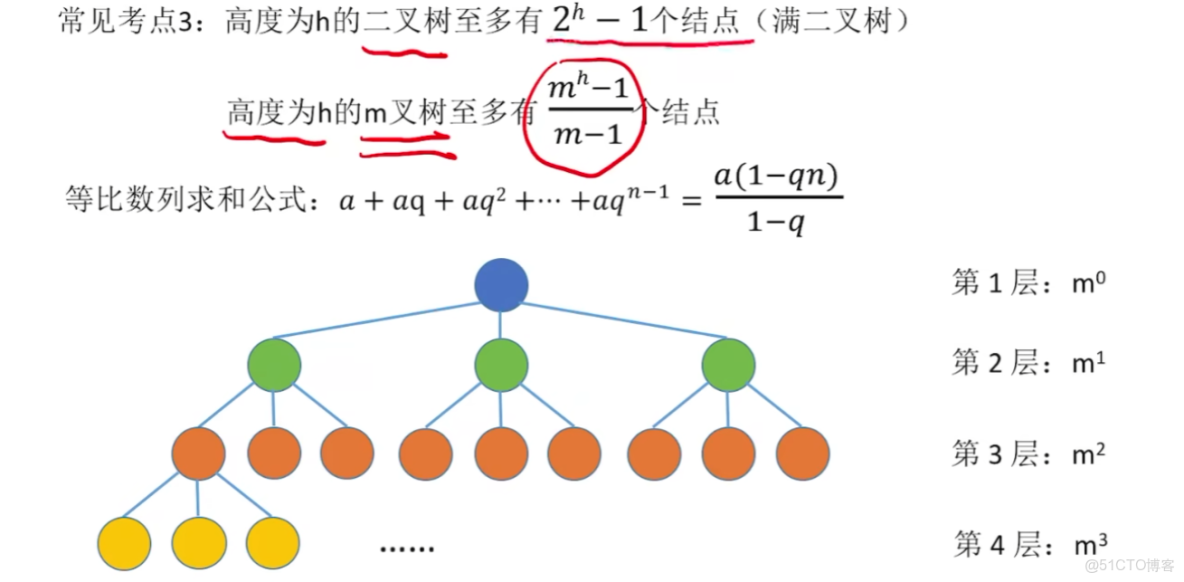
1、已知度為m、節點共n個,【最小高度h】一定一定要取到【超出
的第1個結果】,或者按照下面這個公式理解,我也不知道怎麼解釋反正記住就行
;
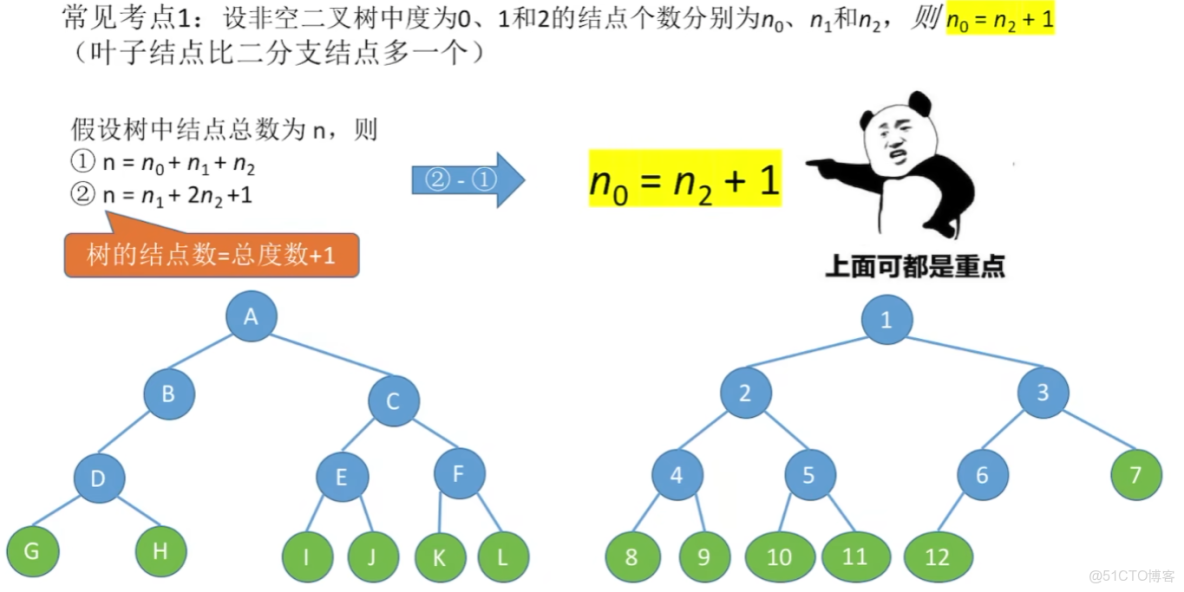
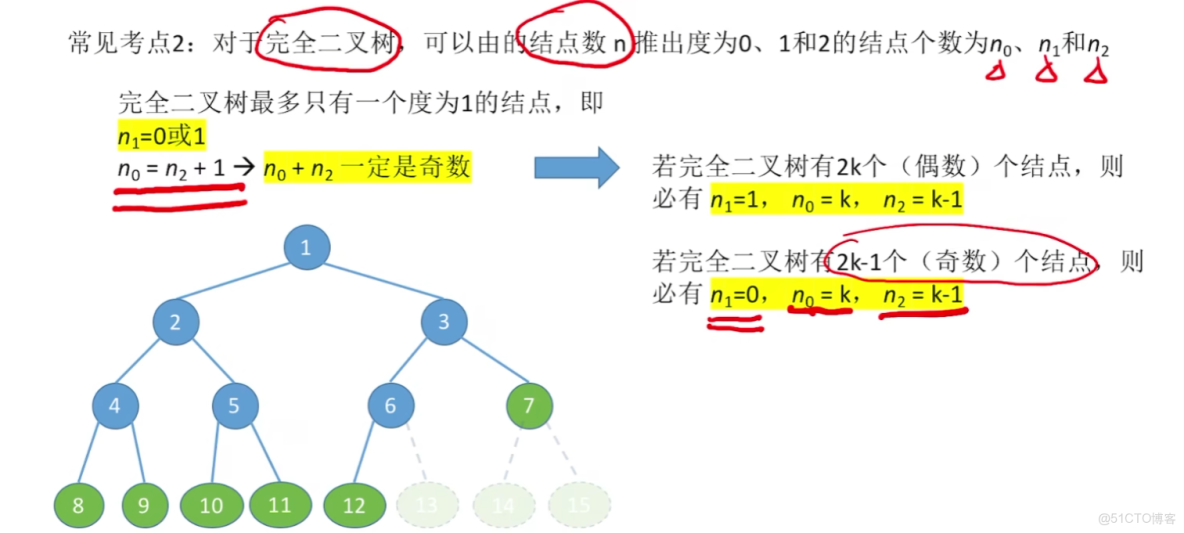
2、已知各個度數節點有幾個,求總結點數的【2種平替計算公式】!!!!
4、【總結】
5、【例題】
二、二叉樹
1、二叉樹的定義
就是每個節點最多有【2棵子樹】的樹,或者説最多有【2個分支】
- 當然是【最多】,沒説【一定】,【啥節點也沒有的空樹】也是一種【子樹】
- 依舊是狗屎圖,需要各位放大,不過也沒什麼知識點,只是要注意區分一下【二叉樹】和【度為2的樹】二者的區別
2、特殊二叉樹
這個思維導圖我就不亂畫了,先仔細回憶一下
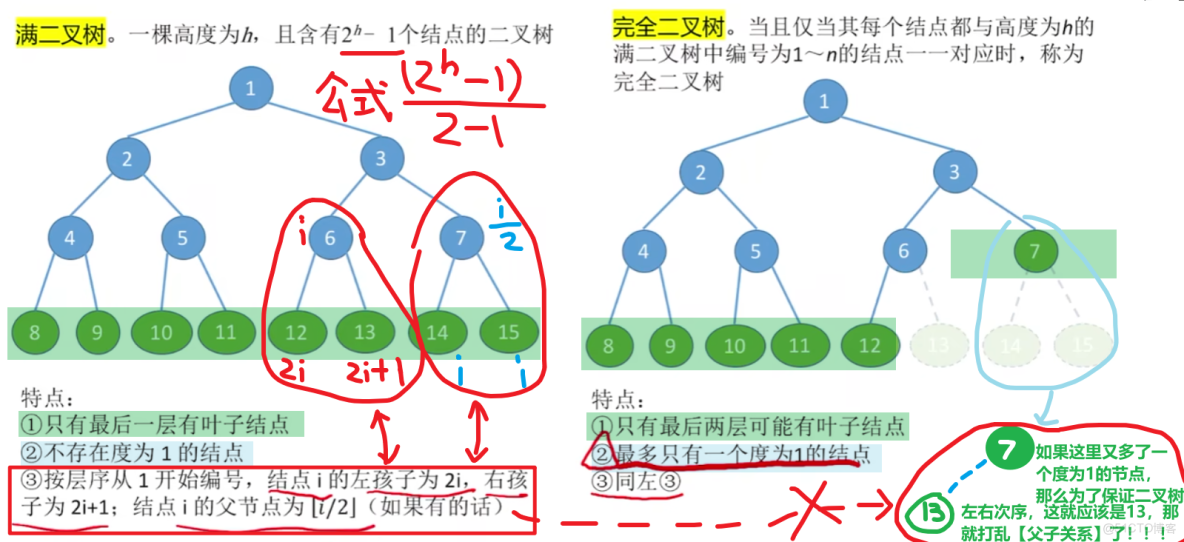
1)【滿二叉樹】和【完全二叉樹】
【滿二叉樹】一定是【完全二叉樹】,但是【完全二叉樹】不一定是【滿二叉樹】
2)二叉排序樹
3)平衡二叉樹
3、二叉樹的性質
;
;
我懶得打字解釋了,全部都可以按前面【樹的性質】推算,只要牢記【二叉樹的度<=2】就行了(一般按度數m=2計算就可以了)
;
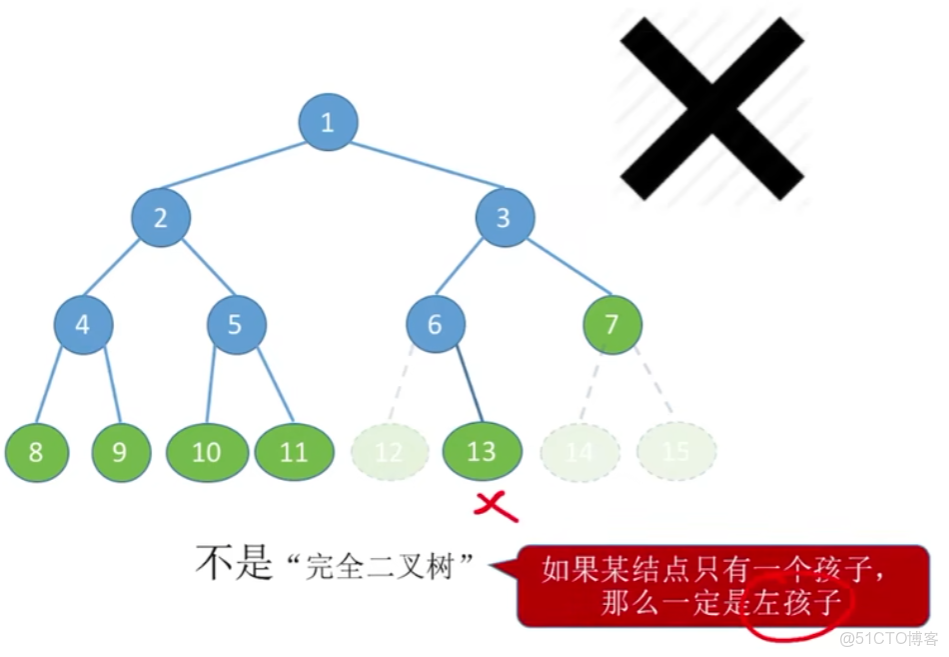
【留意一下:完全二叉樹】
【例題】
4、二叉樹的存儲結構(感覺出的題很少,應該非重點)
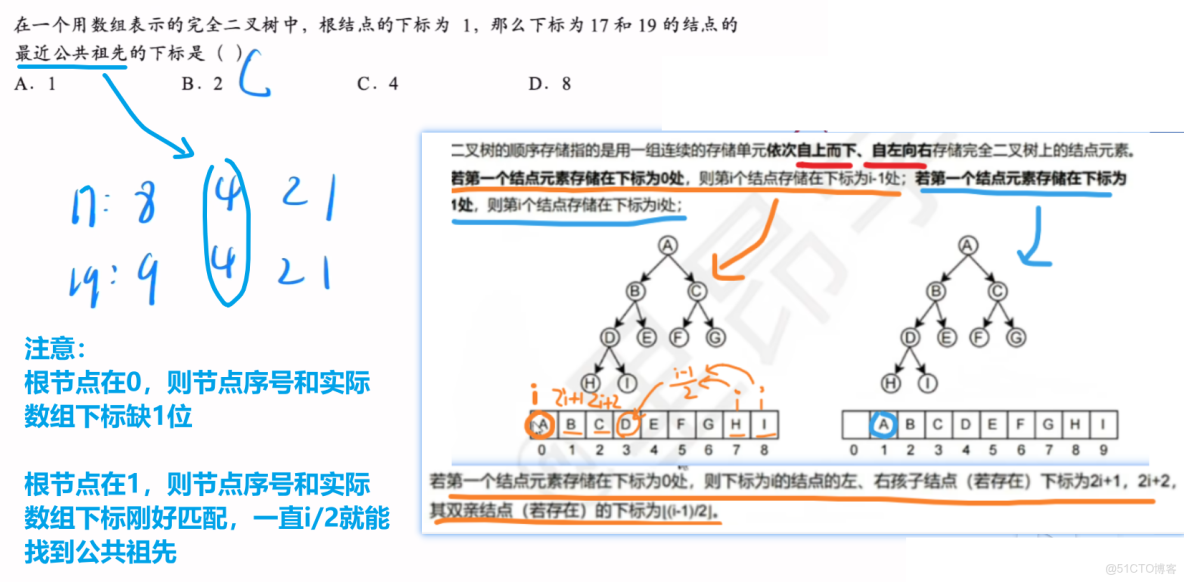
1)第一種:順序存儲
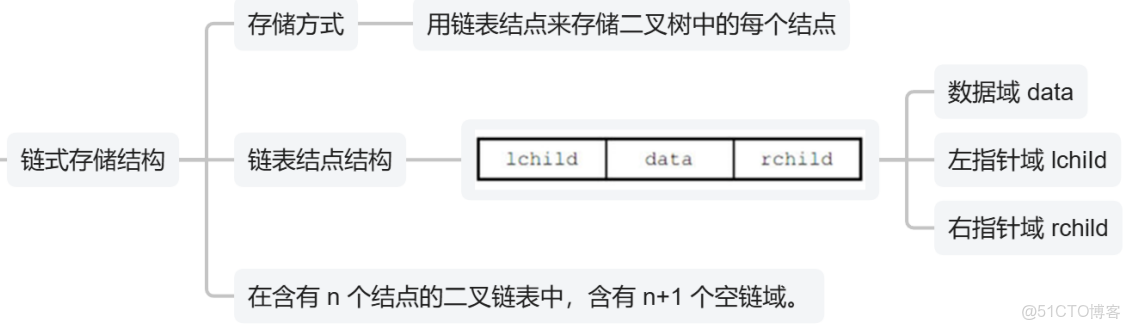
2)第二種:鏈式存儲
;
【注意考點!!】
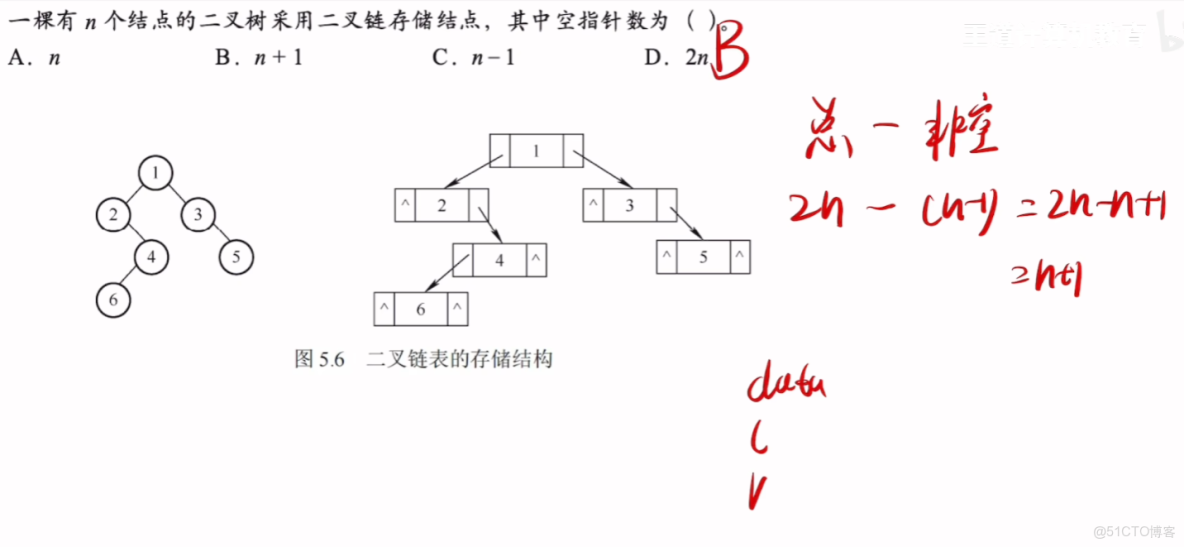
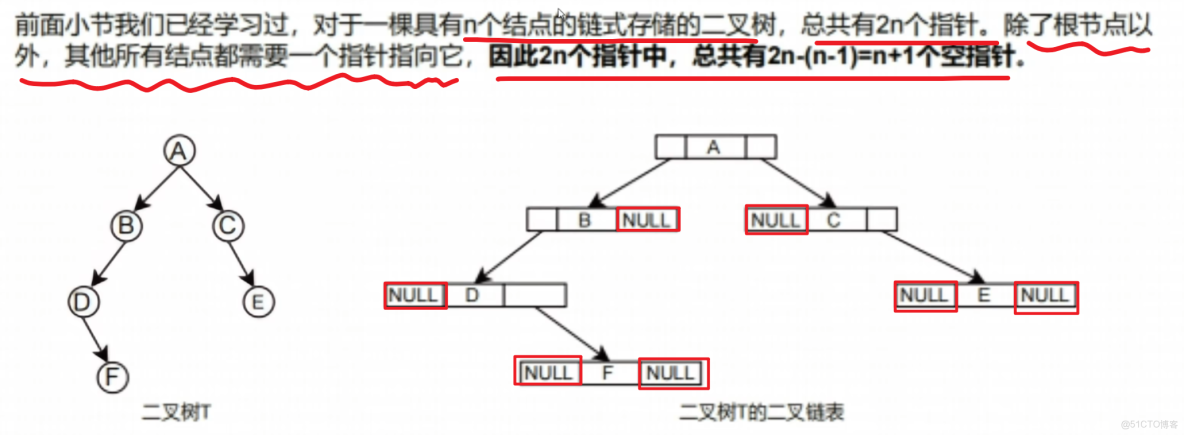
- 【二叉樹二指針】情況的【指針數】
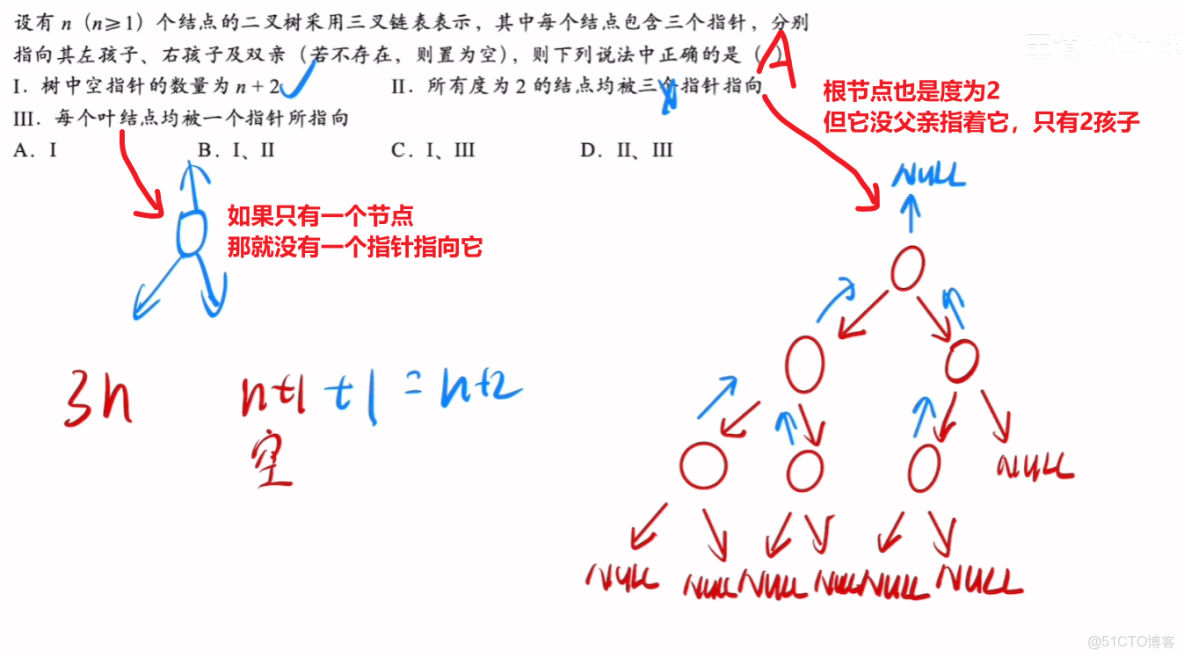
- 【二叉樹三指針】情況的【指針數】
【例題】
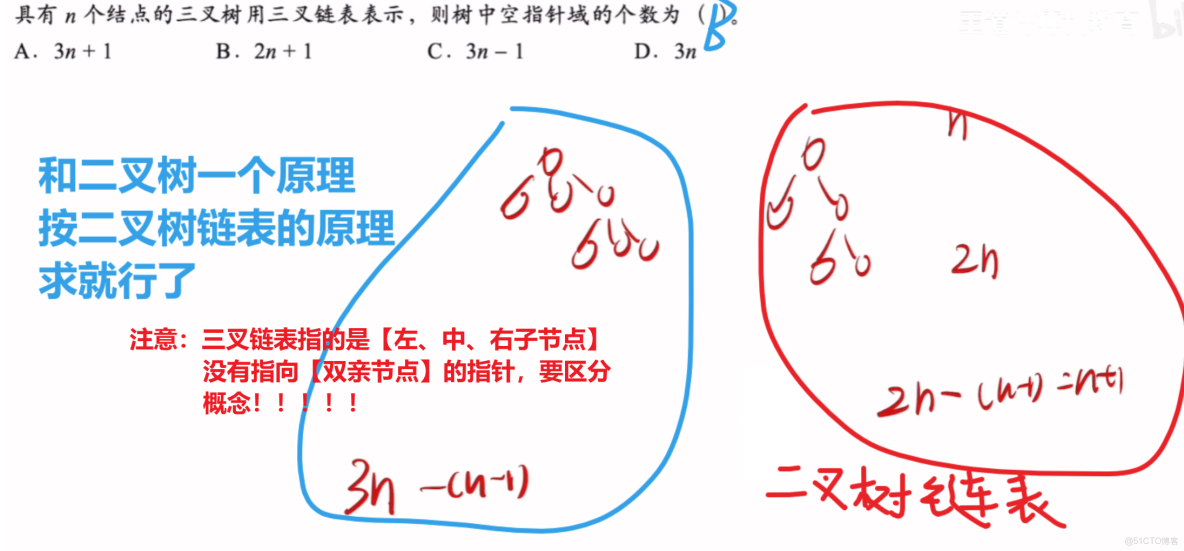
【三叉樹用三叉鏈表】不等於【二叉樹用三指針鏈表】!!!!
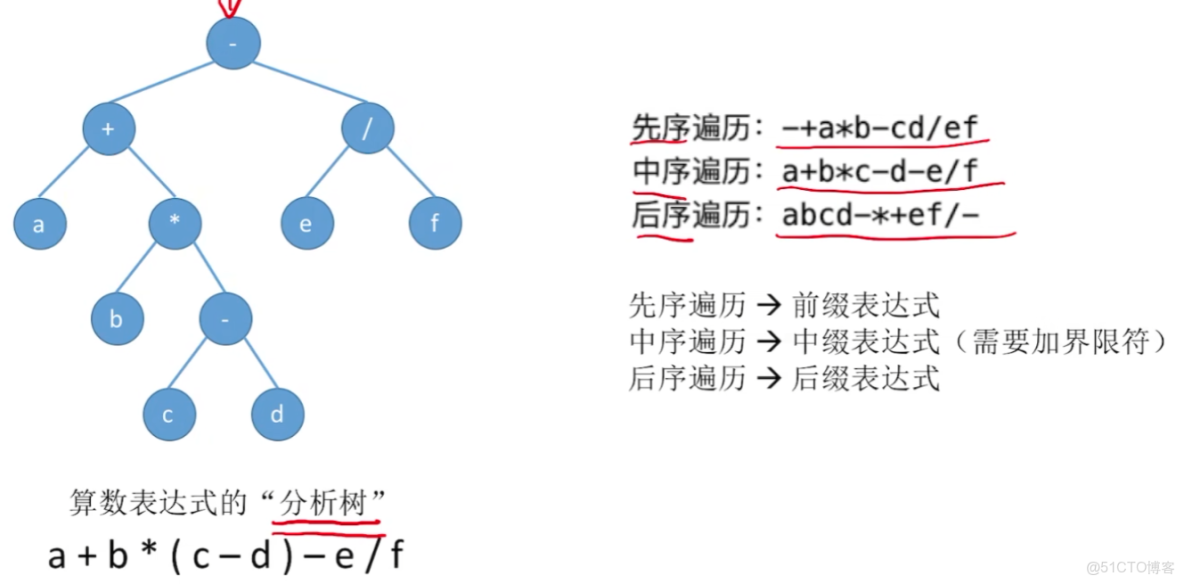
5、二叉樹的遍歷(常考)
【三大類遍歷的總結】
1)先序遍歷【根左右】
2)中序遍歷【左根右】
3)後序遍歷【左右根】
4)層次遍歷
5)由遍歷序列構造二叉樹
【先序 + 後序】
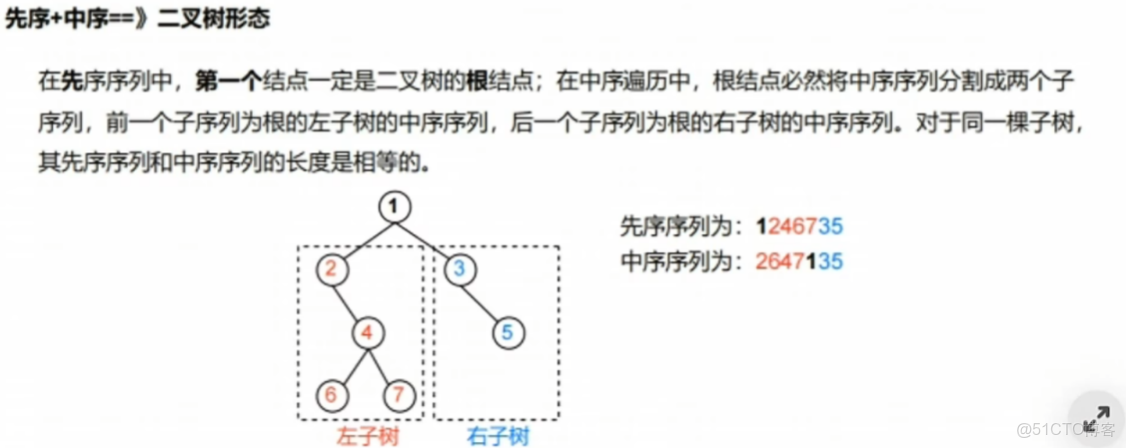
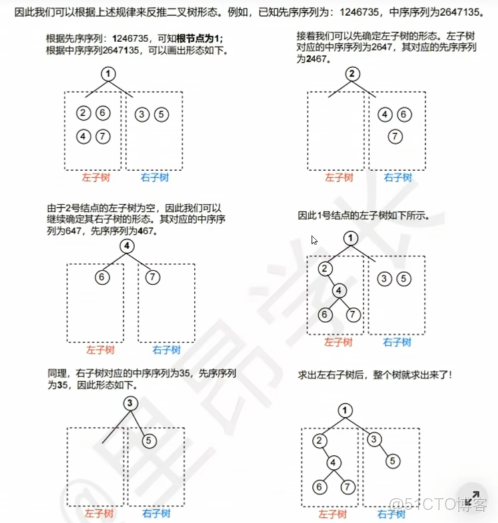
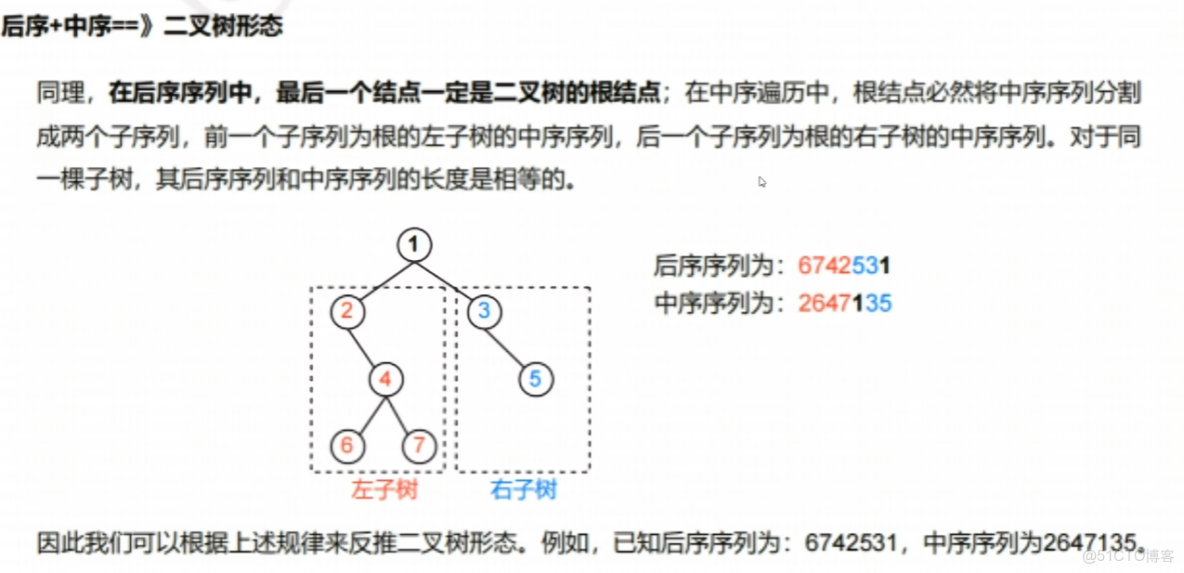
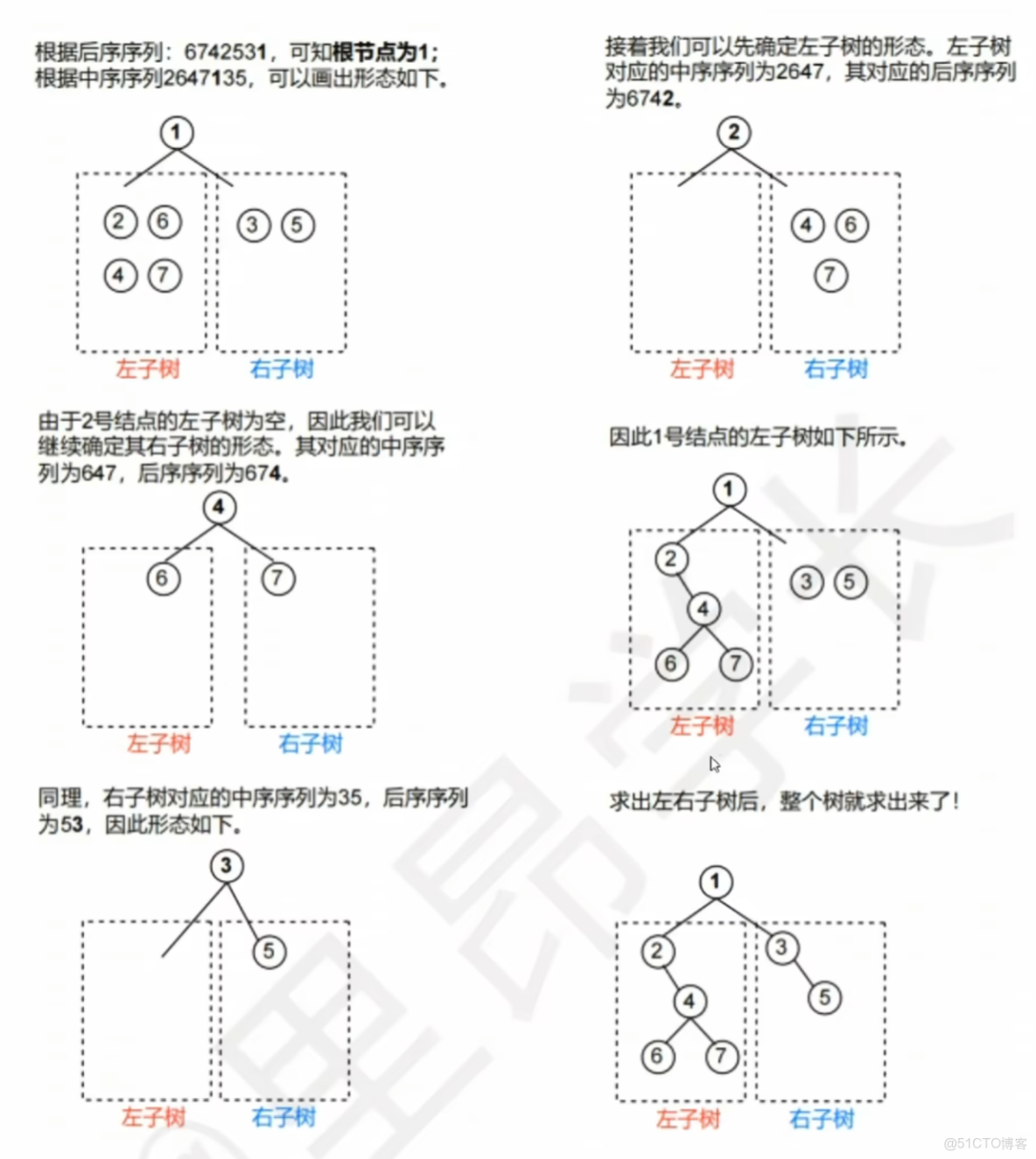
【後序+中序】
;
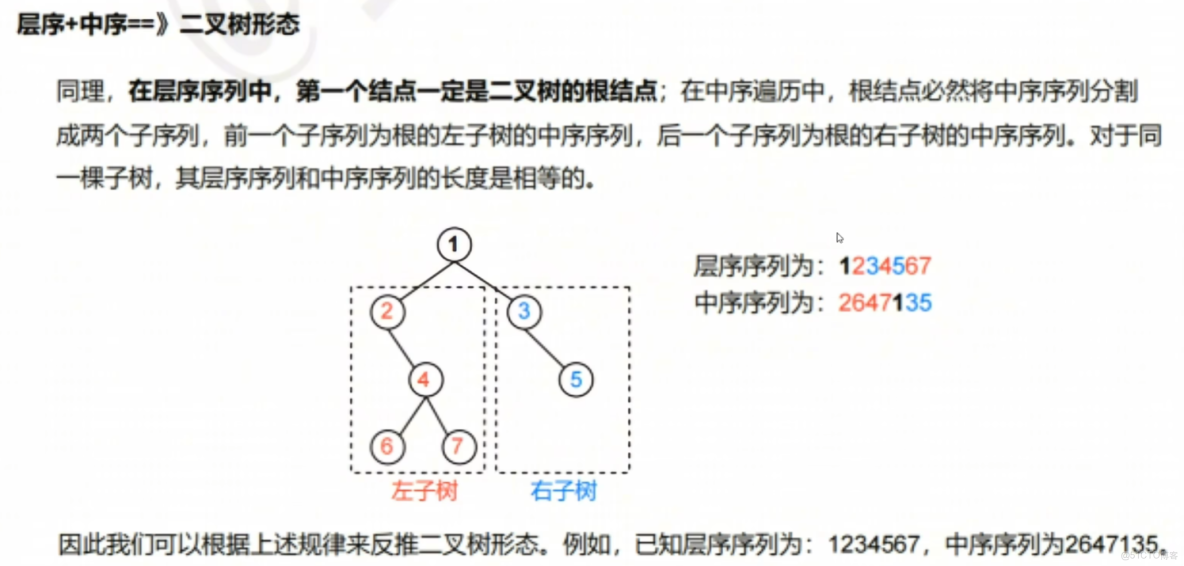
【層序+中序】
;
;
【一些技巧知識點】
- 【先序遍歷】和【後序遍歷】完全不一樣:該樹的節點只有1左孩子、或只有1右孩子
- 【中序遍歷】對於“節點只有1左孩子、或只有1右孩子”的樹,【子樹根】只會在序列最前、或最後
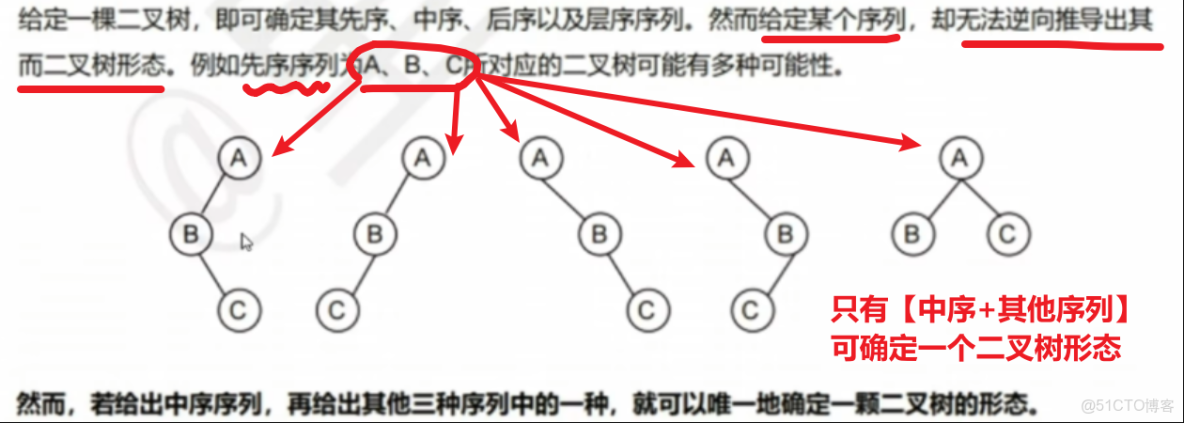
- 【只有前序、後序】時,並非什麼也推不出
- 可以推出【根節點】、以及【緊挨根節點的左、右孩子】
- 【任何遍歷方式】輸出了【N個元素的序列】,都對應有【】種二叉樹形狀
- 也可以用【卡特蘭數】來計算【n個節點的二叉樹形狀】
- 什麼情況【先序=中序】、【後序=中序】
【例題】
三、線索二叉樹
【總結思維導圖】
【具體解釋】
1)中序線索二叉樹
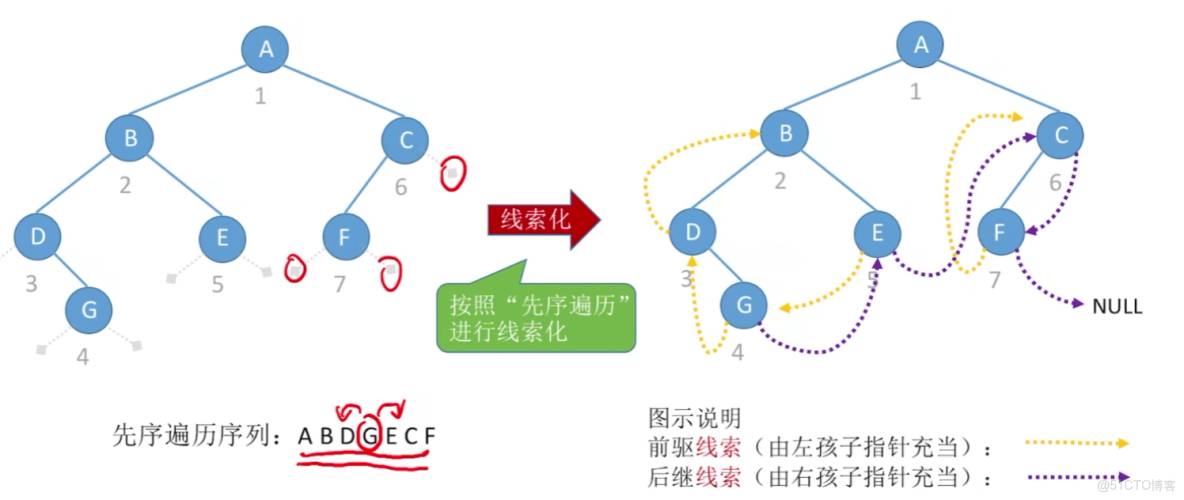
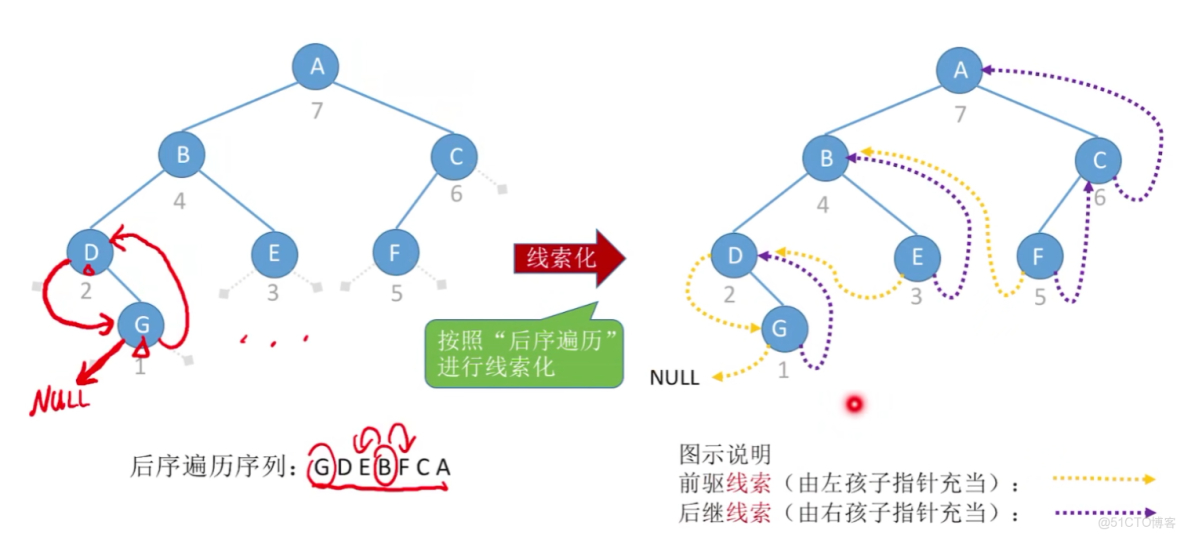
2)先序 和 後序線索二叉樹
【先序遍歷線索二叉樹】
【後續遍歷線索二叉樹】