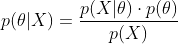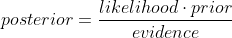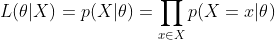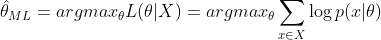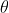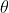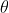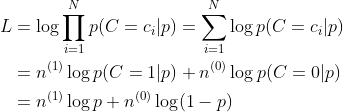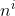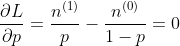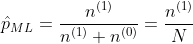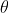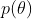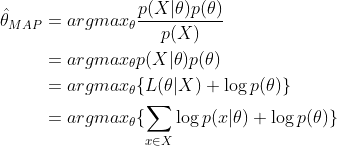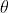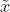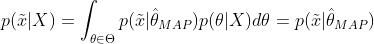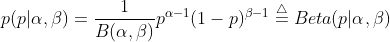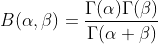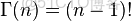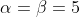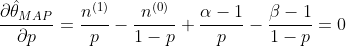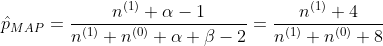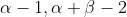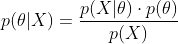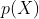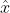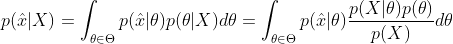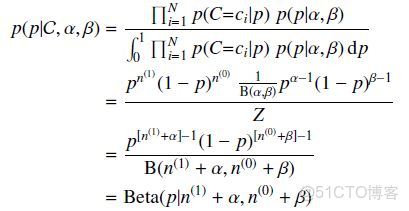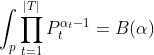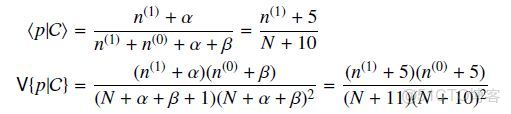機器學習中的參數估計方法

本文主要介紹文本分析的三類參數估計方法-最大似然估計MLE、最大後驗概率估計MAP及貝葉斯估計，以及三者之間的區別。

1、最大似然估計MLE

首先回顧一下貝葉斯公式

這個公式也稱為逆概率公式，可以將後驗概率轉化為基於似然函數和先驗概率的計算表達式，即

最大似然估計就是要用似然函數取到最大值時的參數值作為估計值，似然函數可以寫做

由於有連乘運算，通常對似然函數取對數計算簡便，即對數似然函數。最大似然估計問題可以寫成

這是一個關於

的函數，求解這個優化問題通常對

求導，得到導數為0的極值點。該函數取得最大值是對應的

的取值就是我們估計的模型參數。

以扔硬幣的伯努利實驗為例子，N次實驗的結果服從二項分佈，參數為P，即每次實驗事件發生的概率，不妨設為是得到正面的概率。為了估計P，採用最大似然估計，似然函數可以寫作

其中

表示實驗結果為i的次數。下面求似然函數的極值點，有

得到參數p的最大似然估計值為

可以看出二項分佈中每次事件發的概率p就等於做N次獨立重複隨機試驗中事件發生的概率。

如果我們做20次實驗，出現正面12次，反面8次

那麼根據最大似然估計得到參數值p為12/20 = 0.6。

2、最大後驗估計MAP

最大後驗估計與最大似然估計相似，不同點在於估計

的函數中允許加入一個先驗

，也就是説此時不是要求似然函數最大，而是要求由貝葉斯公式計算出的整個後驗概率最大，即

注意這裏P（X）與參數

無關，因此等價於要使分子最大。與最大似然估計相比，現在需要多加上一個先驗分佈概率的對數。在實際應用中，這個先驗可以用來描述人們已經知道或者接受的普遍規律。例如在扔硬幣的試驗中，每次拋出正面發生的概率應該服從一個概率分佈，這個概率在0.5處取得最大值，這個分佈就是先驗分佈。先驗分佈的參數我們稱為超參數(hyperparameter)即

同樣的道理，當上述後驗概率取得最大值時，我們就得到根據MAP估計出的參數值。給定觀測到的樣本數據，一個新的值

發生的概率是

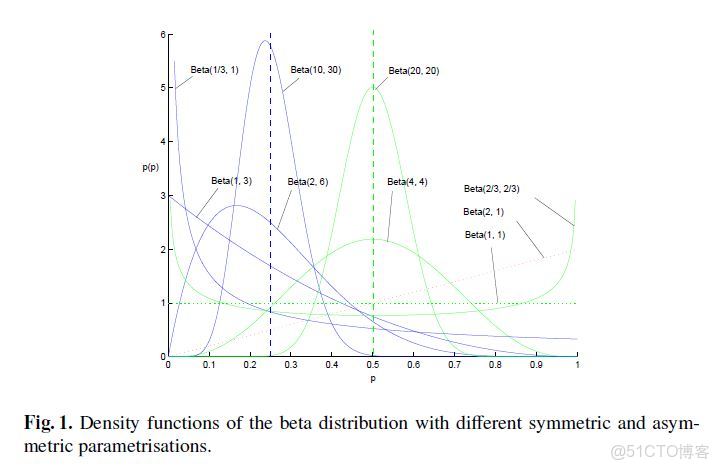
下面我們仍然以扔硬幣的例子來説明，我們期望先驗概率分佈在0.5處取得最大值，我們可以選用Beta分佈即

其中Beta函數展開是

當x為正整數時

Beta分佈的隨機變量範圍是[0,1],所以可以生成normalised probability values。下圖給出了不同參數情況下的Beta分佈的概率密度函數

我們取

,這樣先驗分佈在0.5處取得最大值，現在我們來求解MAP估計函數的極值點，同樣對p求導數我們有

得到參數p的的最大後驗估計值為

和最大似然估計的結果對比可以發現結果中多了

這樣的pseudo-counts,這就是先驗在起作用。並且超參數越大，為了改變先驗分佈傳遞的belief所需要的觀察值就越多，此時對應的Beta函數越聚集，緊縮在其最大值兩側。

如果我們做20次實驗，出現正面12次，反面8次，那麼

那麼根據MAP估計出來的參數p為16/28 = 0.571,小於最大似然估計得到的值0.6，這也顯示了“硬幣一般是兩面均勻的”這一先驗對參數估計的影響。

3 貝葉斯估計

貝葉斯估計是在MAP上做進一步拓展，此時不直接估計參數的值，而是允許參數服從一定概率分佈。回顧一下貝葉斯公式

現在不是要求後驗概率最大，這樣就需要求

,即觀察到的evidence的概率，由全概率公式展開可得

當新的數據被觀察到時，後驗概率可以自動隨之調整。但是通常這個全概率的求法是貝葉斯估計比較有技巧性的地方。

那麼如何用貝葉斯估計來做預測呢？如果我們想求一個新值

的概率，可以由

來計算。注意此時第二項因子在上的積分不再等於1，這就是和MLE及MAP很大的不同點。

我們仍然以扔硬幣的伯努利實驗為例來説明。和MAP中一樣，我們假設先驗分佈為Beta分佈，但是構造貝葉斯估計時，不是要求用後驗最大時的參數來近似作為參數值，而是求滿足Beta分佈的參數p的期望，有

注意這裏用到了公式

當T為二維的情形可以對Beta分佈來應用；T為多維的情形可以對狄利克雷分佈應用

根據結果可以知道，根據貝葉斯估計，參數p服從一個新的Beta分佈。回憶一下，我們為p選取的先驗分佈是Beta分佈，然後以p為參數的二項分佈用貝葉斯估計得到的後驗概率仍然服從Beta分佈，由此我們説二項分佈和Beta分佈是共軛分佈。在概率語言模型中，通常選取共軛分佈作為先驗，可以帶來計算上的方便性。最典型的就是LDA中每個文檔中詞的Topic分佈服從Multinomial分佈，其先驗選取共軛分佈即Dirichlet分佈；每個Topic下詞的分佈服從Multinomial分佈，其先驗也同樣選取共軛分佈即Dirichlet分佈。

根據Beta分佈的期望和方差計算公式，我們有

可以看出此時估計的p的期望和MLE ，MAP中得到的估計值都不同，此時如果仍然是做20次實驗，12次正面，8次反面，那麼我們根據貝葉斯估計得到的p滿足參數為12+5和8+5的Beta分佈，其均值和方差分別是17/30=0.567, 17*13/(31*30^2)=0.0079。可以看到此時求出的p的期望比MLE和MAP得到的估計值都小，更加接近0.5。

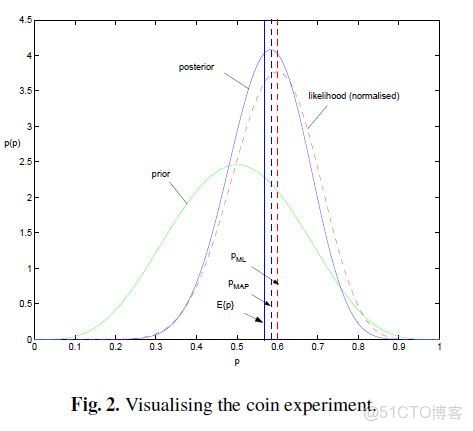
綜上所述我們可以可視化MLE,MAP和貝葉斯估計對參數的估計結果如下

個人理解是，從MLE到MAP再到貝葉斯估計，對參數的表示越來越精確，得到的參數估計結果也越來越接近0.5這個先驗概率，越來越能夠反映基於樣本的真實參數情況。

4.三者之間的區別

    首先我們可以看到,最大似然估計和最大後驗估計都是基於一個假設，即把待估計的參數π看做是一個固定的值，只是其取值未知。而最大似然是最簡單的形式，其假定參數雖然未知，但是是確定值，就是找到使得樣本對數似然分佈最大的參數。而最大後驗，只是優化函數為後驗概率形式，多了一個先驗概率項。 而貝葉斯估計和二者最大的不同在於，它假定參數是一個隨機的變量，不是確定值。在樣本分佈P(π|χ)上，π是有可能取從0到1的任意一個值的，只是取到的概率不同。而MAP和MLE只取了整個概率分佈P(π|χ)上的一個點，丟失了一些觀察到的數據χ給予的信息（這也就是經典統計學派和貝葉斯學派最大的分歧所在。）