---

本週為第二課的第三週內容，你會發現這周的題目很長，實際上，作為第二課的最後一週內容，這一週是對基礎部分的最後補充。
在整個第一課和第二課部分，我們會了解到最基本的全連接神經網絡的基本結構和一個完整的模型訓練，驗證的各個部分。
之後幾課就會進行更多的實踐和進階內容介紹，從“通用”走向“特化”。
總的來説這周的難度不高，但也有需要理解的內容，我仍會在相對較難理解的部分增加更多基礎和例子，以及最後的“人話版”總結。

本篇的內容關於多值預測與多分類，之前的內容裏我們一直只進行“是”或“不是”的二分類或者單值預測，通過本篇的瞭解後，便可以拓展到多分類和多值預測。

1. 神經網絡的輸出層

在之前的內容裏，我們基本默認神經網絡的輸出層只有一個神經元。
而要從單值預測到多值預測，從二分類拓展到多分類，最大的改變就是神經網絡輸出層的神經元數量。
現在，我們展開敍述一下神經網絡輸出層不同數量的神經元所帶來的影響。

1.1 輸出層為單個神經元

這是我們之前一直使用的結構，它的含義取決於你在做什麼任務：
如果是預測任務，我們便認為這個神經元的輸出是最終的預測值。
如果是分類任務，我們便把這個神經元經過sigmoid激活函數的輸出視為“是”的概率。
簡單展開一下：

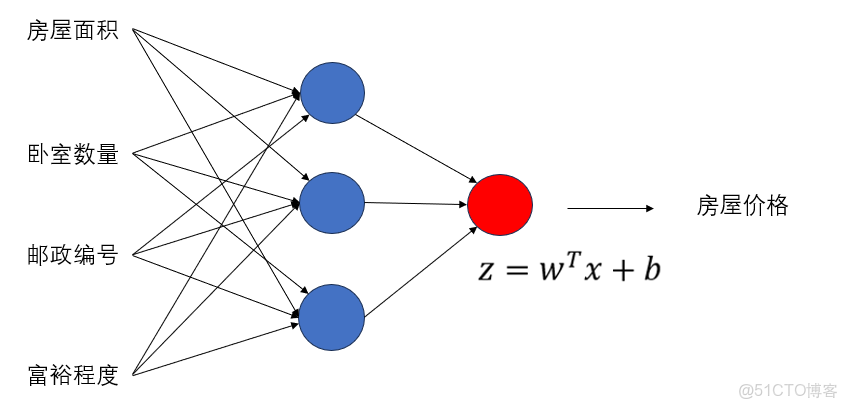
（1）迴歸任務

比如預測房價、預測温度這種“輸出一個具體數值”的任務：
在這種任務裏，我們的”答案“ 就是房價或者温度，因此，整個網絡就是在通過輸入擬合最終這個”答案“。
因此：

• 輸出層一個神經元
• 不加激活函數
• 輸出值直接就是模型的預測結果

就像這樣：

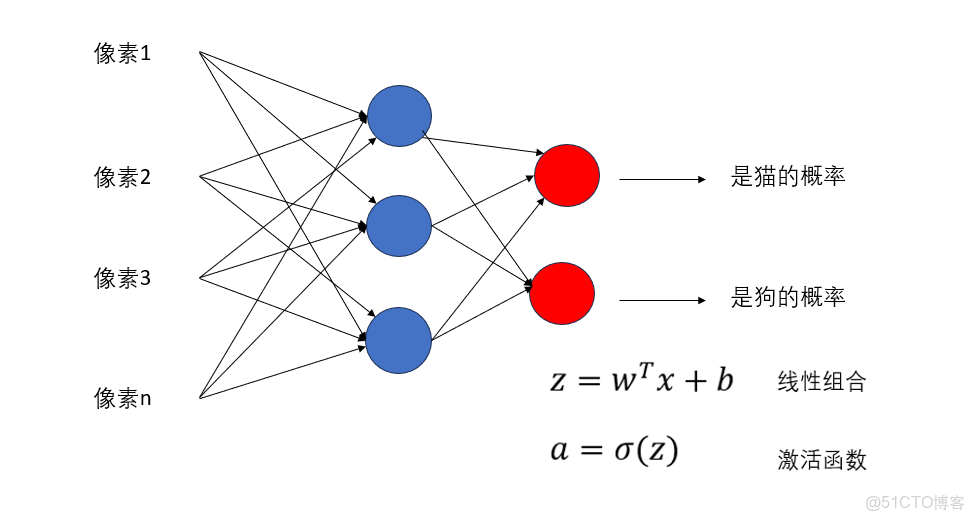
（2）二分類任務

就是我們一直在用的“貓狗分類”，
迴歸和分類在邏輯上是相通的，只看我們的處理方式。在這個例子裏，我們的“答案”就是”是不是貓“，不同於迴歸問題的具體數值，二分類的輸出是一個”是不是“即 ”0或1“的選擇。
因此：

• 輸出層一個神經元
• 最後接一個 sigmoid
• 輸出在 0~1 之間，通過決策閾值進行選擇，可以理解為“是”的概率
  這種結構我們已經非常熟悉了，我們之前所有分類例子都是這種方式。
  就像這樣：

1.2 輸出層為兩個神經元

當輸出層的神經元數量從 1 個變為 2 個時，模型的輸出形式就發生變化了：
它從“輸出一個值 / 一個概率”，變成了“輸出兩個值 / 兩個概率”。
這種結構在兩類場景下非常常見：
（1）預測兩個連續量的迴歸任務。
（2）二分類任務的另一種表達方式(實際上並不常用)
我們逐一展開。

（1）預測兩個連續量回歸任務

上面我們用温度和房價來舉例預測一個連續量的任務。
但在生活中，我們你也會遇到一些模型需要同時預測兩個值的情況，例如：

• 預測一個物體的 x 座標 和 y 座標
• 預測產品的 高度 和 寬度
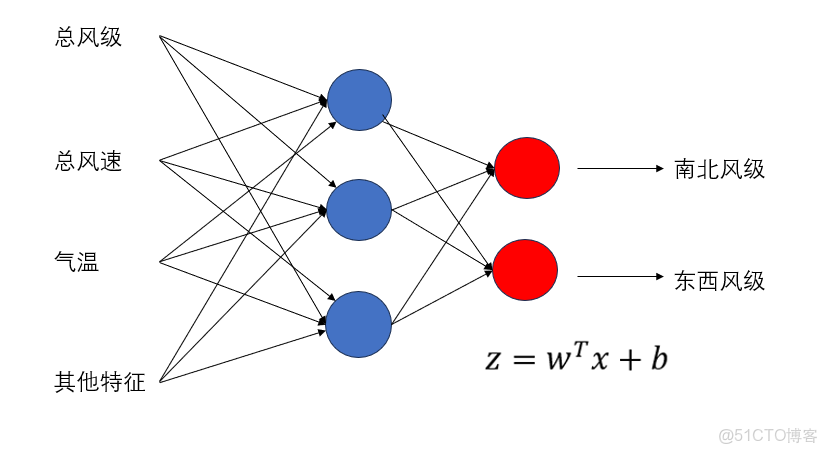
• 預測天氣中的 風的兩個分量（ 東西方向風和南北方向風）
  在這樣的任務要求中，需要預測的量變成了兩個，就像是我們原本的”答案“只有一個空要填，現在要填兩個。
  因此：
• 輸出層兩個神經元
• 依舊不加激活函數（保持數值範圍連續）
• 每個神經元輸出一個獨立的迴歸值，各自代表一項預測結果。
  模型最終的輸出是兩個具體數值，如：

\[[3.5,\ 1.2] \]

直觀的理解就是： 網絡要輸出兩個信息，所以自然需要兩個神經元各自負責一項。

就像這樣：

（2）二分類任務的另一種表達

我們已經非常習慣 “一個神經元 + sigmoid” 的二分類方式了。
但實際上，如果按照剛剛二值預測的迴歸邏輯，那其實二分類也應該使用兩個輸出層神經元來表示才對吧？
就像我們一直用的貓狗二分類，實際在邏輯上，我們不應該輸出”是貓的概率“和”是狗的概率“嗎？
為什麼我們能只用一個輸出層神經元來進行二分類，答案很簡單，相信不用我多解釋：
因為二分類是一個非黑即白，非此即彼的問題。
所以我們用下面這樣的邏輯來化簡了網絡結構：

\[是A的概率+決策閾值=是A的概率+是B的概率+取A,B中的大值 \]

因此，這其實只是二分類任務的另一種表達，且我們並不常用，形式如下：

• 輸出層兩個神經元
• 最後接 softmax
• softmax 輸出的是一個長度為 2 的概率分佈

\[ [P(\text{類1}),\ P(\text{類2})] \]

• 兩個概率加起來一定等於 1
  這裏要説明：softmax是針對多分類問題的激活函數，它和sigmoid的區別，為什麼適用，我們在下面馬上就會展開介紹。
• 就像這樣：



• 
  

1.3 輸出層為多個神經元

當輸出層的神經元數量從 2 個繼續擴展到更多個時，本質上意味着：
我們希望神經網絡一次性輸出更多的信息。
這種結構在迴歸和分類領域都非常常見，我們依舊像前面一樣分兩種情況展開。

（1）預測多個連續量的迴歸任務

上面的內容中，我們分別預測了一個值（房價）、兩個值（x,y 風向）。
而在很多實際任務中，“答案”往往不止兩個，有時候甚至要預測一整個向量。
例如：

• 一次預測物體的 位置 + 寬度 + 高度 + 朝向（共 4 個值）
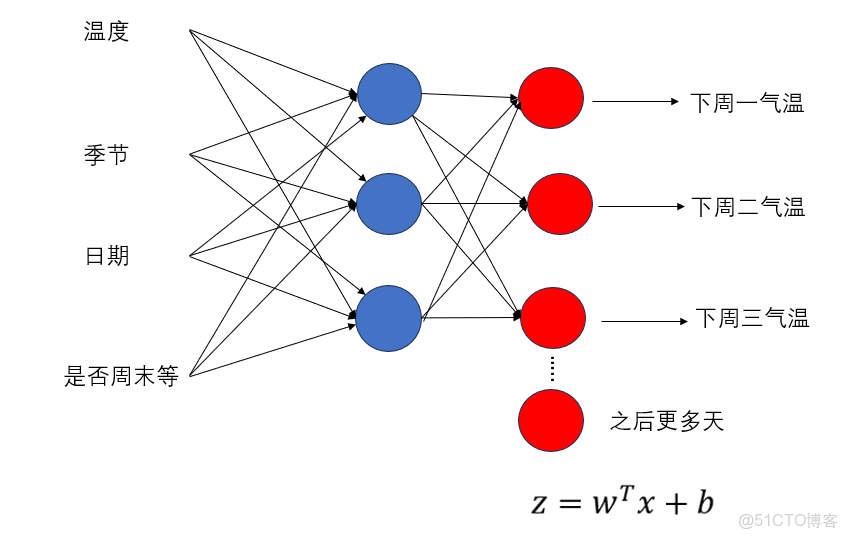
• 一次預測未來 多天的氣温序列（比如預測未來 7 天，每天一個温度，共 7 個輸出）
• 預測某個過程的 多個物理量（速度、加速度、角速度、角加速度……）
  這些任務都在告訴我們：
  需要輸出多少個數，輸出層就要給多少個神經元。
  因此：
• 輸出層有 n 個神經元
• 每個神經元負責預測一個獨立的連續值
• 輸出層一般 不加激活函數（保持迴歸問題需要的連續範圍）
  這樣，模型最終輸出的是一個 n 維向量，例如：

還是用答案打比方：原本答案只有一個空，現在有 n 個空，所以輸出層神經元自然跟着變多。

就像這樣：

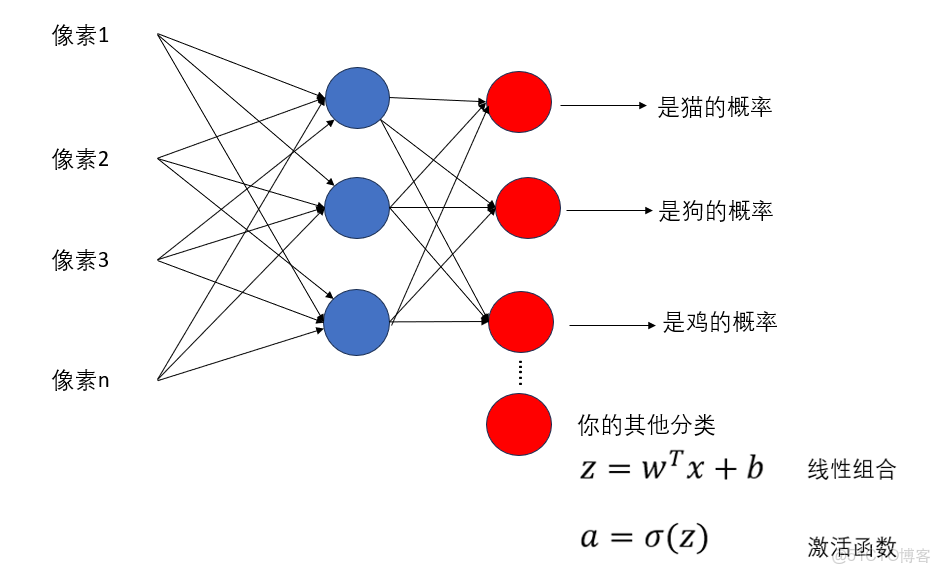
（2）多分類任務

前面我們説過：

• 二分類判斷的是 是不是（0 或 1）
• 多分類判斷的是 是哪一種（從多個類別中選 1）
  因此非常自然地：
  輸出層的神經元數量 = 類別數量
  例如：
• 手寫數字識別：10 種 → 輸出層 10 個神經元
• 動物識別：5 種 → 輸出層 5 個神經元
• 情感分析：3 種 → 輸出層 3 個神經元
  當類別多起來時，我們不能再用一個神經元得出一個概率了。
  所以它的輸出結構變為：
• 輸出層 n 個神經元
• 最後接 softmax 激活函數
• softmax 把 n 個輸出變成一個概率分佈

簡單來説：每個神經元都是一個“類別候選”，softmax 會讓它們“競爭”，誰分最高就是誰。

現在可能還不太清晰，別擔心，我們馬上就會詳細展開。

先來看一下網絡結構，就像這樣：

總之，輸出層有多少神經元，完全取決於你的任務希望模型給你多少信息。

2. 多分類的核心：softmax

在上面我們提到：
當輸出層神經元從 1 個擴展到多個時，分類任務往往使用 softmax 來得到一個“概率分佈”。
但為什麼我們之前一直用的 sigmoid 不行呢？
softmax 又到底“厲害”在哪裏？
這裏我們就來詳細展開：

2.1 sigmoid 為什麼不適用多分類問題？

我們第一次介紹sigmoid是在這裏：激活函數和反向傳播 通過之前的學習內容：我們可以簡單地總結：
sigmoid 的本質，就是把一個數壓到 0~1，用來表示“是”的概率。
這種映射非常適合二分類，因為二分類的問題就是：

是 / 不是
1 / 0
貓 / 不是貓

可到了多分類問題裏，它就會出現一些問題，我們來展開説明：

（1）sigmoid的分類邏輯

現在，假如我們要做 3 類分類：貓 / 狗 / 老虎。
如果輸出層有三個神經元，每個都接 sigmoid，那麼可能出現：

類別	sigmoid 輸出
貓	0.9
狗	0.8
老虎	0.85

這些概率 加起來不是 1，並且三個看起來都“很像”，但我們的問題本質是 —— 只能選其中一個！
sigmoid 的輸出互不影響，彼此獨立，就像問模型三次：

• 像貓嗎？
• 像狗嗎？
• 像老虎嗎？
  模型每次都可以説“很像”。
  這顯然不符合“選一個類別”的邏輯。
  你可能會説：那我選最大的可能，也就是輸出最大的那個不就行了嗎？
  這麼做看起來是一個解決方案，但它的核心問題是：沒有考慮到傳播，這會對擬合產生極大影響。

（2）為什麼不能只“選最大”？

我們就上面這個問題繼續展開：
比如真實標籤是“貓”，也就是説正確答案是：

• 貓：1
• 狗：0
• 老虎：0
  但因為三個 sigmoid 之間互不影響，模型可以學到一種非常奇怪但“不會被懲罰”的策略：
• 貓：0.99（正確，因為要接近 1）
• 狗：0.95（雖然應該接近 0，但 sigmoid 的 loss 不會讓它“被壓下很多”）
• 老虎：0.97（同上）
  只要“貓”這一類夠高，它就能被認為預測正確。
  換句話説：sigmoid 的多分類本質上是 3 個互不相關的二分類任務，它無法學到“如果是貓，那就不應該是狗或老虎”。
  這是為什麼？我們再來複習一下二分類的損失函數，它第一次出現在這裏：損失函數

（3）從損失函數看sigmoid

sigmoid 的損失函數（二分類交叉熵損失，Binary Cross-Entropy）如下：
對於單個神經元輸出 \(\hat{y}\) 和真實標籤 \(y \in {0,1}\)：

這條公式告訴我們：

• 當 \(y=1\) 時，loss 只關注讓 \(\hat{y}\)
• 當 \(y=0\) 時，loss 只關注讓 \(\hat{y}\)

現在回到三分類的例子：貓 / 狗 / 老虎
我們計算它的一次傳播如下：

類別	真實標籤 \(y\)	模型輸出 \(\hat{y}\)	Loss 公式	Loss 值
貓	1	0.99	\(-\log 0.99\)	\(\approx 0.01\)
狗	0	0.95	\(-\log (1-0.95)\)	\(\approx 3.0\)
老虎	0	0.97	\(-\log (1-0.97)\)	\(\approx 3.0\)

看上去似乎其他類別會被壓低，為什麼會出現“它們也很像”這種情況呢？
關鍵在於 梯度的傳播和訓練目標：

• 每個 sigmoid 輸出對應一個 獨立的二分類任務
• 當使用 mini-batch 或者權重初始化不理想時，梯度更新仍可能非常弱，讓梯度消失。
• 模型可以通過調整權重讓 貓 輸出極大，同時讓 狗/老虎 也維持相對高值，只要最終“貓”的輸出比閾值高，整體預測還是正確的。sigmoid 沒有全局約束去強制其他輸出必須降低。

總的來説：sigmoid它沒有“互斥性“的邏輯，在二分類裏，它可以只針對正類不斷強化，因為不是正類自然就是負類。
而現在的多分類裏，它不知道“只有一個類別應該成立”，”懲罰力度”不夠大，對錯誤類別的拳不夠快，不夠狠！
這就是它的不適用性的核心重點，再直白點：它很好，只是現在在這方面有比它更好的。
不過這也並不絕對，在一些多標籤多分類問題裏，sigmoid反而更適用，我們遇到再説。

2.2 softmax 如何適應多分類問題？

接下來，我們的主角是 softmax。

如果説 sigmoid 是“我像不像貓？”，
那麼 softmax 更像是：“把所有類別排排隊，看誰最像”，也就是説，它會讓各個類別互相 競爭，最後給出一個 概率分佈。

它的數學形式如下：

\[P_i = \frac{e^{z^{(i)}}}{\sum_j e^{z{[j]}}} \]

並不複雜，我們一一展開這個公式的組成：

(1) 把輸出轉為正數並凸顯最優類別

我們知道，網絡輸出的 \(z^{(i)}\) 可能是負數、零或正數，直接當作概率不行。
所以，softmax 先用指數函數 \(e^{z^{(i)}}\) 轉換：
1. 保證所有值為正
2. 放大原本相近的差距，使“最優類別”更明顯。

舉個實例：

這樣，第一個類別概率最高 → 最可能被選中
同時，指數化差別被放大→ 其他類別自動壓低更多 → 避免像 sigmoid 那樣“多個類別都很高”。
現在來看下一步：

（2）把指數值歸一化成概率

直白的説，就是把數值轉變成這個數佔所有數和的比例。
繼續上面的例子：

這樣下來：

1. 所有 \(P_i\)
2. 所有 \(P_i\)

這正好符合單標籤多分類問題的要求：“輸出一個概率分佈，所有類別概率加起來為 1。”

補充一點：什麼叫單標籤多分類，什麼叫多標籤多分類？

1. 單標籤多分類：每個樣本只對應一個標籤：一張圖裏只有貓或狗。
2. 多標籤多分類：每個樣本可以對應多個標籤：一張圖裏可以同時有貓和狗。

（3）總結 softmax 的優勢

• 互斥性：輸出自然體現“只能選一個類別”的邏輯
• 概率分佈：所有輸出加和為 1，方便解釋和比較
• 指數放大：最可能的類別更明顯，更易學習
  這便是softmax 適合多分類的原因所在。

2.3 softmax的損失函數

在二分類裏，我們用 Binary Cross-Entropy（BCE） 來衡量預測概率和真實標籤的差距。
在多分類裏，softmax 對應的損失函數叫 Categorical Cross-Entropy（多分類交叉熵）。
它如何和 softmax 配合？我們來看看。

（1）損失函數公式

假設樣本真實類別是 \(y\)，模型預測概率是 \(P_i\)，那麼損失函數為：

注意，這裏假設用一種叫獨熱編碼的技術表示類別，不會因用1，2，3表示類別而出現數值差別，我們後面就會了解到。
現在解釋一下：

• \(y_i\)
• \(y_i\)
• 損失只關注正確類別對應的概率 \(P_\text{正確類別}\)
• 如果正確類別的概率越高，\(\log P_\text{正確類別}\) 越接近 0，損失越小
  來看一個實例。

（2）舉例説明

假設一個三分類問題（貓 / 狗 / 老虎），真實類別是“貓”，模型 softmax 輸出概率為：

• 正確類別貓 → \(y = [1,0,0]\)
• 損失計算：

再來看一個不理想的情況：

• 損失：

可以看到：正確類別概率越高，損失越小；概率低，損失變大 → 模型會被強烈“懲罰”，迫使它把正確類別概率提高。

這樣，由於 softmax 的互斥性，提升正確類別概率的同時，其他類別概率會被壓低，反向傳播時梯度明確，模型容易學習，就避免 sigmoid 多分類中“多個類別都高”問題。

3. ”人話版“ 總結

概念	原理	比喻
單輸出神經元（迴歸任務）	輸出一個連續數值，直接作為預測結果，不加激活函數	就像填一張表格的一個空，直接寫結果
單輸出神經元（二分類任務）	輸出一個概率（sigmoid），表示“是/不是”的可能性	問模型：“這是不是貓？” → 得到 0~1 的答案
兩個輸出神經元（迴歸任務）	輸出兩個獨立連續數值，每個神經元負責一項預測	原本填一個空，現在要填兩個空（比如預測 x, y 座標）
兩個輸出神經元（二分類任務）	輸出兩個概率（softmax），表示兩類的概率和為1	給貓和狗各發一張票，看看誰票多 → 貓或狗獲勝
多輸出神經元（迴歸任務）	輸出 n 個連續數值，每個神經元預測一個量	一次預測多個空，例如物體的位置、寬度、高度…
多輸出神經元（多分類任務）	輸出 n 個概率（softmax），形成概率分佈，和為 1	所有候選類別排隊投票，票多的就是預測類別
sigmoid 多分類問題	每個輸出獨立，無法體現“互斥性”，可能出現多個高概率類別	三個人獨立問：“像貓嗎？”“像狗嗎？”“像老虎嗎？” → 每個人都説“很像”，模型很困惑
softmax 多分類問題	輸出互斥概率，提升正確類別概率時自動壓低其他類別概率	總票數一定，有人票多，其他人自然票少 → 模型更聰明、更有方向性
損失函數	二分類用 BCE，多分類用 Categorical Cross-Entropy	損失就是“罰款”：預測越錯 → 罰得越重 → 模型被迫改正