1. 線性代數是什麼？

線性代數是數學的一個重要分支，主要研究向量、矩陣、線性方程組和線性變換等概念。如果把深度學習比作一棟高樓，那麼線性代數就是這棟高樓的"鋼筋骨架"——它雖然不直接可見，卻支撐着整個建築的結構穩定性。

1.1 基本數學對象

在深度學習中，數據通常以以下幾種形式表示：

• 標量(Scalar)：單個數字，比如温度值25℃或者商品價格99.5元
• 向量(Vector)：一維數組，比如一個學生的各科成績 [數學90, 英語85, 物理88]
• 矩陣(Matrix)：二維表格，比如全班學生的成績單：

| 數學 | 英語 | 物理 |
張三 |  90  |  85  |  88  |
李四 |  78  |  92  |  85  |

• 張量(Tensor)：多維數組，這是深度學習中最常用的數據結構，比如多個班級多個科目的成績表（3維)

1.2 為什麼線性代數對深度學習如此重要？

深度學習本質上是大規模的數據變換和特徵提取，而這些操作幾乎都是通過矩陣運算完成的。舉個例子，在神經網絡中，每一層都可以看作是一個線性變換（加上非線性激活函數）：輸入數據與權重矩陣相乘，加上偏置向量，得到輸出結果。這種矩陣運算可以高度並行化，這正是GPU能夠加速深度學習訓練的原因。

2. 核心概念與運算詳解

2.1 矩陣運算及其幾何意義

矩陣加法/減法

對應位置元素相加或相減，就像合併兩份成績單後計算總分或差異。從幾何角度看，矩陣加法相當於向量的平移變換。

矩陣乘法：深度學習的核心運算

矩陣乘法是深度學習中最常見且最重要的運算。例如，在一個簡單的神經網絡層中：

輸出 = 輸入 × 權重矩陣 + 偏置

或者用數學公式表示：y = Wx + b

其中W是權重矩陣，x是輸入向量，b是偏置向量。這種矩陣乘法允許我們同時處理大量數據，極大提高了計算效率。

矩陣轉置

將矩陣的行列互換，類似於把橫着的表格豎過來看。在深度學習中，轉置常用於確保矩陣維度匹配，以便進行乘法運算。

表1：基本矩陣運算及其在深度學習中的應用

2.2 行列式：衡量線性變換的"縮放因子"

行列式是方陣的一個標量值，可以判斷矩陣是否可逆。從幾何角度看，行列式的絕對值表示線性變換後面積或體積的縮放比例，符號表示方向是否改變。

• 行列式為0：表示矩陣不可逆，變換後維度降低（如從平面壓縮到直線）
• 行列式為1：保持面積/體積不變的變換（如旋轉）

2.3 範數：度量向量"大小"的尺子

範數用於衡量向量的"大小"或"長度"，在深度學習中常用於正則化，防止模型過擬合：

L1 範數（曼哈頓範數）

• 定義：向量所有分量絕對值的和。
• 公式：
• 例子：向量 [3, 4] 的 L1 範數 = |3| + |4| = 7。
• 幾何意義：在二維平面上，像是從點(0,0)走到點(3,4)的“曼哈頓距離”（只能沿網格走），總路程是7。
• 主要用途：在機器學習中用於L1正則化（Lasso正則化），它可以產生稀疏模型，即讓不重要的特徵權重變為0，從而實現特徵選擇。

L2 範數（歐幾里得範數）

• 定義：向量各分量平方和再開根號。這是最直觀的“長度”概念。
• 公式：
• 例子：向量 [3, 4] 的 L2 範數 = 。
• 幾何意義：就是空間中兩點之間的直線距離。
• 主要用途：最常用的範數。在機器學習中用於L2正則化（嶺迴歸），它通過懲罰較大的權重來防止過擬合，但通常不會將權重恰好降為0。

L∞ 範數（最大範數）

• 定義：向量所有分量絕對值的最大值。
• 公式：
• 例子：向量 [3, 4] 的 L∞ 範數 = max(|3|, |4|) = 4。
• 幾何意義：衡量的是向量在任意座標軸方向上的最大變化量。
• 主要用途：在某些工程和數學領域，當系統的性能由最大誤差決定時，會使用此範數。

3. 線性方程組：深度學習中的"應用題"

線性方程組的一般形式是 Ax = b，其中：

• A是係數矩陣（如各科成績的權重）
• x是未知數向量（如各科得分）
• b是結果向量（如總分）

3.1 解的存在性與唯一性

根據線性代數理論，方程組解的情況有以下幾種：

1. 有唯一解：當A是滿秩方陣時，存在唯一解 x = A⁻¹b
2. 有無窮多解：當方程數少於未知數時（欠定系統）
3. 無解：當方程之間存在矛盾時（超定系統）

在深度學習中，我們經常遇到超定系統（方程數多於未知數），這時我們尋找最小二乘解，即最小化 ||Ax - b||²，這正好是線性迴歸和神經網絡的基礎。

3.2 實際應用案例：房價預測

假設我們想根據房屋面積、卧室數量和地理位置預測房價。我們可以建立如下線性模型：

房價 = w₁ × 面積 + w₂ × 卧室數 + w₃ × 位置評分 + b

收集多組房屋數據後，我們可以構建線性方程組，並用矩陣形式表示為 y = Xw，其中X是特徵矩陣，w是權重向量，y是房價向量。

4. 線性變換：深度學習的"靈魂"

4.1 什麼是線性變換？

數學定義：
對於任意向量 , 和標量 ，變換

1. 可加性：
2. 齊次性：

簡單例子：
假設有一個線性變換 ，其對應的矩陣為：

對向量 進行變換：

這就是一個簡單的縮放變換：x方向放大2倍，y方向放大3倍。

在深度學習中，神經網絡的每一層都在進行這樣的線性變換：輸出 = 權重矩陣 · 輸入 + 偏置。

4.2 特徵值與特徵向量：揭示變換的本質

數學定義：
對於矩陣 ，如果存在非零向量 和標量 ，使得：

則稱 是 的特徵向量，

簡單例子：
考慮矩陣
求解特徵值：

解得特徵值：,

對 ，求特徵向量：

解得

對 ，求特徵向量：

解得

在深度學習中，特徵值分析有助於理解模型的穩定性和優化過程。例如，梯度下降法的收斂速度與Hessian矩陣的特徵值分佈密切相關。

4.3 在深度學習中的關鍵應用

優化過程中的重要性：
梯度下降法的收斂速度確實與Hessian矩陣的特徵值分佈密切相關。損失函數 在點 的Hessian矩陣 包含二階導數信息：

收斂性分析：
學習率 的選擇與最大特徵值 相關，需要滿足：

才能保證梯度下降法的收斂性。

條件數的影響：
條件數

• ：容易優化（各方向曲率相似）
• ：難以優化（需要謹慎選擇學習率）

這種特徵值分析幫助我們理解為什麼某些神經網絡結構更難訓練，也為改進優化算法提供了理論基礎。

通過理解線性變換和特徵分析，我們能夠更深入地洞察深度學習模型的行為和性能特徵，為模型設計和優化提供理論指導。

5. 實際案例：用Python實現線性代數運算

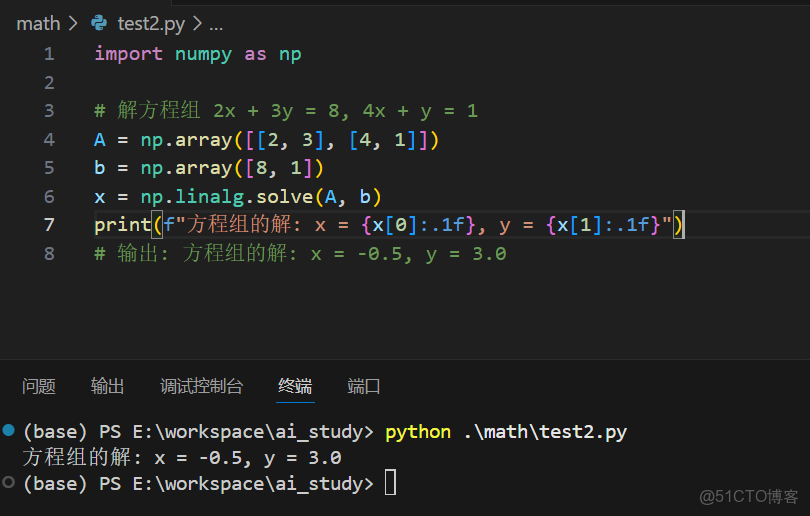
5.1 解線性方程組

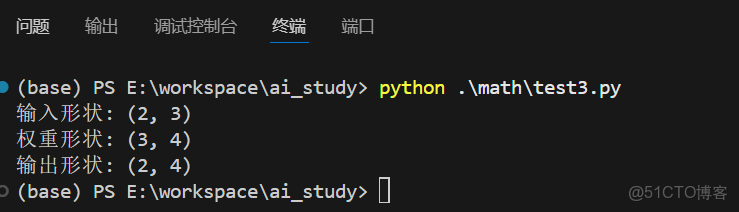
5.2 矩陣乘法模擬神經網絡層

# 模擬一個簡單的神經網絡層
input_size = 3
hidden_size = 4
batch_size = 2
# 隨機生成輸入數據和權重矩陣
X = np.random.randn(batch_size, input_size)  # 輸入矩陣
W = np.random.randn(input_size, hidden_size)  # 權重矩陣
b = np.random.randn(hidden_size)  # 偏置向量
# 前向傳播計算
Z = np.dot(X, W) + b  # 線性變換
print("輸入形狀:", X.shape)
print("權重形狀:", W.shape)
print("輸出形狀:", Z.shape)

運行結果:

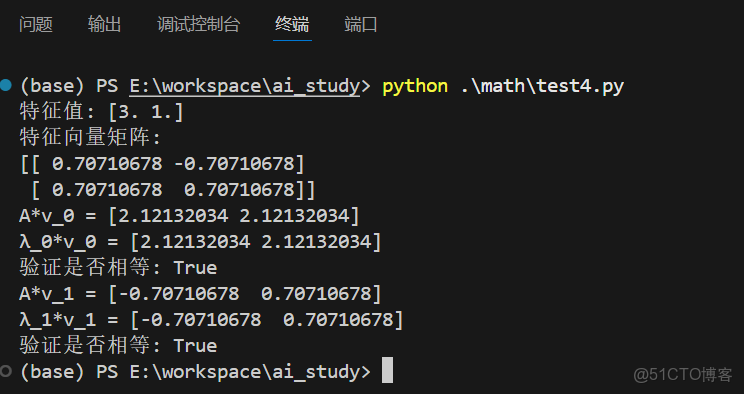
5.3 特徵值分解

# 對稱矩陣的特徵值分解
A = np.array([[2, 1], [1, 2]])
eigenvalues, eigenvectors = np.linalg.eig(A)
print("特徵值:", eigenvalues)
print("特徵向量矩陣:")
print(eigenvectors)
# 驗證特徵值定義: A*v = λ*v
for i in range(len(eigenvalues)):
v = eigenvectors[:, i]
λ = eigenvalues[i]
print(f"A*v_{i} = {np.dot(A, v)}")
print(f"λ_{i}*v_{i} = {λ*v}")
print("驗證是否相等:", np.allclose(np.dot(A, v), λ*v))

運行結果:

6. 線性代數在深度學習中的具體應用

6.1 卷積神經網絡(CNN)中的卷積運算

卷積操作本質上是矩陣的局部乘法。在圖像處理中，卷積核（一個小矩陣）在輸入圖像上滑動，進行局部矩陣乘法，提取特徵如邊緣、紋理等。

6.2 自注意力機制(Self-Attention)

Transformer模型中的自注意力機制核心是矩陣乘法：

Attention(Q, K, V) = softmax(QKᵀ/√d_k)V

其中Q(查詢)、K(鍵)、V(值)都是通過輸入向量與權重矩陣相乘得到的。這種機制允許模型關注輸入中不同部分的重要性。

6.3 主成分分析(PCA)用於降維

PCA通過特徵值分解尋找數據中方差最大的方向，用於高維數據可視化、去噪和特徵提取：

1. 計算數據協方差矩陣
2. 特徵值分解找到主成分
3. 投影到主成分空間實現降維

7. 總結

線性代數是深度學習的基礎語言和核心工具。從簡單的矩陣乘法到複雜的特徵值分解，線性代數為理解和實現深度學習模型提供了必要的數學框架。

通過本文的介紹，希望你能認識到線性代數不是一堆枯燥的公式，而是理解數據變換和特徵提取的強大工具。掌握線性代數，不僅能幫助你更深入理解深度學習原理，還能為學習更高級的機器學習算法打下堅實基礎。