leetcode 28 找出字符串中第一個匹配項的下標
# 該解答很簡單,大家閲讀一遍就會明白
class Solution(object):
def strStr(self, haystack, needle):
"""
:type haystack: str
:type needle: str
:rtype: int
"""
if not needle or not haystack: # 任一為空字符,必然沒結果
return -1
else:
n_start = needle[0]
length = len(needle)
min_index = 100000 # 題目裏規定≤10^4
for i in range(len(haystack)):
if haystack[i] == n_start and haystack[i:i+length] == needle: #首一樣再判斷
min_index = min(i,min_index)
else:
continue
if min_index != 100000:
return min_index
else:
return -1補充——如何計算時間、空間複雜度
時間複雜度
時間複雜度(Time Complexity)用於衡量算法執行所需時間相對於輸入規模的增長情況,通常用大O符號。
A 分析步驟
①確定基本操作: 找出最內層、執行次數最多的操作。
②統計基本操作的執行次數: 隨着輸入規模 n 的變化,操作執行了多少次。
③只保留最高階項,常數係數忽略,得出時間複雜度。
B 常見時間複雜度
|
時間複雜度
|
名稱
|
示例
|
|
O(1)
|
常數時間
|
訪問數組元素
|
|
O(log n)
|
對數時間
|
二分查找
|
|
O(n)
|
線性時間
|
遍歷數組, 乘法(字符串重複),比較
|
|
O(n log n)
|
線性對數時間
|
快速排序、歸併排序
|
|
O(n²)
|
二次時間
|
嵌套雙重循環,例如冒泡排序
|
|
O(2^n)
|
指數時間
|
遞歸解決子集、斐波那契數列等問題
|
|
O(n!)
|
階乘時間
|
全排列問題,如旅行商問題
|
C 舉例分析
# example 1
def sum_array(arr):
total = 0
for x in arr:
total += x
return total
# 基本操作(最內層):total += x
# 執行次數(直接讓規模為n):for x in arr每次循環執行一次加和操作, 總計會執行 n 次
# 時間複雜度:O(n)
# example 2
def bubble_sort(arr):
n = len(arr)
for i in range(n): # 外層循環:控制比較的輪數
for j in range(n - i - 1): # 內層循環:每輪比較相鄰元素
if arr[j] > arr[j+1]:
arr[j], arr[j+1] = arr[j+1], arr[j]
# 嵌套循環,兩層 for
# 執行次數: 外層for,執行了 n 次(i 從 0 到 n-1); 內層循環, 第 1 次外循環(i = 0):j 運行 0 ~ n-2,共執行 n-1 次,第 2 次外循環(i = 1):j 運行 0 ~ n-3,共執行 n-2 次,第 3 次外循環(i = 2):執行 n-3 次...
# 第 n-1 次外循環(i = n-1):執行 0 次
# 所以,總共的比較次數是——規模為n,加和內層循環次數,即(n−1)+(n−2)+(n−3)+⋯+1+0
# 時間複雜度:O(n(n-1)/2) 等價於 O(n^2)空間複雜度
A 分析步驟
①確定算法中使用的額外變量或數據結構
②表達成關於輸入規模 n 的函數
③忽略常數,保留最高階項
B 常見空間複雜度
|
空間複雜度
|
示例
|
|
O(1)
|
原地交換,使用常數個變量
|
|
O(n)
|
需要一個大小為 n 的數組
|
|
O(n²)
|
n × n 的二維矩陣
|
C 舉例分析
# example 1
def find_max(arr):
max_val = arr[0]
for x in arr:
if x > max_val:
max_val = x
return max_val
# 分析:只用了常數個變量:max_val、x。空間複雜度:O(1)
# example 2
def copy_array(arr):
new_arr = arr[:]
return new_arr
# 分析:“:” 表示不指定起始和結束位置,默認從頭到尾。即複製了一個大小為 n 的數組,空間複雜度:O(n)D 一些技巧
遞歸函數需要考慮遞歸棧的空間;
多重嵌套循環 → 時間複雜度通常是 O(n²)、O(n³)
申請了新數組、新列表 →會 影響空間複雜度
leetcode 459 重複的子字符串
# 我感覺這道題蠻難的,一起來學習下吧,順便掌握幾種思路寫法
方1:字符串拼接技巧法, 時間複雜度O(N)(遍歷字符串)
思想:
如果一個字符串s是由子串重複構成的,那麼將該字符串拼接一遍自己s+s,中間去掉頭尾一部分(s+s)[1:-1],它的原始字符串一定會在其中出現。【有人肯定會問,為啥?這樣,你寫個s = abc,然後按照這個思想推理一邊,你會發現abc not in "bcab" 裏】
# 原始字符串
s = a b a b
# 拼接後
s + s = a b a b a b a b
# 去掉首尾元素
(s + s)[1:-1] = b a b a b a
s in "b a b a b a"--> Trueclass Solution(object):
def repeatedSubstringPattern(self, s):
"""
:type s: str
:rtype: bool
"""
s_new = s + s
s_new_part = s_new[1:-1]
if s in s_new_part:
return True
else:
return False方2:暴力法(枚舉子串長度)
思想:
枚舉子串的長度L ,從 1 到 n//2 (子串最長的長度就是整體的一半);接着字符串長度能被 L整除,檢查整個字符串是否是這個子串重複的結果。
class Solution(object):
def repeatedSubstringPattern(self, s):
"""
:type s: str
:rtype: bool
"""
# 暴力法
n = len(s)
for L in range(1, n // 2 + 1):
if n % L == 0:
if s[:L] * (n // L) == s: # 子串*重複次數為字符串本身
return True
return False時間複雜度分析:
外層循環:子串長度枚舉,最多執行 n/2 次,複雜度O(n)
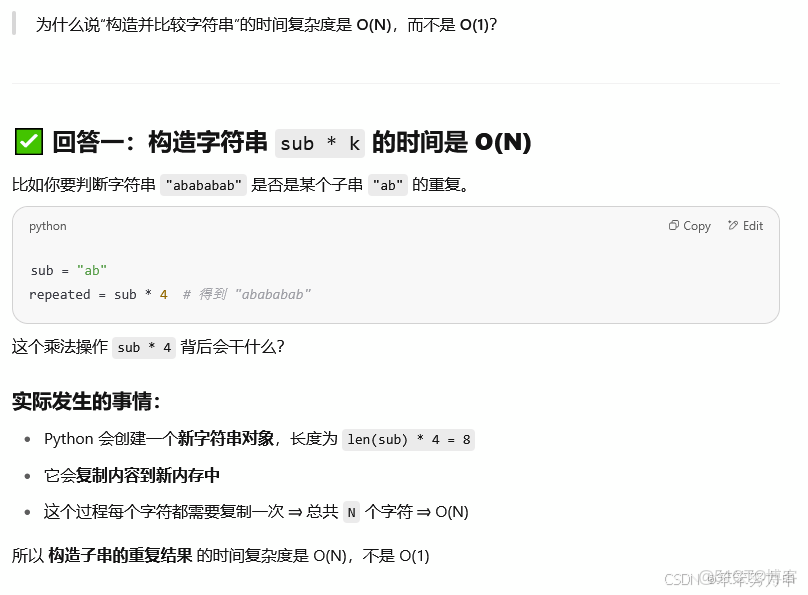
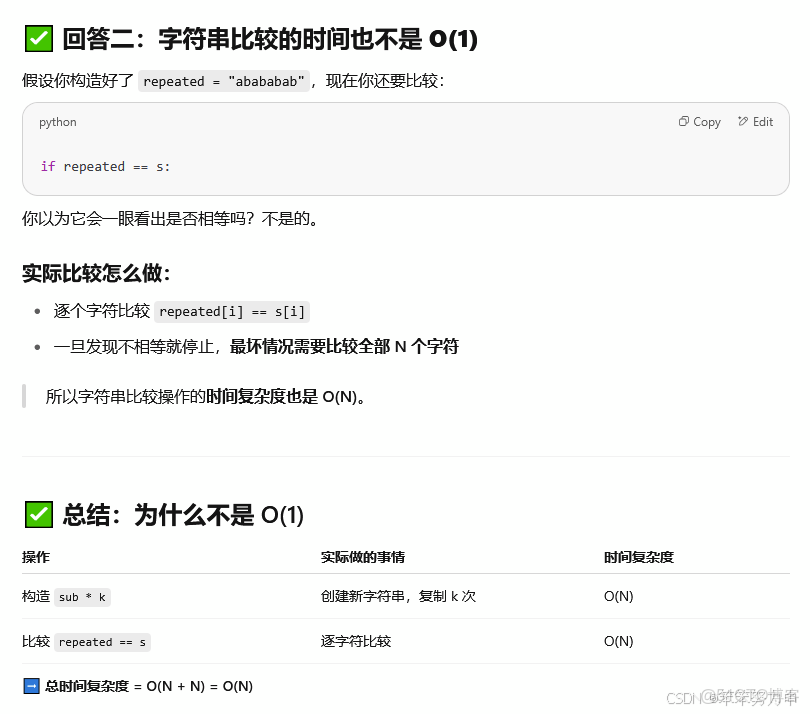
內層操作:重複構造 + 比較,最多進行n次(為什麼呢?第一遍壓根沒想通,不應該是O(1)嗎?且看如下分析)
總複雜度:我們最多執行O(n)次子串長度枚舉,每次都可能執行一個O(n)的構造 + 比較,故時間複雜度是O(n^2)
方3:KMP 前綴表
知識總結——關於KMP(Knuth-Morris-Pratt)前綴函數(也叫 next 數組)
什麼是【前綴】和【後綴】?——前綴是順序枚舉並遞增元素個數,不包含字符串本身;後綴反之
"ababc" 的前綴有:"a", "ab", "aba", "abab"
後綴有:"c", "bc", "abc", "babc"
什麼是 next 數組?
next[i] 表示:字符串前 i+1 個字符裏,前綴和後綴能匹配的最長長度(即找的是:前綴 == 後綴 的最長長度(不能包括整個字符串本身))。
舉個例子:s = "abab"(把每個next[i]寫出來)
|
i
|
子串 s[0:i]
|
最長前後綴
|
長度(next[i])
|
|
0
|
a
|
-
|
0
|
|
1
|
ab
|
無
|
0
|
|
2
|
aba
|
a
|
1
|
|
3
|
abab
|
ab
|
2
|