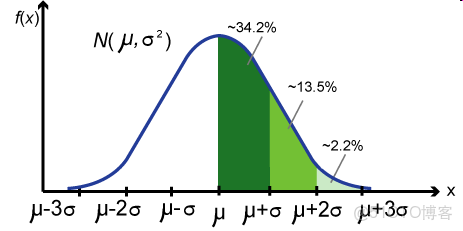
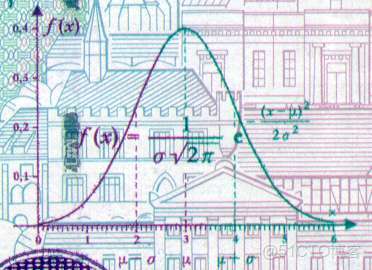正態分佈

 

神説，要有正態分佈，就有了正態分佈。 神看正態分佈是好的，就讓隨機誤差服從了正態分佈。 創世紀—數理統計

1. 正態分佈，熟悉的陌生人

學過基礎統計學的同學大都對正態分佈非常熟悉。這個鐘形的分佈曲線不但形狀優雅，它對應的密度函數寫成數學表達式

f(x)=1 2π− − √ σe −(x−μ) 2 2σ2  

也非常具有數學的美感。其標準化後的概率密度函數

f(x)=1 2π− − √ e −x 2 2  

更加的簡潔漂亮，兩個最重要的數學常量 π 、e 

 

正態分佈曲線

正態分佈又通常被稱為高斯分佈，在科學領域，冠名權那是一個很高的榮譽。2002年以前去過德國的兄弟們還會發現，德國1991年至2001年間發行的的一款10馬克的紙幣上印着高斯(Carl Friedrich Gauss, 1777-1855)的頭像和正態密度曲線，而1977年東德發行的20馬克的可流通紀念鋼鏰上，也印着正態分佈曲線和高斯的名字。正態分佈被冠名高斯分佈，我們也容易認為是高斯發現了正態分佈，其實不然，不過高斯對於正態分佈的歷史地位的確立是起到了決定性的作用。

   

德國馬克和紀念幣上的高斯頭像和正態分佈曲線

正態曲線雖然看上去很美，卻不是一拍腦袋就能想到的。我們在本科學習數理統計的時候，課本一上來介紹正態分佈就給出分佈密度函數，卻從來不説明這個密度函數是通過什麼原理推導出來的。所以我一直搞不明白數學家當年是怎麼找到這個概率分佈曲線的，又是怎麼發現隨機誤差服從這個奇妙的分佈的。我們在實踐中大量的使用正態分佈，卻對這個分佈的來龍去脈知之甚少，正態分佈真是讓人感覺既熟悉又陌生。直到我讀研究生的時候，我的導師給我介紹了陳希儒院士的《數理統計學簡史》這本書，看了之後才瞭解了正態分佈曲線從發現到被人們重視進而廣泛應用，也是經過了幾百年的歷史。

正態分佈的這段歷史是很精彩的，我們通過講一系列的故事來揭開她的神秘面紗。

 

2. 邂逅，正態曲線的首次發現

第一個故事和概率論的發展密切相關，主角是棣莫弗(Abraham de Moivre, 1667-1754) 和拉普拉斯 (Pierre-Simon Laplace 1749-1827)。拉普拉斯是個大科學家，被稱為法國的牛頓；棣莫弗名氣可能不算很大，不過大家應該都應該很熟悉這個名字，因為我們在高中數學學複數的時候都學過棣莫弗公式

(cosθ+isinθ) n =cos(nθ)+isin(nθ). 

而棣莫弗所寫的《機遇論》（The doctrine of chances）是概率論發展歷史中很重要的一本書。牛頓對棣莫弗十分欣賞,遇到學生向他請教概率方面的問題時，他就説：“這樣的問題應該去找棣莫弗，他對這些問題的研究比我深入得多。”

 

棣莫弗和拉普拉斯

古典概率論發源於賭博，惠更斯(Christiaan Huygens, 1629-1695)、帕斯卡(Blaise Pascal, 1623-1662)、費馬(Pierre de Fermat, 1601-1665)、雅可比·貝努利(Jacob Bernoulli, 1654-1705)都是古典概率的奠基人，他們那會研究的概率問題大都來自賭桌上，最早的概率論問題是賭徒梅累在1654年向帕斯卡提出的如何分賭金的問題。統計學中的總體均值之所以被稱為期望 (Expectation), 就是源自惠更斯、帕斯卡這些人研究平均情況下一個賭徒在賭桌上可以期望自己贏得多少錢。

第一位劍客就是卡爾.皮爾遜，手中的寶劍就是χ 2  分佈。 χ 2    分佈這把寶劍最早的鍛造者其實是物理學家麥克斯韋，他在推導空氣分子的運動速度的分佈的時候，發現分子速度在三個座標軸上的分量是正態分佈，而分子運動速度的平方v 2    符合自由度為3 的χ 2  分佈。麥克斯韋雖然造出了這把寶劍，但是真正把它揮舞得得心應手、遊刃有餘的是皮爾遜。在分佈曲線和數據的擬合優度檢驗中，χ 2  分佈可是一個利器，而皮爾遜的這個工作被認為是假設檢驗的開山之作。皮爾遜繼承了高爾頓的衣缽，統計功力深厚，在19世紀末20世紀初很長的一段時間裏，一直被數理統計武林人士尊為德高望重的第一大劍客。

第二位劍客是戈塞特(William Sealy Gosset, 1876-1937)，筆名是大家都熟悉的學生氏 (Student)，而他手中的寶劍是 t   分佈。戈塞特是化學、數學雙學位，依靠自己的化學知識進釀酒廠工作，工作期間考慮釀酒配方實驗中的統計學問題，追隨卡爾.皮爾遜學習了一年的統計學，最終依靠自己的數學知識打造出了t 分佈這把利劍而青史留名。  1908年，戈塞特提出了正態樣本中樣本均值和標準差的比值的分佈，並給出了應用上極其重要的第一個分佈表。戈塞特在t 

第三位劍客是費希爾(Ronald Aylmer Fisher, 1890-1962)，手持F 分佈這把寶劍，在一片荒蕪中開拓出方差分析的肥沃土地。 F 分佈就是為了紀念費希爾而用他的名字首字母命名的。費希爾劍法飄逸，在三位劍客中當屬費希爾的天賦最高，各種兵器的使用都得心應手。費希爾統計造詣極高，受高斯的啓發，系統的創立了極大似然估計劍法，這套劍法現在被尊為統計學參數估計中的第一劍法。

費希爾還未出道，皮爾遜已經是統計學的武林盟主了，兩人歲數相差了33歲，而戈塞特介於他們中間。三人在統計學擂台上難免切磋劍術。費希爾天賦極高，年少氣盛；而皮爾遜為人強勢，佔着自己武林盟主的地位，難免固執己見，以大欺小；費希爾着實受了皮爾遜不少氣。而戈塞特性格温和，經常在兩位大俠之間調和。畢竟是長江後浪推前浪，一代新人換舊人，在眾多擂台比試中，費希爾都技高一籌，而最終取代了皮爾遜成為數理統計學第一大劍客。

由於這三大劍客和統計三大分佈的出現，正態分佈在數理統計學中不再是一枝獨秀，數理統計的領地基本上是被這三大分佈搶走了半壁江山。不過這對正態分佈而言並非壞事，我們細看這三大分佈的數學細節: 假設獨立隨機變量 Xi ∼N(0,1),Yj ∼N(0,1)(i=1⋯n,j=1⋯m) ，則滿足三大分佈的隨機變量可以如下構造出來

• χ 2 n =X2 1 +⋯+X2 n  
• t=Y1 X2 1 +⋯+X2 n n − − − − − − − − √  
• F=X2 1 +⋯+X2 n n Y2 1 +⋯+Y2 m m  

你看這三大分佈哪一個不是正態分佈的嫡系血脈，χ 2  、 t 、F 這三大分佈最初都是從正態分佈切入進行研究的。所以正態分佈在19世紀是武則天，進入20世紀就學了慈禧太后，垂簾聽政了。或者，換個角度説，一個好漢三個幫，正態分佈如果是孤家寡人恐怕也難以雄霸天下，有了統計學三大分佈作為開國先鋒為它開疆拓土，正態分佈真正成為傲世羣雄的君王。

20世紀初，統計學這三大劍客成為了現代數理統計學的奠基人。以哥塞特為先驅，費希爾為主將，掀起了小樣本理論的革命，事實上提升了正態分佈在統計學中的地位。在數理統計學中，除了以正態分佈為基礎的小樣本理論獲得了空前的勝利，其它分佈上都沒有成功的案例，這不能不讓人對正態分佈刮目相看。在隨後的發展中，相關回歸分析、多元分析、方差分析、因子分析、布朗運動、高斯過程等等諸多概率統計分析方法陸續登上了歷史舞台，而這些和正態分佈密切相關的方法，成為推動現代統計學飛速發展的一個強大動力。

7. 正態魅影

Everyone believes in it: experimentalists believing that it is a mathematical theorem, mathematicians believing that it is an empirical fact.  — Henri Poincaré

如果説，充斥着偶然性的世界是一個紛亂的世界，那麼，正態分佈為這個紛亂的世界建立了一定的秩序，使得偶然性現象在數量上被計算和預測成為可能。傑恩斯在《概率論沉思錄》中提出了兩個問題

1. 為什麼正態分佈被如此廣泛的使用？
2. 為什麼正態分佈在實踐使用中非常的成功？

傑恩斯指出，正態分佈在實踐中成功的被廣泛應用，主要是因為正態分佈在數學方面的具有多種穩定性質，這些性質包括：

• 兩個正態分佈密度的乘積還是正態分佈
• 兩個正態分佈密度的卷積還是正態分佈，也就是兩個獨立正態分佈的和還是正態分佈
• 正態分佈N(0,σ2 ) 的傅立葉變換正規化為密度分佈後還是正態分佈
• 中心極限定理保證了多個隨機變量的求和效應將導致正態分佈
• 正態分佈和其它具有相同均值、方差的概率分佈相比，具有最大熵

前三個性質説明了正態分佈一旦形成,就容易保持該形態的穩定， 蘭登對於正態分佈的推導也表明了，正態分佈可以吞噬較小的干擾而繼續保持形態穩定。後兩個性質則説明，其它的概率分佈在各種的操作之下容易越來越靠近正態分佈。正態分佈具有最大熵的性質，所以任何一個對指定概率分佈的操作，如果該操作保持方差的大小，卻減少已知的知識，則該操作不可避免的增加概率分佈的信息熵，這將導致概率分佈向正態分佈靠近。

正由於正態分佈多種的穩定性質，使得它像一個黑洞一樣處於一箇中心的位置，其它的概率分佈形式在各種操作之下都逐漸向正態分佈靠攏，傑恩斯把它描述為概率分佈中重力現象(gravitating phenomenon)。

我們在實踐中為何總是選擇使用正態分佈呢，正態分佈在自然界中的頻繁出現只是原因之一，傑恩斯認為還有一個重要的原因是正態分佈的最大熵性質。在很多時候我們其實沒有任何的知識知道數據的真實分佈是什麼， 但是一個分佈的均值和方差往往是相對穩定的。因此我們能從數據中獲取到的比較好的知識就是均值和方差，除此之外沒有其它更加有用的信息量。因此按照最大熵的原理，我們應該在給定的知識的限制下，選擇熵最大的概率分佈，而這就恰好是正態分佈。即便數據的真實分佈不是正態分佈，由於我們對真實分佈一無所知，如果數據不能有效提供除了均值和方差之外的更多的知識，按照最大熵的原理，正態分佈就是這時候最佳的選擇。

當然正態分佈還有更多令人着迷的數學性質，我們可以欣賞一下:

• 二項分佈 B(n,p)   在 n 很大逼近正態分佈 N(np,np(1−p)) 
• 泊松分佈 Poisson(λ)   在 λ   較大時逼近正態分佈 N(λ,λ) 
• χ 2 (n)  在 n 很大的時候逼近正態分佈 N(n,2n) 
• t 分佈在 n   很大時逼近標準正態分佈 N(0,1) 
• 正態分佈的共軛分佈還是正態分佈
• 幾乎所有的極大似然估計在樣本量n 增大的時候都趨近於正態分佈
• 克拉美分解定理(之前介紹過)：如果 X,Y   是獨立的隨機變量，且 S=X+Y   是正態分佈，那麼 X,Y 
• 如果 X,Y   獨立且滿足正態分佈N(μ,σ2 ) ,  那麼 X+Y , X−Y 
• 對於兩個正態分佈X,Y ,  如果X,Y   不相關則意味着X,Y 獨立，而正態分佈是唯一滿足這一性質的概率分佈

8. 大道至簡,大美天成

To see a world in a grain of sand And a heaven in a wild flower,  Hold infinity in the palm of your hand And eternity in an hour.

 

X¯ ¯ ¯ =X1 +X2 +⋯+Xn n  

算術平均,極其簡單而樸素的一個式子，被人們使用了千百年，在其身後隱藏着一個美麗的世界，而正態分佈正是掌管這個美麗世界的女神。正態分佈的發現與應用的最初歷史，就是數學家們孜孜不倦的從概率論和統計學角度對算術平均不斷深入研究的歷史。中心極限定理在 1773年棣莫弗的偶然邂逅的時候，它只是一粒普通的沙子，兩百多年來吸引了眾多的數學家，這個渾金璞玉的定理不斷的被概率學家們精雕細琢，逐漸的發展成為現代概率論的璀璨明珠。而在統計學的誤差分析之中，高斯窺視了造物主對算術平均的厚愛，也發現了正態分佈的美麗身影。殊途同歸，那是偶然中的必然。一沙一世界，一花一天國,  算術平均或許只是一粒沙子，正態分佈或許只是一朵花，它們卻包含了一個廣闊而美麗的世界，幾百年來以無窮的魅力吸引着科學家和數學家們。 高爾頓他對正態分佈非常的推崇與讚美,1886 年他在人類學研究所的就職演講中説過一段著名的話：“我幾乎不曾見過像誤差呈正態分佈這麼美妙而激發人們無窮想象的宇宙秩序。如果古希臘人知道這條曲線，想必會給予人格化乃至神格化。它以一種寧靜無形的方式在最野性的混亂中實施嚴厲的統治。暴民越多，無政府狀態越顯現，它就統治得越完美。他是無理性世界中的最高法律。當我們從混沌中抽取大量的樣本，並按大小加以排列整理時，那麼總是有一個始料不及的美妙規律潛伏在其中。”

 

概率學家卡克在他的自述傳記《機遇之謎》(Enigmas of chance: An autobiography) 中描述他與正態分佈的淵源：“我接觸到正態分佈之後馬上被他深深的吸引，我感到難以相信，這個來自經驗直方圖和賭博遊戲的規律，居然會成為我們日常生活數學的一部分。”另一位概率學家 Michel Loéve(1907-1979) 説：“如果我們要抽取列維的概率中心思想，那我們可以這樣説，自從 1919 年以後，列維研究的主題曲就是正態分佈，他一而再再而三的以她為出發點，並且堅決的又回到她…… 他是帶着隨機時鐘沿着隨機過程的樣本路徑作旅行的人。”美國國家標準局的顧問  W. J. Youden 用如下一段排列為正態曲線形狀的文字給予正態分佈極高的評價，意思是説：誤差的正態分佈規律在人類的經驗中具有“鶴立雞羣”的地位，它在物理、社會科學、醫學、農業、工程等諸多領域都充當了研究的指南，在實驗和觀測數據的解讀中是不可或缺的工具。

 

正態誤差態分佈律

幾乎所有的人都或多或少的接觸數學，雖然各自的目的不同，對數學的感覺也不同。工程師、科學家們使用數學是因為他簡潔而實用，數學家們研究數學是因為它的美麗動人。像正態分佈這樣，既吸引着無數的工程師、科學家，在實踐中被如此廣泛的應用，又令眾多的數學家為之魂牽夢繞的數學存在，在數學的世界裏也並不多見。我在讀研究生的時候，經常逛北大未名BBS 的數學板，有一個叫 ukim 的著名 ID 在精華區裏面留下了一個介紹數學家八卦的系列《Heroes in My Heart》，寫得非常的精彩，這些故事在喜歡數學的人羣中也流傳廣泛。最後一個八卦是關於菲爾茲獎得主法國數學家託姆(René Thom)的，它曾經令無數人感動，我也借用來作為我對正態分佈的八卦的結語：

在一次採訪當中，作為數學家的託姆同兩位古人類學家討論問題。談到遠古的人們為什麼要保存火種時，一個人類學家説，因為保存火種可以取暖禦寒；另外一個人類學家説，因為保存火種可以燒出鮮美的肉食。而託姆説，因為夜幕來臨之際，火光搖曳嫵媚，燦爛多姿，是最美最美的……

9. 推薦閲讀

All knowledge is, in the final analysis, history.  All sciences are, in the abstract, mathematics.  All methods of acquiring knowledge are, essentially, through statistics.

在終極的分析中，一切知識都是歷史； 在抽象的意義下，一切科學都是數學；  在理性的基礎上，所有的判斷都是統計學。

— C. R. Rao

本人並非統計學專業人士，只是憑個人興趣做一點知識的傳播。對統計學歷史知識的介紹，專業性和系統性都不是我的目的，我更在乎的是趣味性，因為沒有趣味就不會有傳播。如果讀完這段歷史會讓你覺得正態分佈更加親切，不再那麼遙不可及，那我的目的達到了。如果正態分佈是一滴水，我願大家都能看到它折射出的七彩虹。

本文所使用的大多是二手資料，有些歷史細節並沒有經過嚴格的考證，對於歷史資料一定程度上按照個人喜好做了取捨，本文主要基於如下的資料寫成，對於歷史細節感興趣的，推薦閲讀。

• 陳希孺， 數理統計學簡史，湖南教育出版社，2000
• 蔡聰明，誤差論與最小平方法，數學傳播 21(3):3-13，1994
• 吳江霞，正態分佈進入統計學的歷史演化，2008
• E.T. Jaynes, Probability Theory: The Logic of Science，Cambridge University Press，2003
• Saul Stahl, The Evolution of the Normal Distribution, Mathematics Magazine, 1996
• Kiseon Kim, Georgy Shevlyakov, Why Gaussianity, IEEE Signal Processing Magazine, 2008
• Stephen M. Stigler, The History of Statistics: The Measurement of Uncertainty before, Belknap Press of Harvard University Press, 1990
• L. Le Cam, The Central Limit Theorem Around 1935, Statistical Science 1(1):78-91, 1986
• Hans Fischer, A History of the Central Limit Theorem: From Classical to Modern Probability Theory, Springer, 2010