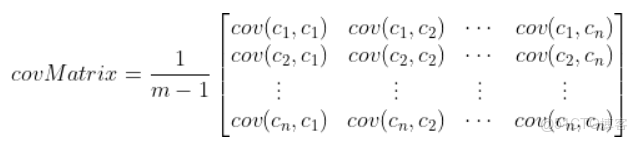聚類分析之K-means算法
文章目錄
- 聚類分析之K-means算法
- 一.距離度量和相似度度量方法
- 1.距離度量
- 2.相似度
- 二.K-means算法原理
- 1.選取度量方法
- 2.定義損失函數
- 3.初始化質心
- 4.按照樣本到質心的距離進行聚類
- 5.更新質心
- 6.繼續迭代 or 收斂後停止
聚類分析是一類非常經典的無監督學習算法。聚類分析就是根據樣本內部樣本“子集”的之間的
特徵找到相似度最接近的一堆堆“子集”,將相似度最接近的樣本各自分為一類。
一.距離度量和相似度度量方法
根據上面的闡述,這個特徵找得好、找的合適,我聚類的效果也就可能更好,那麼一般來説這些特徵是:相似度或者距離,但是一般來説這裏的距離指的是樣本距離。距離一般採用閔可夫斯基和馬氏距離,而相似度則經常採用相關係數和夾角餘弦。
1.距離度量
對於m維度的兩個樣本:
解釋一下:xi,xj是m維度實數樣本空間中的兩個樣本也就是説:
那麼**閔可夫斯基距離(Minkowski distance)**定義為:
用中文解釋一下就是:對於這個樣本在每個維度上的表現(特徵值),進行對應相減並取p次方後相加,求得的和再取1/p次方。至於這個p,其實閔可夫斯基公式具有普適性,也就是説對於不同維度數據集有不同表達,但是都可以寫成這樣的一個通式。
比如説:當p=1、2時,分別退化為曼哈頓距離和歐氏距離:
如果p=無窮大時,則進化為:切比雪夫距離(Chebyshev distance):
下面介紹另外一種距離——馬氏距離(Mahalanobis distance)——馬哈拉諾比斯距離,也是一種衡量各個特徵之間相關性的聚類度量方式,如果我給定一個樣本集合:

可以姑且看作n個樣本m個特徵。其計算公式如下:
其中的S為該樣本集合的協方差矩陣:
其中的c是對於每一個維度(列)而言,用每一列中每一個值分別減去該列的均值,再進行如下計算:
便可以得到協方差矩陣,其中cov是協方差計算。
2.相似度
同樣的,相似度也可以作為聚類指標。常用的就包括兩類——相關係數和夾角餘弦。
相關係數越接近1,那麼兩個樣本就越相似;越接近於0,那麼兩個樣本越不相似。
相關係數公式如下:
中文翻譯一下就是:先用一個樣本在一個維度上的特徵值減去該樣本的所有特徵值均值乘以另一個樣本在該維度上的特徵值減去這個樣本的特徵值均值,將其作為分子。然後分母就是將這兩個樣本進行分別計算各個維度特徵值與均值誤差的平方,各自相加,最後將兩個樣本分別計算的結果相乘。
夾角餘弦也是度量兩個樣本相似度的方法之一:
中文翻譯一下:
將兩個樣本各個維度特徵值相乘後累加得到分子,然後分母就是各自特徵值的平方和,然後相乘。
二.K-means算法原理
import numpy as np
import matplotlib.pyplot as plt
from tqdm import tqdm瞭解了評判指標後,我們就可以開始瞭解k-means算法原理了。
1.選取度量方法
我們選取歐氏距離作為我們的度量方法:
def get_distance(xi,xj):
# 使用歐式距離
"""
xi:第一個樣本
xj:另一個樣本
xi和xj都要有相同形狀大小,(dims,)即一個長為維度數的向量。
輸出:兩個樣本之間的距離
"""
distance = 0
for i in range(len(xi)):
distance += pow( (xi[i]-xj[i]), 2 )
distance = np.sqrt(distance)
return distance2.定義損失函數
我們定義樣本與其所屬的類別中心的距離總和為最終損失函數:
也就是對於每一個類中心:
用集合形式表示所有的質心為:
3.初始化質心
在第一次迭代時,隨機選取k個值作為k個類別的質心。
# 質心初始化函數
def center_init(X,k):
"""
X:是一個(num_sample,dims)的樣本矩陣
k:定義是幾折k-means算法
輸出:質心矩陣(k折(個)長為m的特徵向量)
"""
n,m = X.shape[0],X.shape[1]
centers = np.zeros((k,m))
for i in range(k):
# 隨機從樣本中選取7個實例(樣本記錄)作為k個cluster的質心
center = X[np.random.choice(range(0,n))]
centers[i] = center
return centers4.按照樣本到質心的距離進行聚類
計算每一個樣本到每一個質心的距離,將這個樣本劃分為離它最近的一個類。
# 根據當前的樣本,為單個樣本添加它
# 應該屬於的cluster的類別索引下標
def get_sample_cluster_idx(x, centers):
"""
x:單個樣本實例(記錄)
centers:k個cluster的質心記錄
輸出:
樣本的類別索引下標
"""
closest_i,closest_dist = 0,float('inf') # 初始化最近的索引和距離
# 遍歷每一個(k箇中)質心對於單個樣本的距離
for i,center in enumerate(centers):
distance = get_distance(x, center) # x,center's shape=(dimes,)
if distance < closest_dist:
closest_i = i # 索引下標更新
closest_dist = distance
return closest_i # 返回單個樣本所屬簇下標
# 為每一個簇定義其類別標籤
def build_cluster(centers, k, X):
"""
centers:當前epoch的質心
k:多少個簇
X:樣本矩陣
輸出:
簇列表(shape=(k,-1))——有k個簇列表,每個簇列表存儲的
是樣本序號,表示這個樣本序號i代表的樣本屬於第i類簇。
"""
clusters = [[] for _ in range(k)]
# 枚舉樣本下標和樣本
for x_i, x in enumerate(X):
center_i = get_sample_cluster_idx(x, centers)
# 將當前的樣本序號添加到應該屬於的簇列表
clusters[center_i].append(x_i)
return clusters5.更新質心
對聚類的結果,也就是k個類別,分別計算k個類別的均值並作為新的質心。
# 計算當前的質心並更新
def update_centers(clusters, k, X):
"""
cluster:k個簇列表集合
k:質心個數
X:樣本矩陣
輸出:
更新的質心
"""
m = X.shape[1] # 特徵數
centers = np.zeros((k, m)) # (dims, 特徵數)
# 遍歷當前的簇列表
for i,cluster in enumerate(clusters):
center = np.mean(X[cluster], axis=0)
centers[i] = center
return centers
# 獲取每個樣本所屬的聚類類別
def get_cluster_label(clusters, X):
"""
clusters:當前的簇列表
X:樣本矩陣
"""
y_pred = np.zeros(X.shape[0])
for cluster_i, cluster in enumerate(clusters):
for sample_i in cluster:
y_pred[sample_i] = cluster_i
return y_pred6.繼續迭代 or 收斂後停止
重複4-5步操作,直到聚類後的loss達到了指定要求,或者是其他要求、情況,eg:模型收斂,那麼可以停止訓練並輸出結果;否則就進行下一步的迭代訓練。
# K-means 算法封裝
def kmeans(X, k, epoches):
"""
X:訓練的numpy.ndarray數組
k:質心個數
epoches:迭代次數
"""
# 1.初始化質心
centers = center_init(X,k)
for epoch in tqdm(range(epoches), ncols=150, colour='blue'):
# 2.根據當前質心進行聚類
clusters = build_cluster(centers, k, X)
# 保存當前質心
cur_centers = centers
# 3.更新質心
centers = update_centers(clusters, k, X)
# 4.判斷是否發生變化——是否已經收斂了
diff = centers - cur_centers
if not diff.any():
break
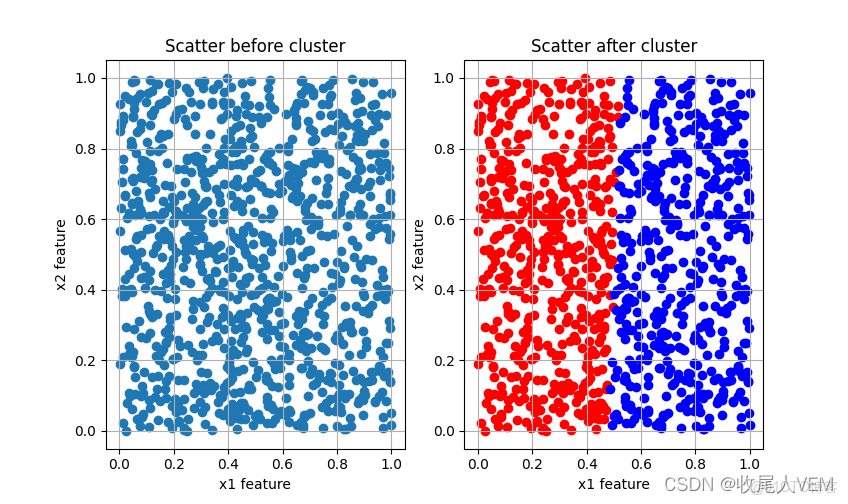
return get_cluster_label(clusters, X)一個2折k-means聚類分析.(基於(1000,2)的隨機隨機數矩陣)