import pandas as pd
from sklearn.metrics.pairwise import linear_kernel
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.feature_extraction.text import TfidfVectorizer
import re
pd.options.display.max_columns = 30
import matplotlib.pyplot as plt
# 支持中文
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用來正常顯示中文標籤
df = pd.read_csv('Seattle_Hotels.csv', encoding="latin-1")
# 數據探索
print(df.head())
print('數據集中的酒店個數：', len(df))
# 創建英文停用詞列表
ENGLISH_STOPWORDS = {
    'i', 'me', 'my', 'myself', 'we', 'our', 'ours', 'ourselves', 'you', "you're", "you've", "you'll", "you'd", 'your', 
    'yours', 'yourself', 'yourselves', 'he', 'him', 'his', 'himself', 'she', "she's", 'her', 'hers', 'herself', 'it', 
    "it's", 'its', 'itself', 'they', 'them', 'their', 'theirs', 'themselves', 'what', 'which', 'who', 'whom', 'this', 
    'that', "that'll", 'these', 'those', 'am', 'is', 'are', 'was', 'were', 'be', 'been', 'being', 'have', 'has', 'had', 
    'having', 'do', 'does', 'did', 'doing', 'a', 'an', 'the', 'and', 'but', 'if', 'or', 'because', 'as', 'until', 'while', 
    'of', 'at', 'by', 'for', 'with', 'about', 'against', 'between', 'into', 'through', 'during', 'before', 'after', 'above', 
    'below', 'to', 'from', 'up', 'down', 'in', 'out', 'on', 'off', 'over', 'under', 'again', 'further', 'then', 'once', 
    'here', 'there', 'when', 'where', 'why', 'how', 'all', 'any', 'both', 'each', 'few', 'more', 'most', 'other', 'some', 
    'such', 'no', 'nor', 'not', 'only', 'own', 'same', 'so', 'than', 'too', 'very', 's', 't', 'can', 'will', 'just', 'don', 
    "don't", 'should', "should've", 'now', 'd', 'll', 'm', 'o', 're', 've', 'y', 'ain', 'aren', "aren't", 'couldn', 
    "couldn't", 'didn', "didn't", 'doesn', "doesn't", 'hadn', "hadn't", 'hasn', "hasn't", 'haven', "haven't", 'isn', 
    "isn't", 'ma', 'mightn', "mightn't", 'mustn', "mustn't", 'needn', "needn't", 'shan', "shan't", 'shouldn', "shouldn't", 
    'wasn', "wasn't", 'weren', "weren't", 'won', "won't", 'wouldn', "wouldn't"
}
def print_description(index):
    example = df[df.index == index][['desc', 'name']].values[0]
    if len(example) > 0:
        print(example[0])
        print('Name:', example[1])
print('第10個酒店的描述：')
print_description(10)
# 得到酒店描述中n-gram特徵中的TopK個
def get_top_n_words(corpus, n=1, k=None):
    # 統計ngram詞頻矩陣，使用自定義停用詞列表
    vec = CountVectorizer(ngram_range=(n, n), stop_words=list(ENGLISH_STOPWORDS)).fit(corpus)
    bag_of_words = vec.transform(corpus)
    """
    print('feature names:')
    print(vec.get_feature_names())
    print('bag of words:')
    print(bag_of_words.toarray())
    """
    sum_words = bag_of_words.sum(axis=0)
    words_freq = [(word, sum_words[0, idx]) for word, idx in vec.vocabulary_.items()]
    # 按照詞頻從大到小排序
    words_freq =sorted(words_freq, key = lambda x: x[1], reverse=True)
    return words_freq[:k]
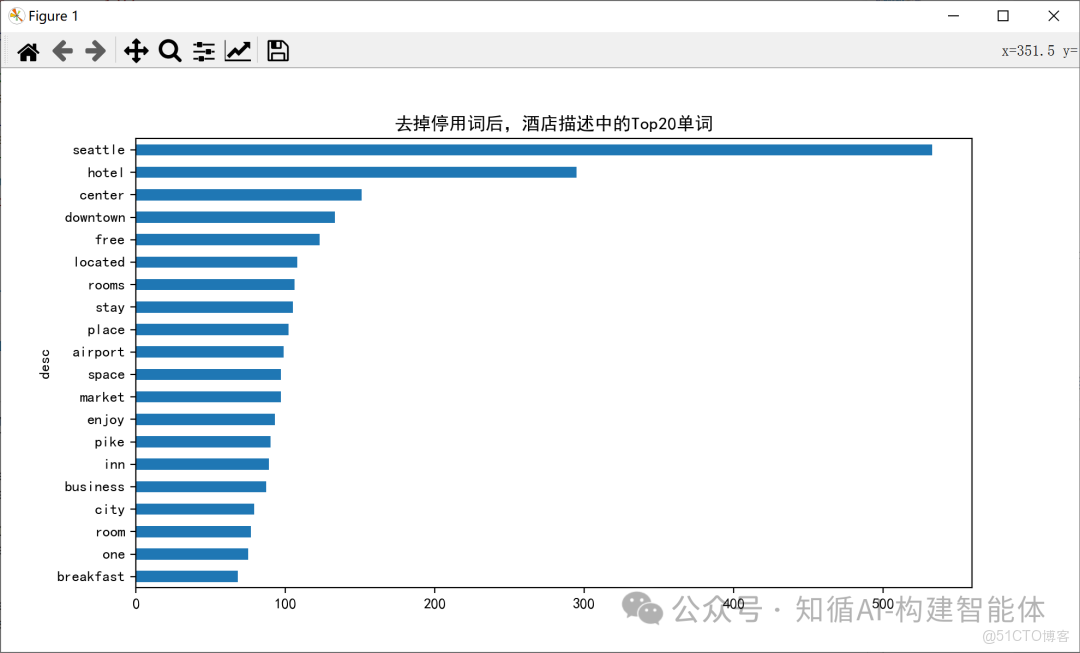
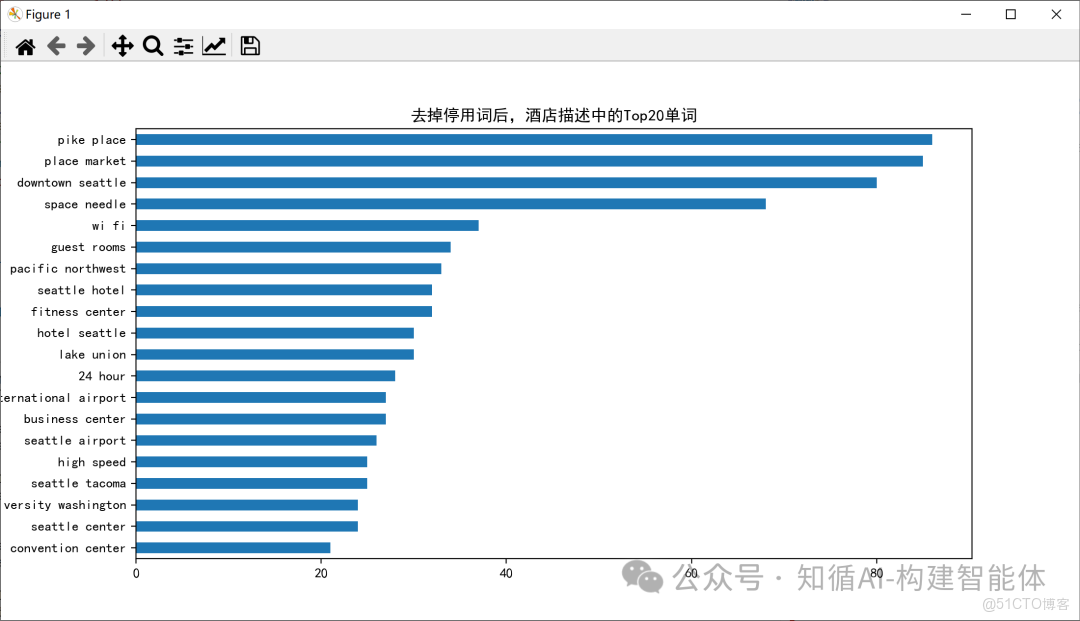
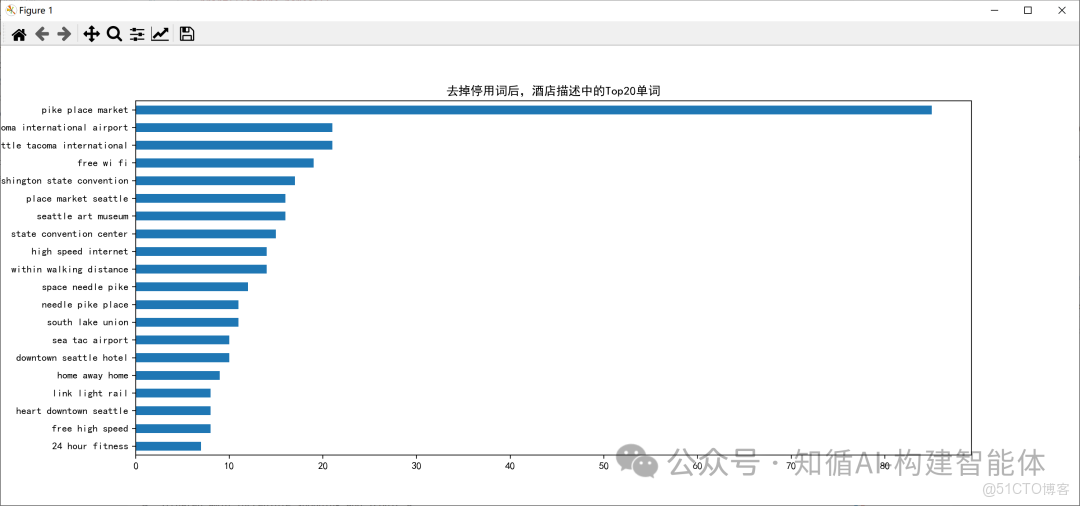
common_words = get_top_n_words(df['desc'], n=2, k=20)
#print(common_words)
df1 = pd.DataFrame(common_words, columns = ['desc' , 'count'])
df1.groupby('desc').sum()['count'].sort_values().plot(kind='barh', title='去掉停用詞後，酒店描述中的Top20單詞')
plt.show()
# 文本預處理
REPLACE_BY_SPACE_RE = re.compile('[/(){}\[\]\|@,;]')
BAD_SYMBOLS_RE = re.compile('[^0-9a-z #+_]')
# 使用自定義的英文停用詞列表替代nltk的stopwords
STOPWORDS = ENGLISH_STOPWORDS
# 對文本進行清洗
def clean_text(text):
    # 全部小寫
    text = text.lower()
    # 用空格替代一些特殊符號，如標點
    text = REPLACE_BY_SPACE_RE.sub(' ', text)
    # 移除BAD_SYMBOLS_RE
    text = BAD_SYMBOLS_RE.sub('', text)
    # 從文本中去掉停用詞
    text = ' '.join(word for word in text.split() if word not in STOPWORDS) 
    return text
# 對desc字段進行清理，apply針對某列
df['desc_clean'] = df['desc'].apply(clean_text)
#print(df['desc_clean'])
# 建模
df.set_index('name', inplace = True)
# 使用TF-IDF提取文本特徵，使用自定義停用詞列表
tf = TfidfVectorizer(analyzer='word', ngram_range=(1, 3), min_df=0.01, stop_words=list(ENGLISH_STOPWORDS))
# 針對desc_clean提取tfidf
tfidf_matrix = tf.fit_transform(df['desc_clean'])
print('TFIDF feature names:')
#print(tf.get_feature_names_out())
print(len(tf.get_feature_names_out()))
#print('tfidf_matrix:')
print(tfidf_matrix.shape)
# 計算酒店之間的餘弦相似度（線性核函數）
cosine_similarities = linear_kernel(tfidf_matrix, tfidf_matrix)
#print(cosine_similarities)
print(cosine_similarities.shape)
indices = pd.Series(df.index) #df.index是酒店名稱
# 基於相似度矩陣和指定的酒店name，推薦TOP10酒店
def recommendations(name, cosine_similarities = cosine_similarities):
    recommended_hotels = []
    # 找到想要查詢酒店名稱的idx
    idx = indices[indices == name].index[0]
    print('idx=', idx)
    # 對於idx酒店的餘弦相似度向量按照從大到小進行排序
    score_series = pd.Series(cosine_similarities[idx]).sort_values(ascending = False)
    # 取相似度最大的前10個（除了自己以外）
    top_10_indexes = list(score_series.iloc[1:11].index)
    # 放到推薦列表中
    for i in top_10_indexes:
        recommended_hotels.append(list(df.index)[i])
    return recommended_hotels
print(recommendations('Hilton Seattle Airport & Conference Center'))
print(recommendations('The Bacon Mansion Bed and Breakfast'))
#print(result)

假設語料庫中有以下句子：
今天天氣真好
今天心情真好
明天天氣不錯
計算P(天氣|今天)：
Count(今天, 天氣) = 1（第1句）
Count(今天) = 2（第1、2句）
P(天氣|今天) = 1/2 = 0.5

from collections import defaultdict, Counter
import numpy as np
# 簡單語料庫
corpus = [
    ['今天', '天氣', '真好'],
    ['今天', '心情', '真好'], 
    ['明天', '天氣', '不錯']
]
# 構建Bigram模型
def build_bigram_model(corpus):
    bigram_counts = defaultdict(Counter)
    unigram_counts = Counter()
    for sentence in corpus:
        for i in range(len(sentence)-1):
            current_word = sentence[i]
            next_word = sentence[i+1]
            bigram_counts[current_word][next_word] += 1
            unigram_counts[current_word] += 1
    # 計算概率
    bigram_probs = {}
    for prev_word, next_words in bigram_counts.items():
        total = unigram_counts[prev_word]
        bigram_probs[prev_word] = {
            next_word: count/total for next_word, count in next_words.items()
        }
    return bigram_probs
# 構建模型
model = build_bigram_model(corpus)
print("P(天氣|今天) =", model['今天']['天氣'])
print("P(心情|今天) =", model['今天']['心情'])

P(天氣|今天) = 0.5
P(心情|今天) = 0.5

def generate_text(seed_word, model, length=10):
    current_word = seed_word
    generated_text = [current_word]
    for _ in range(length-1):
        if current_word not in model:
            break
        next_words = list(model[current_word].keys())
        probabilities = list(model[current_word].values())
        # 按概率選擇下一個詞
        next_word = np.random.choice(next_words, p=probabilities)
        generated_text.append(next_word)
        current_word = next_word
    return ''.join(generated_text)
# 生成文本
print("生成示例:", generate_text('今天', model, 5))

生成示例: 今天天氣真好

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import minimize_scalar
# 設置matplotlib支持中文顯示
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用來正常顯示中文標籤
plt.rcParams['axes.unicode_minus'] = False  # 用來正常顯示負號
# 觀測數據：7次正面，3次反面
data = np.array([1, 1, 1, 1, 1, 1, 1, 0, 0, 0])
n_heads = np.sum(data)
n_tails = len(data) - n_heads
# 定義似然函數
def likelihood(p):
    return p**n_heads * (1-p)**n_tails
# 定義負對數似然函數（因為我們要最小化）
def neg_log_likelihood(p):
    return - (n_heads * np.log(p) + n_tails * np.log(1-p))
# 使用優化方法找到最大似然估計
result = minimize_scalar(neg_log_likelihood, bounds=(0.01, 0.99), method='bounded')
mle_p = result.x
print(f"最大似然估計值: p = {mle_p:.3f}")
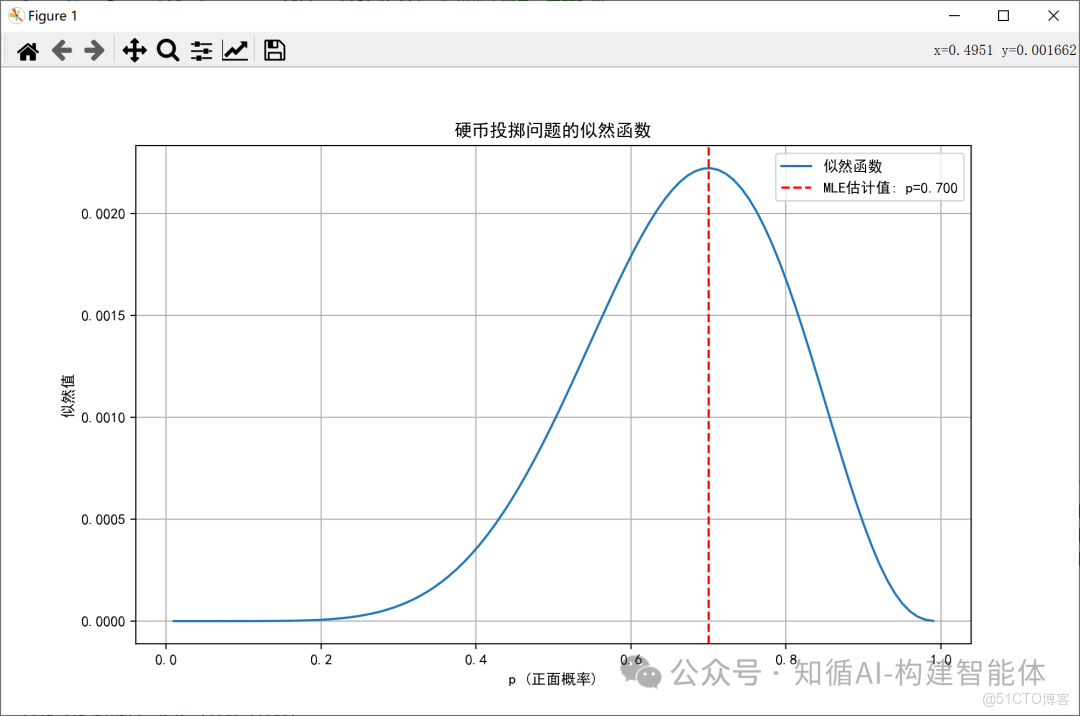
# 可視化似然函數
p_values = np.linspace(0.01, 0.99, 100)
likelihood_values = [likelihood(p) for p in p_values]
plt.figure(figsize=(10, 6))
plt.plot(p_values, likelihood_values, label='似然函數')
plt.axvline(mle_p, color='r', linestyle='--', label=f'MLE估計值: p={mle_p:.3f}')
plt.xlabel('p (正面概率)')
plt.ylabel('似然值')
plt.title('硬幣投擲問題的似然函數')
plt.legend()
plt.grid(True)
plt.show()