一、我需要學習“時間序列”嗎
今天主題是“時間序列模型”,在開始之前我們先討論一下學習大模型需要了解時間序列嗎,首先要看我們的目標,學習大模型也必須也要有自己的目標。
應用型工程師:
如果想成為一名應用大模型的專業工程師,比如構建一個智能聊天客服機器人、開發一個文檔總結工具、創建一個代碼生成助手,那麼,不需要深入研究時間序列模型,此時你的核心技能應該是:
強化提示詞工程:如何設計問題才能從大模型得到最佳答案;
數據處理:如何準備和清洗用於微調的文本數據;
但瞭解後會更強大,理解時間序列能讓你看到一個更廣闊的世界,如果你的項目正好需要分析和預測時間數據(比如分析用户活躍度的趨勢、預測產品未來銷量),或者給大模型喂數據時,經常需要構造具有時間上下文的信息,如果你有時間序列的思維,你會更清楚如何構建這些數據。基於此,對於應用者,時間序列不是入門門檻,但它是一個能讓你從“會用”到“用好”、“用精”的關鍵進階技能。
核心算法研究者:
如果你的目標是深入大模型的原理,甚至參與訓練和創造新的大模型,那麼時間序列的知識就變得至關重要。
- 大模型處理的就是“序列”:大模型的根本任務是處理序列信息,無論是文本序列、代碼序列,還是圖像切塊後的序列。理解ARIMA、RNN、LSTM如何捕捉序列中的依賴關係,會讓你更深刻地理解Transformer為什麼這麼設計。
- 多模態趨勢:大模型不僅僅是語言模型,而是多模態模型。這意味着它們要統一處理文本、圖像、音頻、視頻等各種數據。音頻和視頻本質上是時間序列!音頻是聲波隨時間的變化,視頻是圖像幀隨時間的變化。要讓大模型真正理解和生成流暢的語音和視頻,就必須擁有強大的時間序列建模能力。
- 前沿探索:一個非常前沿的方向就是讓大模型直接處理數值時間序列數據(比如股票價格、傳感器數據)。研究人員正在嘗試將時間序列數據像文本一樣進行“分詞”,然後訓練大模型來理解和預測它們。如果你不懂時間序列,根本無法進入這個領域。
二、什麼是時間序列
時間序列數據是按時間順序索引的一系列數據點。它最大的特點是數據點之間存在依賴關係,即“時間上下文”至關重要。這與傳統的獨立同分布數據截然不同。從每日的股票收盤價、每小時的氣温變化,到每分鐘的網站點擊流,時間序列無處不在。分析它的目的主要有兩個:描述歷史規律(如季節性波動)和預測未來值(如預測明日銷售額)。
用一句話概括:時間序列模型,就是一個“看過去、猜未來”的數學工具。它的核心工作就是:從歷史數據中找出規律,然後用這個規律來預測未來會發生什麼。
一個簡單的例子:賣冰淇淋的小店,想象一下,你開了一家冰淇淋店。
- 你的“歷史數據”是:過去幾年,每天賣了多少冰淇淋。
- 數據裏的“規律”是:
- 趨勢:生意越來越好,每年都比前一年多賣一些。(長期向上)
- 季節性:每年夏天賣的都比冬天多得多;每個週末賣的都比周一到週五多。(週期性波動)
- 突發噪音:突然有一天賣得特別差,因為那天下暴雨了。(無法預測的偶然事件)
- 你現在遇到的“問題”是:下個月我該進多少貨?進多了會化掉,進少了又沒錢賺。
這時,時間序列模型就可以登場了!它會做兩件事:
- 分析歷史:模型會像一位精明的老師傅,仔細研究你過去幾年的銷售記錄,把上面提到的“趨勢”和“季節性”(夏天/週末)這些穩定規律都總結出來。
- 預測未來:老師傅根據總結出的規律,再看看下個月的日曆(有多少個週末?天氣是不是夏天?),然後告訴你:“老闆,根據以往經驗,下個月大概能賣5000盒冰淇淋,你就按這個量進貨吧!”
當然,它沒法預測“下暴雨”這種偶然事件,但它能幫你做出一個基於歷史數據的最優猜測,這遠比你自己憑感覺瞎猜要準確得多!
三、時間序列的核心概念與預處理
- 組成成分:
- 趨勢:數據長期變化的總體方向(上升、下降或平穩)。
- 季節性:在固定週期(如一天、一年)內重複出現的規律波動。
- 週期性:非固定頻率的波動(如經濟週期)。
- 殘差:去除趨勢、季節性和週期後剩下的隨機“噪音”。
- 平穩性:一個平穩的時間序列其統計特性(如均值、方差)不隨時間變化。這是ARIMA等許多模型的基本要求。Augmented Dickey-Fuller (ADF) 檢驗是一種常用的統計檢驗方法,其原假設是“序列非平穩”。如果p值小於顯著性水平(如0.05),則拒絕原假設,認為序列平穩。
- 預處理:差分(用當前值減去前一時刻的值)是消除趨勢和季節性的最強有力工具,常用於將非平穩序列轉換為平穩序列。
四、時間序列模型家族
1. 平滑法
平滑法適合做短期預測,概念簡單。Holt-Winters 模型通過三種成分(水平、趨勢、季節)的平滑方程,能有效地處理具有趨勢和季節性的數據。
示例:使用Holt-Winters模型進行季節性分解與預測
目標:分析一段具有明顯趨勢和季節性的模擬月度銷售數據,並進行預測。
# 導入必要的庫
import pandas as pd # 用於數據處理和操作
import numpy as np # 用於數值計算和數組操作
import matplotlib.pyplot as plt # 用於數據可視化
from statsmodels.tsa.holtwinters import ExponentialSmoothing # 導入Holt-Winters模型
from statsmodels.tsa.seasonal import seasonal_decompose # 導入季節性分解工具
# 1. 創建模擬數據(包含趨勢 + 季節性 + 隨機噪聲)
# 生成100個月度日期範圍,從2018-01-01開始
dates = pd.date_range(start='2018-01-01', periods=100, freq='M')
# 創建線性趨勢成分:從50逐漸增加到150
trend = np.linspace(50, 150, 100)
# 創建季節性成分:使用正弦函數模擬週期性變化(4個完整週期)
seasonality = 10 * np.sin(np.linspace(0, 4*np.pi, 100))
# 創建隨機噪聲成分:均值為0,標準差為5的正態分佈隨機數
noise = np.random.normal(0, 5, 100)
# 將三個成分相加形成最終的時間序列
sales = trend + seasonality + noise
# 將數據轉換為Pandas Series對象,並指定日期索引
ts = pd.Series(sales, index=dates)
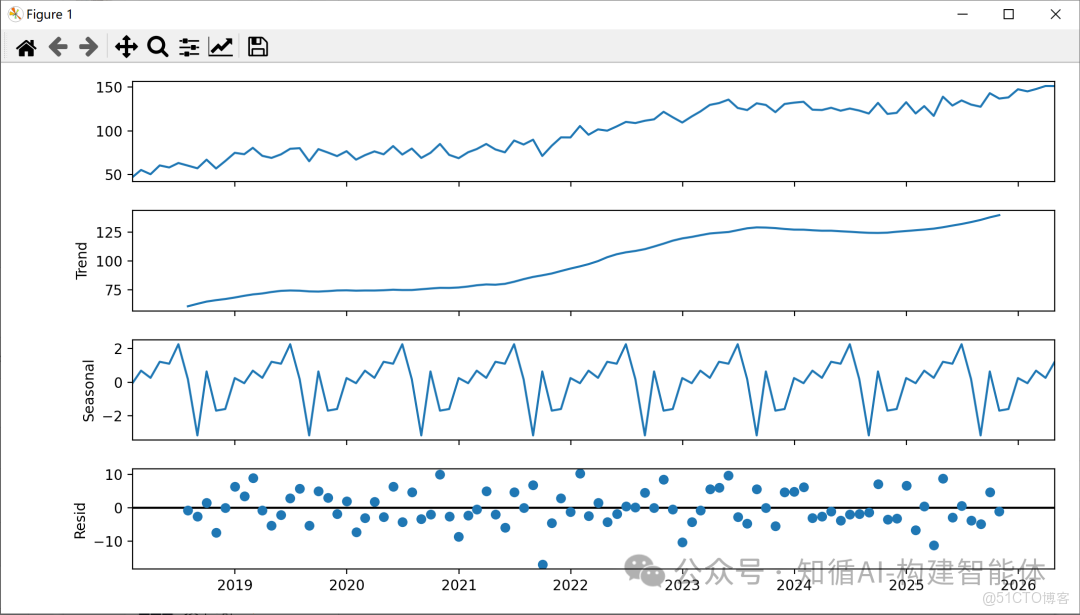
# 2. 可視化 & 季節性分解
# 使用加法模型對時間序列進行分解,得到趨勢、季節性和殘差成分
result = seasonal_decompose(ts, model='additive')
# 繪製分解後的各個成分圖表
result.plot()
# 顯示圖形
plt.show()
# 3. 擬合Holt-Winters模型(使用加法趨勢和加法季節性)
# 創建指數平滑模型,指定趨勢和季節性類型為加法模型,季節性週期為12個月
model = ExponentialSmoothing(ts,
trend='add', # 加法趨勢
seasonal='add', # 加法季節性
seasonal_periods=12) # 一年12個月為一個季節性週期
# 使用數據擬合模型
model_fit = model.fit()
# 4. 進行未來12步(一年)預測
# 使用擬合好的模型預測未來12個時間點的值
forecast = model_fit.forecast(12)
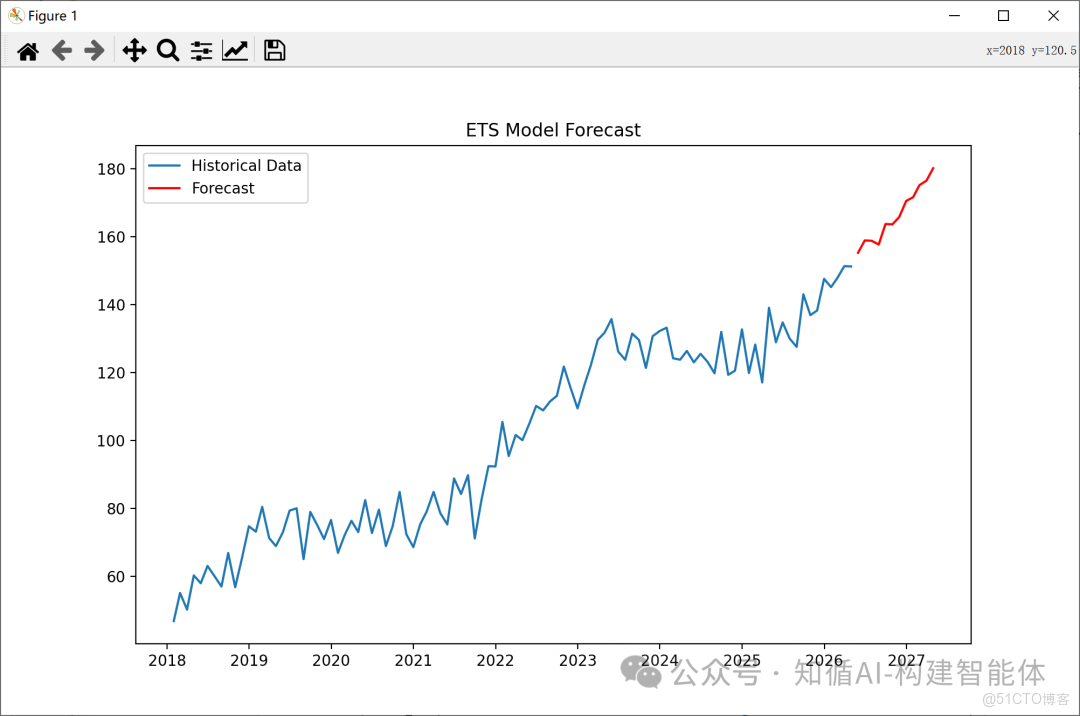
# 5. 繪圖展示歷史數據和預測結果
# 創建一個新的圖形,設置圖形大小
plt.figure(figsize=(10, 6))
# 繪製歷史數據曲線,添加標籤
plt.plot(ts, label='Historical Data')
# 繪製預測數據曲線,使用紅色並添加標籤
plt.plot(forecast, label='Forecast', color='red')
# 添加圖例
plt.legend()
# 添加標題
plt.title('ETS Model Forecast')
# 顯示圖形
plt.show()
代碼分解:
- 數據生成部分:
- trend:線性趨勢,模擬數據的長期變化方向
- seasonality: 季節性成分,使用正弦函數模擬週期性波動
- noise:隨機噪聲,模擬現實世界中的不可預測因素
- 我們創建了一個包含三種成分的模擬時間序列:
- 季節性分解:
- 趨勢(Trend):數據的長期方向
- 季節性(Seasonal):固定週期的重複模式
- 殘差(Residual):去除趨勢和季節性後的隨機波動
- seasonal_decompose 函數將時間序列分解為三個組成部分:
- Holt-Winters模型:
- 使用指數平滑方法,特別適合具有趨勢和季節性的時間序列
- trend='add' 和 seasonal='add' 指定使用加法模型(而不是乘法模型)
- seasonal_periods=12 指定季節性週期為12個月(一年)
- 預測與可視化:
- 使用擬合好的模型預測未來12個月的值
- 將歷史數據和預測結果繪製在同一圖表中,便於比較
這段代碼完整展示瞭如何使用Holt-Winters模型進行時間序列分析和預測,從數據生成到模型擬合再到結果可視化的全過程。
根據銷量數據進行預測:
那麼,Holt-Winters模型中的Trend、Seasonal、Resid該怎麼理解呢?
通過直觀的分析冰淇淋銷量的示例來了解,假設你有一家冰淇淋店,過去三年的每日銷量就是你的時間序列數據。Holt-Winters模型就像一個精明的老師傅,他會把銷量分解成三個部分來看:
1. Trend - 趨勢:代表“大方向”的“戰略家”
- 它是數據在較長時期內表現出來的總體運動方向。它忽略了短期的波動,只看大局。
- 在冰淇淋例子中:
- 上升趨勢:因為你的店口碑很好,附近小區入住的人也越來越多了,所以整體上,生意一年比一年好。今年的平均銷量比去年高,明年的平均銷量預計又會比今年高。這個“逐年變好”的大方向,就是上升趨勢。
- 下降趨勢:如果對面新開了一家更大的競爭對手,導致你的顧客流失,銷量可能呈現下降趨勢。
- 平穩趨勢:如果市場穩定,銷量每年都差不多,那就是平穩趨勢(沒有明顯趨勢)。
- 一句話理解Trend: “我們的生意從長期來看,是在變好、變差,還是維持原樣?”
2. Seasonal - 季節性:代表“週期性規律”的“節律大師”
- 它是在固定週期內重複出現的、規律性的波動。這個週期是已知且固定的。
- 在冰淇淋例子中:
- 年度季節性:毫無疑問,每年夏天的銷量都會達到頂峯,而每年冬天的銷量都會跌入谷底。這個規律年年如此,非常穩定。
- 每週季節性:即使在夏天,每週的週末銷量也會比工作日更高。
- 季節性成分就是把這些固定的、可預測的週期性規律量化出來。 模型會學習到:“哦,在7月份,銷量通常會比年平均水平高出200%;而在1月份,銷量通常會比年平均水平低60%。”
- 一句話理解Seasonal: “在一年四季、一週七天裏,我們的銷量有哪些雷打不動的規律?”
3. Resid - 殘差:代表“隨機噪音”的“意外事件”
- 它是在你剝離了趨勢和季節性這兩個主要規律後,剩下的、無法被解釋的部分。它完全是隨機的、不可預測的“噪音”。
- 在冰淇淋例子中:
- 本來模型預測今天能賣100個冰淇淋(基於“上升趨勢”和“夏天”這個季節性)。
- 但是,今天突然下了一場暴雨,導致實際只賣了30個。
- 又或者,今天突然有個公司跑來團建,一口氣買了200個,導致銷量遠超預測。
- 這場暴雨和這個團建訂單,就是殘差。模型無法提前預測這種突發性的單一事件。
- 一句話理解Resid: “在剔除了所有長期規律和週期規律後,剩下的純粹運氣和意外成分。” 一個理想的模型,其殘差應該是完全隨機的,沒有任何模式可言。如果殘差還有模式,説明有規律沒被模型捕捉到。
總結與聯想
|
成分 |
角色 |
冰淇淋例子 |
關鍵特點 |
|
Trend (趨勢) |
戰略家 |
生意逐年變好 |
看長期大方向 |
|
Seasonal (季節性) |
節律大師 |
夏天旺,冬天淡;週末好,週中差 |
固定的週期規律 |
|
Resid (殘差) |
意外事件 |
某天突然下暴雨或來了個大訂單 |
完全隨機,無法預測 |
所以,Holt-Winters模型就是在做一件事:
從歷史數據中,把這“三重人格”——趨勢、季節性、殘差——一一剝離出來。然後,它把“趨勢”和“季節性”這兩個有規律的成分投射到未來,從而得到對未來的預測。 而“殘差”部分,因為無法預測,就被丟棄了。
2. ARIMA模型
ARIMA模型這是經典方法中的核心和難點。
- AR (AutoRegressive - 自迴歸): “我認為,未來的數據和過去的數據有關係。” 比如,過去幾天賣得好,明天可能也會賣得好。他會用一個公式來描述“過去7天”對“明天”的影響有多大。
- I (Integrated - 積分): 這是個“穩定器”。他發現如果數據一直上升(有趨勢),就很難預測。所以他先把數據做差分處理。
- 差分:今天銷量 - 昨天銷量 = 一個增長值。這樣就把“上升趨勢”轉換成了“在零附近波動”的穩定數據,就好預測多了。
- MA (Moving Average - 移動平均): “我覺得,未來的數據和過去的預測誤差也有關係。” 比如,我昨天預測賣了100個,結果只賣了90個,差了10個。這個“誤差”信息對修正明天的預測也有幫助。
所以,ARIMA就是一個既考慮過去的數據,又考慮過去的誤差,還先把數據變穩定的綜合型偵探。他的升級版叫SARIMA,額外擅長處理季節性問題(比如冰淇淋夏天的銷量規律)。
ARIMA模型就是三者的結合,記為 ARIMA(p, d, q)。SARIMA 在此基礎上增加了對季節性的建模參數 (P, D, Q, S),其中S是季節週期。
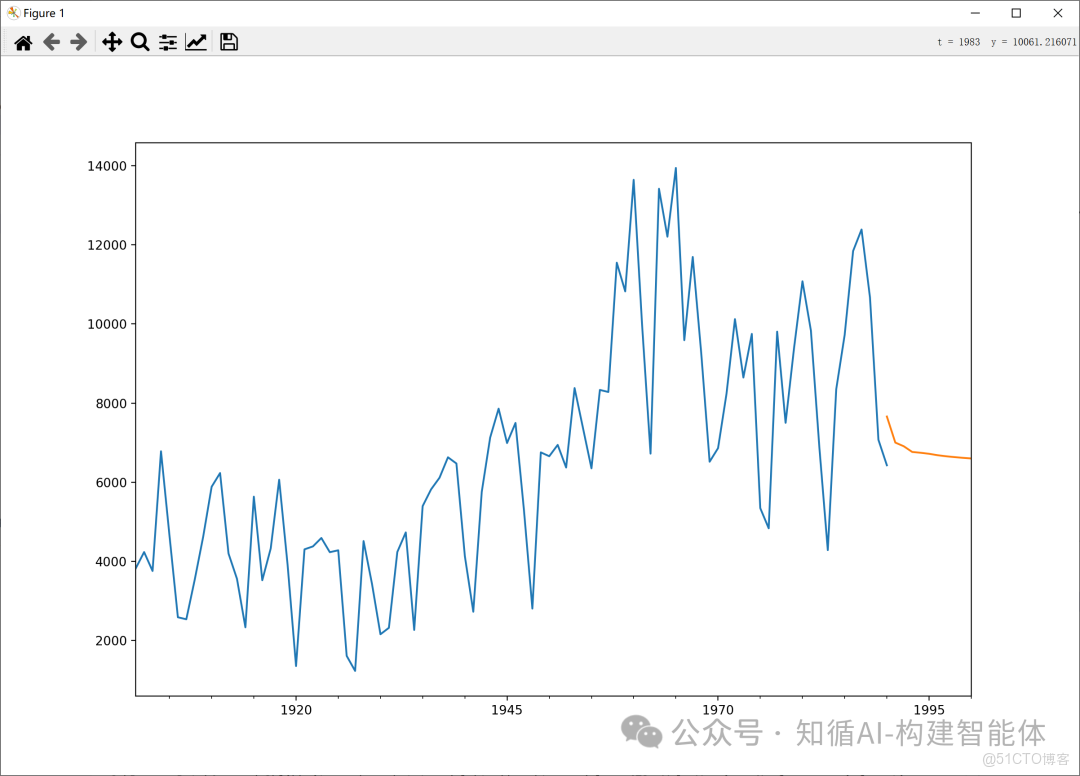
示例:通過ARIMA模型對時間序列進行建模和預測
# 使用ARMA模型進行時間序列預測
import pandas as pd # 數據處理庫
import matplotlib.pyplot as plt # 繪圖庫
import statsmodels.api as sm # 統計模型庫
# 使用新的ARIMA模塊替代已棄用的ARMA(ARIMA(p,0,q)等價於ARMA(p,q))
from statsmodels.tsa.arima.model import ARIMA # ARIMA模型
from statsmodels.graphics.api import qqplot # Q-Q圖繪製工具
# 創建時間序列數據(這裏是一組示例數據)
data = [3821, 4236, 3758, 6783, 4664, 2589, 2538, 3542, 4626, 5886, 6233, 4199, 3561, 2335, 5636, 3524,
4327, 6064, 3912, 1356, 4305, 4379, 4592, 4233, 4281, 1613, 1233, 4514, 3431, 2159, 2322, 4239, 4733,
2268, 5397, 5821, 6115, 6631, 6474, 4134, 2728, 5753, 7130, 7860, 6991, 7499, 5301, 2808, 6755, 6658,
6944, 6372, 8380, 7366, 6352, 8333, 8281, 11548, 10823, 13642, 9973, 6723, 13416, 12205, 13942, 9590,
11693, 9276, 6519, 6863, 8237, 10122, 8646, 9749, 5346, 4836, 9806, 7502, 9387, 11078, 9832, 6886, 4285,
8351, 9725, 11844, 12387, 10666, 7072, 6429]
# 將數據轉換為Pandas Series對象,便於時間序列分析
data = pd.Series(data)
# 為數據創建時間索引(從1901年到1990年,共90個年份)
data_index = sm.tsa.datetools.dates_from_range('1901','1990')
#print(data_index) # 可以打印查看生成的時間索引
# 將時間索引分配給數據
data.index = pd.Index(data_index)
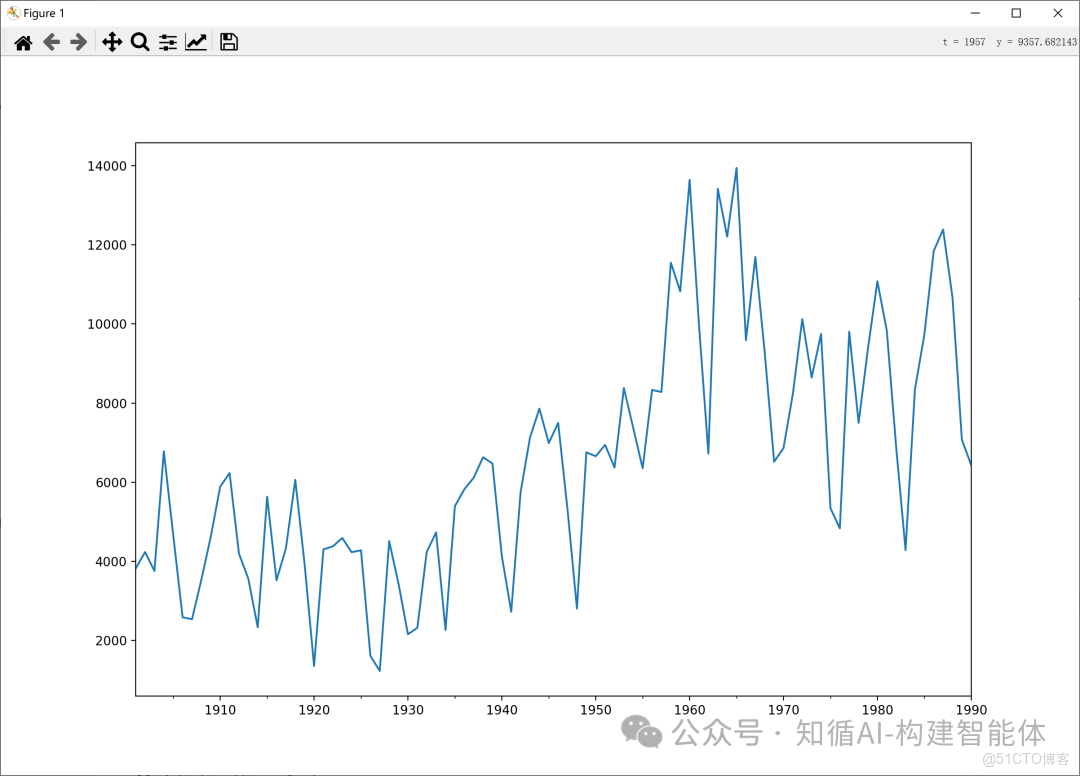
# 繪製原始數據圖,設置圖形大小
data.plot(figsize=(12,8))
plt.title('Original Time Series Data (1901-1990)') # 添加標題
plt.ylabel('Value') # 添加y軸標籤
plt.xlabel('Year') # 添加x軸標籤
plt.show() # 顯示圖形
# 創建ARIMA模型,使用order=(7,0,0)表示ARMA(7,0)模型
# 參數説明:p=7(自迴歸階數), d=0(差分階數), q=0(移動平均階數)
arma = ARIMA(data, order=(7,0,0)).fit() # 擬合模型
# 打印模型的AIC值(赤池信息準則,用於模型選擇,越小越好)
print('AIC: %0.4lf' %arma.aic)
# 使用擬合好的模型進行預測
# 預測時間範圍:從1990年到2000年(共11個時間點)
predict_y = arma.predict(start='1990', end='2000')
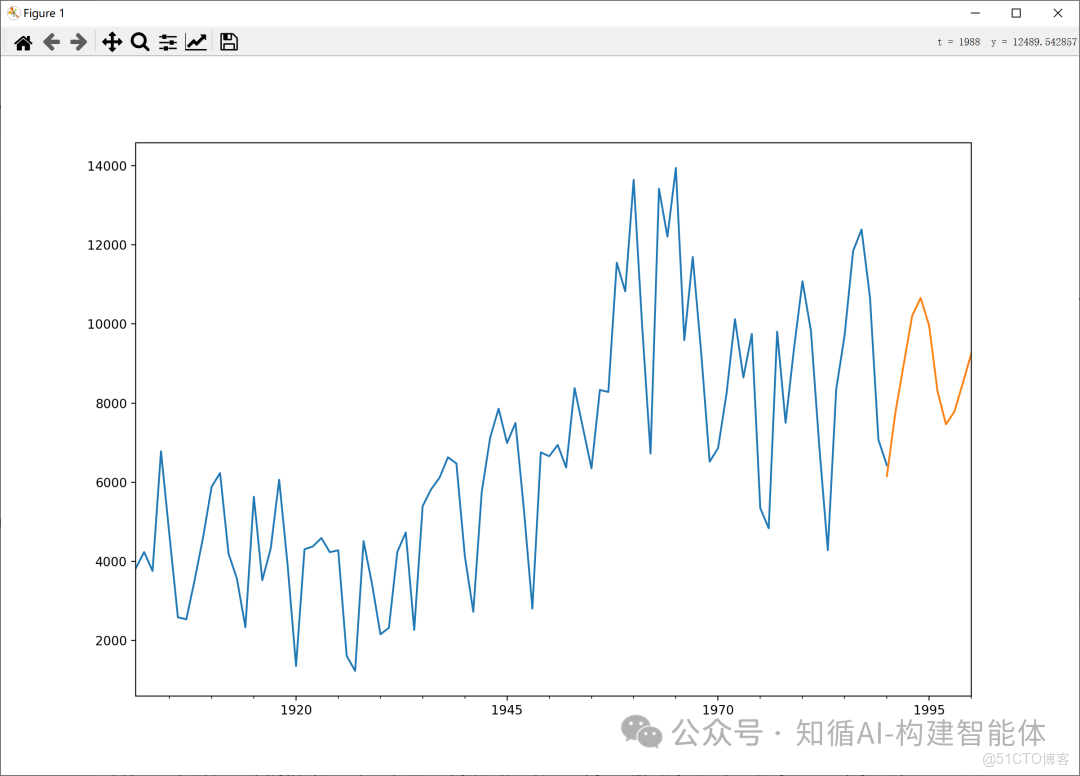
# 繪製預測結果
fig, ax = plt.subplots(figsize=(12, 8)) # 創建圖形和座標軸
ax = data.loc['1901':].plot(ax=ax) # 繪製1901年至今的原始數據
predict_y.plot(ax=ax) # 在同一座標軸上繪製預測值
plt.title('ARMA(7,0) Model Forecast') # 添加標題
plt.ylabel('Value') # 添加y軸標籤
plt.xlabel('Year') # 添加x軸標籤
plt.legend(['Actual Data', 'Forecast']) # 添加圖例
plt.show() # 顯示圖形
代碼説明:
- ARMA模型簡介:
- ARMA(自迴歸移動平均)模型是時間序列分析中的經典模型,由AR(自迴歸)和MA(移動平均)兩部分組成
- ARIMA(p,0,q)等價於ARMA(p,q),其中d=0表示不需要進行差分處理
- 模型參數選擇:
- 代碼中使用order=(7,0,0)表示AR(7)模型(只有自迴歸部分,沒有移動平均部分)
- 在實際應用中,通常需要通過ACF和PACF圖或信息準則(如AIC)來確定最佳的p和q值
- 模型評估:
- AIC(Akaike Information Criterion)用於模型選擇,值越小表示模型擬合越好
- 在實際分析中,還應檢查殘差是否符合白噪聲假設(可以使用QQ圖或Ljung-Box檢驗)
- 預測可視化:
- 代碼將原始數據與預測結果繪製在同一圖表中,便於直觀比較
- 預測區間從1990年到2000年,展示了模型對未來值的預測能力
這段代碼展示瞭如何使用ARMA模型進行時間序列分析和預測的基本流程,包括數據準備、模型擬合、評估和預測可視化。
模型訓練:
結果展示:
AIC: 1616.0337
注意:聲明使用ARIMA模型(其中I(0)表示不使用差分,因此實際上是ARMA模型)對時間序列進行建模和預測;
重點:
示例中的模型的參數order=(7,0,0)是怎麼定義的,為什麼是(7,0,0),而不是其他呢,這裏的AIC值就起到了關鍵的作用,我們把參數值調整為(7,0,7) 試試,首先看看預測結果產生了明顯的偏差,同時AIC值也明顯變大;AIC相對更小,誤差則會更小;
AIC: 1633.3992
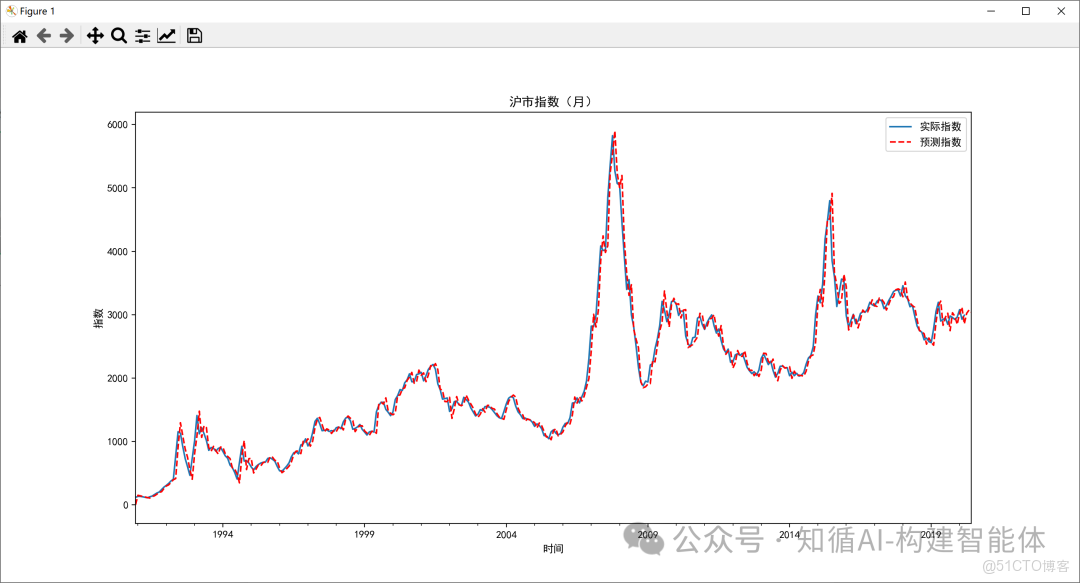
示例:滬市指數預測(最優參數訓練)
使用ARMA工具對滬市指數進行預測:
•第一步,數據加載&探索
按照不同的時間尺度(天,月,季度,年)可以將數據壓縮,得到不同尺度的數據,然後做可視化呈現。
df_month = df.resample('M').mean()
•第二步,模型選擇&訓練,在給定範圍內,選擇最優的超參數
創建ARMA時間序列模型。我們並不知道p和q取什麼值時,可以給它們設置一個區間範圍,比如都是range(0,5),然後計算不同模型的AIC數值,選擇最小的AIC數值對應的那個ARMA模型
•第三步,模型預測,可視化呈現
用這個最優的ARMA模型預測未來3個月的滬市指數走勢,並將結果做可視化呈現。
# 滬市指數走勢預測,使用時間序列ARMA模型
import numpy as np # 數值計算庫
import pandas as pd # 數據處理庫
import matplotlib.pyplot as plt # 繪圖庫
from statsmodels.tsa.arima_model import ARIMA # ARIMA模型(傳統接口)
import statsmodels.api as sm # 統計模型庫
import warnings # 警告處理
from itertools import product # 用於生成參數組合
from datetime import datetime, timedelta # 日期時間處理
import calendar # 日曆功能
# 忽略警告信息
warnings.filterwarnings('ignore')
# 設置matplotlib中文字體顯示
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用來正常顯示中文標籤
plt.rcParams['axes.unicode_minus'] = False # 用來正常顯示負號
# 數據加載
df = pd.read_csv('./shanghai_index_1990_12_19_to_2020_03_12.csv')
# 只保留時間戳和價格兩列
df = df[['Timestamp', 'Price']]
# 將時間列轉換為datetime類型,並設置為索引
df.Timestamp = pd.to_datetime(df.Timestamp)
df.index = df.Timestamp
# 數據探索
# print(df.head())
# 按照不同時間粒度重新採樣:月、季度、年
df_month = df.resample('M').mean() # 按月重採樣並取均值
df_Q = df.resample('Q-DEC').mean() # 按季度重採樣並取均值(季度末為12月)
df_year = df.resample('A-DEC').mean() # 按年重採樣並取均值(年末為12月)
# print(df_month)
# 設置ARIMA模型參數範圍
ps = range(0, 5) # 自迴歸階數(p)的取值範圍
qs = range(0, 5) # 移動平均階數(q)的取值範圍
ds = range(1, 2) # 差分階數(d)的取值範圍,這裏固定為1階差分
# 生成所有可能的參數組合
parameters = product(ps, ds, qs)
parameters_list = list(parameters)
print('parameters_list:', parameters_list)
# 尋找最優ARIMA模型參數,即AIC值最小的模型
results = [] # 存儲所有參數組合及其對應的AIC值
best_aic = float("inf") # 初始化最佳AIC為正無窮
# 遍歷所有參數組合
for param in parameters_list:
try:
# 使用SARIMAX模型(包含季節因素的ARIMA擴展)
model = sm.tsa.statespace.SARIMAX(
df_month.Price, # 時間序列數據
order=(param[0], param[1], param[2]), # (p, d, q)參數
# seasonal_order=(4, 1, 2, 12), # 季節性參數(P, D, Q, S),此處被註釋掉
enforce_stationarity=False, # 不強制要求平穩性
enforce_invertibility=False # 不強制要求可逆性
).fit()
except ValueError:
print('參數錯誤:', param)
continue
aic = model.aic # 獲取模型的AIC值
# 如果當前模型的AIC更小,則更新最佳模型
if aic < best_aic:
best_model = model
best_aic = aic
best_param = param
results.append([param, model.aic]) # 保存當前參數和AIC
# 輸出最優模型摘要信息
print('最優模型: ')
print(best_model.summary())
# 準備預測未來數據
df_month2 = df_month[['Price']] # 只保留價格列
future_month = 3 # 預測未來3個月
# 獲取最後一個月的時間
last_month = pd.to_datetime(df_month2.index[len(df_month2)-1])
date_list = [] # 存儲預測的日期
# 生成未來3個月的日期
for i in range(future_month):
# 計算下個月有多少天
year = last_month.year
month = last_month.month
if month == 12: # 如果是12月,則下個月是明年1月
month = 1
year = year + 1
else:
month = month + 1
# 獲取下個月的天數
next_month_days = calendar.monthrange(year, month)[1]
# 計算下個月的日期
last_month = last_month + timedelta(days=next_month_days)
date_list.append(last_month)
# print('date_list=', date_list)
# 創建未來3個月的空DataFrame,用於存儲預測結果
future = pd.DataFrame(index=date_list, columns=df_month.columns)
# 將未來日期合併到原始數據中
df_month2 = pd.concat([df_month2, future])
# 使用最優模型進行預測
# get_prediction方法返回預測區間,我們使用predicted_mean獲取點預測值
df_month2['forecast'] = best_model.get_prediction(
start=0, # 從第一個數據點開始
end=len(df_month2) # 到最後一個數據點(包括未來預測點)
).predicted_mean
# 繪製滬市指數預測結果
plt.figure(figsize=(30, 7)) # 設置圖形大小
# 繪製實際指數曲線
df_month2.Price.plot(label='實際指數')
# 繪製預測指數曲線(紅色虛線)
df_month2.forecast.plot(color='r', ls='--', label='預測指數')
plt.legend() # 顯示圖例
plt.title('滬市指數(月)') # 設置標題
plt.xlabel('時間') # 設置x軸標籤
plt.ylabel('指數') # 設置y軸標籤
plt.show() # 顯示圖形
經過訓練後的參數預測出的結果展示:
先看看預定參數:
先給定AIC一個基礎值,然後循環每組參數,每次循環得出的AIC和初始AIC比較,將小的AIC值更新並記錄,到下次循環時繼續比較,得出最低的AIC值為止,即可得出最優參數值;
最優模型: SARIMAX Results
==============================================================================
Dep. Variable: Price No. Observations: 352
Model: SARIMAX(1, 1, 4) Log Likelihood -2249.762
Date: Tue, 26 Aug 2025 AIC 4511.524
Time: 20:25:53 BIC 4534.603
Sample: 12-31-1990 HQIC 4520.714
- 03-31-2020
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
ar.L1 0.5618 0.163 3.454 0.001 0.243 0.881
ma.L1 -0.2268 0.164 -1.381 0.167 -0.549 0.095
ma.L2 -0.0453 0.058 -0.783 0.434 -0.159 0.068
ma.L3 -0.1573 0.044 -3.539 0.000 -0.244 -0.070
ma.L4 0.2199 0.031 7.150 0.000 0.160 0.280
sigma2 2.6e+04 941.086 27.632 0.000 2.42e+04 2.78e+04
===================================================================================
Ljung-Box (L1) (Q): 0.01 Jarque-Bera (JB): 1129.88
Prob(Q): 0.94 Prob(JB): 0.00
Heteroskedasticity (H): 2.27 Skew: -0.85
Prob(H) (two-sided): 0.00 Kurtosis: 11.69
===================================================================================
五、總結
時間序列的主要三大用途:
- 預測未來,預測明天股票的漲跌,預測下個月產品的銷量,預測下一小時電力的需求。
- 發現規律,理解數據背後的故事,分析過去十年的氣温數據,看全球變暖的趨勢到底有多嚴重;分析用户訪問APP的數據,發現每週五晚上是流量高峯。
- 檢測異常,實時監控工廠機器的振動數據,一旦發現異常波動,就在它壞掉之前報警;監控你的信用卡消費記錄,一旦出現一筆在國外的異常大額消費(不符合你平時的消費習慣和地點),立刻凍結卡片防止盜刷。
總而言之,時間序列模型就是一個強大的“數據分析師”,它專門處理這種與時間緊密相關的數據,幫助我們從過去中學習,從而更科學地應對未來。 它的目標就是讓我們的決策從“憑感覺”變成“憑數據”。