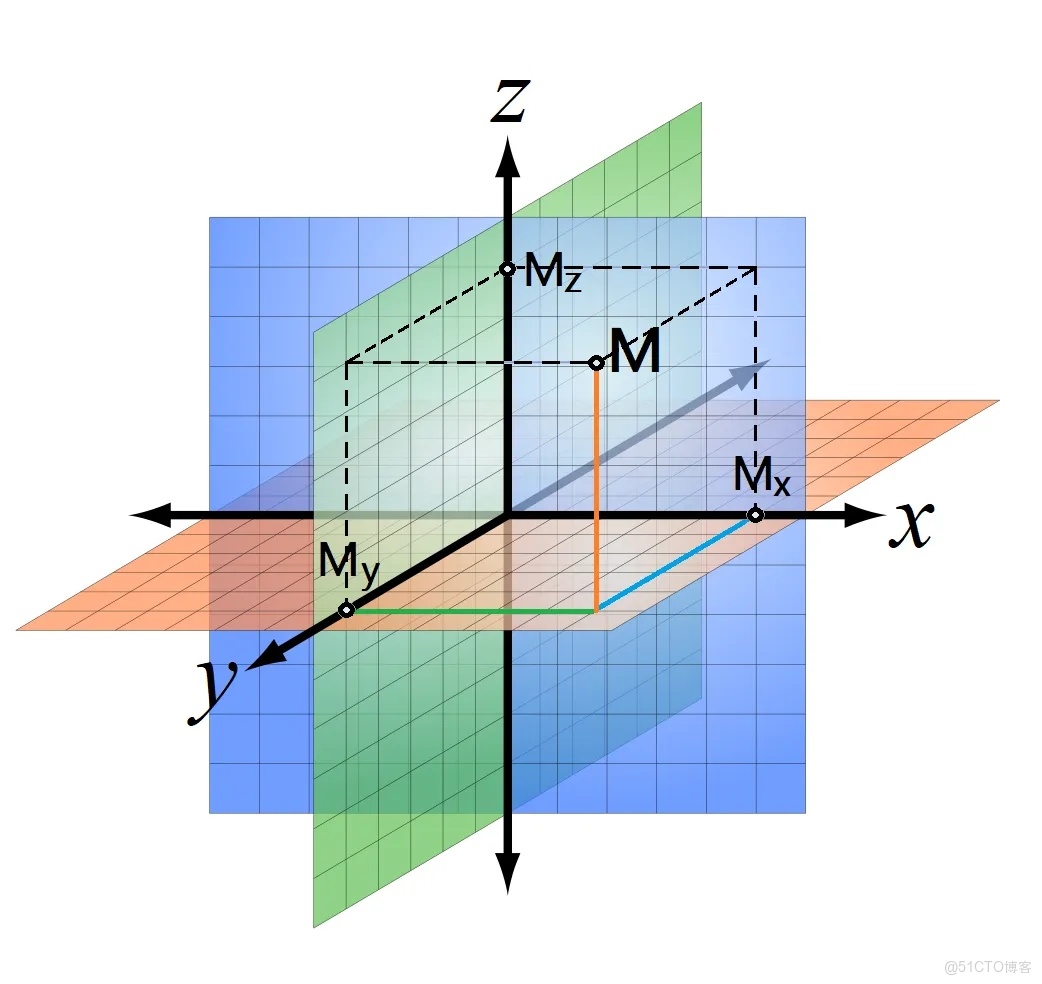
在現代科學與工程的研究中，向量空間理論是分析和建模的基礎工具。從量子力學中的態矢量到信號處理中的特徵提取，再到機器學習中的高維數據表示，向量的結構關係直接決定了系統的複雜性和可分析性。理解向量之間的線性相關性和線性獨立性，不僅是掌握線性代數的關鍵，更是把握信息獨立性和系統完整性的前提。

表面上，線性相關與線性無關似乎只是簡單的數學定義：一組向量能否通過其他向量的線性組合表示。然而，這一概念涉及深刻的數學邏輯、空間結構以及抽象思維。它決定了矩陣秩的上限，影響線性方程組的解的唯一性，也決定了高維數據中冗餘信息的多少。線性無關性意味着每個向量都攜帶獨立信息，而線性相關性則暗示某些向量提供的信息可以由其他向量重構，這種信息結構的識別對於科學建模、算法優化和數據分析至關重要。

當我們面對多個向量組成的系統時，如何判斷它們之間的關係？向量是否能夠完全描述系統狀態？冗餘信息如何影響計算效率和理論推導？這些問題不僅體現了向量空間的數學美感，也直接指導實踐中的計算策略。理解線性相關與線性無關，實質上是理解向量空間的結構和信息獨立性，是現代科學分析中不可或缺的認知工具。

1. 線性相關與線性無關的定義與判定

在向量空間中，向量組 的線性關係是衡量信息獨立性的重要指標。正式定義如下：

定義 1.1（線性相關） 若有不全為零的係數 ，使得

則稱向量組 線性相關。這裏的零向量 是向量空間的零元素，表示“沒有貢獻”的向量。

定義 1.2（線性無關） 若向量組 中僅當所有係數 時，才能使

成立，則稱向量組線性無關。

從定義中可以看到，線性無關性確保每個向量提供獨立信息，而線性相關性意味着向量之間有冗餘。這種判斷是高維數據處理、矩陣運算以及線性系統分析的基礎。例如，在求解線性方程組 時，如果列向量線性相關，矩陣 的秩小於列數，系統可能出現無窮多解或無解；若列向量線性無關，則系統具有唯一解。

判斷向量組是否線性相關常用以下幾種方法：

1. 行列式判定法 對於 個 維向量組成的方陣 ，若
   
   則向量線性無關；若 ，則向量線性相關。
2. 秩判定法 計算矩陣 的秩 ：

• 若 ，向量線性無關；
• 若 ，向量線性相關。

3. 消元法 將向量寫成矩陣形式，通過高斯消元法判斷是否有向量可以由其他向量表示。
4. 係數求解法 嘗試解方程 的非零解，若有，則説明線性相關。

這些方法在數值計算、數據分析和科學建模中具有直接應用意義，為判斷向量獨立性提供可靠手段。

2. 向量空間與基的構建

線性無關性概念的核心應用在向量空間的基構建中。一個向量空間的基是線性無關向量組 ，其線性組合可以覆蓋整個空間。形式上，對於空間中任意向量 ，有唯一系數 使得

這一性質確保基向量能夠完整描述空間中的所有向量，並保證信息不冗餘。

維數定理指出，任意兩個基的向量數量相同，即向量空間的維數 唯一確定。換句話説，向量空間中最多隻能有 個線性無關向量，超過數量的向量必然線性相關。這一定理在高維數據分析和特徵選擇中非常重要：它告訴我們數據的獨立信息量有限，過多特徵可能帶來冗餘而不增加新的信息維度。

在矩陣運算中，向量空間基的概念直接影響秩、特徵值分解和矩陣逆運算。舉例來説，若矩陣 的列向量組成線性無關集合，則 滿秩，矩陣可逆；若列向量線性相關，則秩不足，矩陣不可逆。這一性質在信號處理、機器學習和計算物理中非常關鍵。例如，在迴歸分析中，自變量列的線性相關性（多重共線性）會導致迴歸係數不穩定，而獨立特徵能夠保證模型穩定性和可解釋性。

進一步，從數據降維的角度看，PCA（主成分分析）正是基於向量線性無關的思想：通過尋找數據中線性無關的方向，將原始高維數據映射到低維空間，去掉冗餘信息，同時儘量保留主要的方差信息。這表明線性無關性不僅是數學概念，更是數據處理和特徵提取的核心工具。

3. 判斷線性相關性的常用方法及技術細節

在實際應用中，向量組是否線性相關直接影響計算效率、數據分析和系統建模。

3.1 行列式判定法

對於 個 維向量組成的方陣

行列式 是判斷線性無關性的直接指標：

• 若 ，則向量組線性無關；
• 若 ，則向量組線性相關。

行列式法適合小規模方陣，因為計算複雜度隨維數增長呈指數增加，難以直接用於高維數據或非方陣向量組。對於非方陣情況，需要藉助矩陣秩或奇異值分解方法。

3.2 秩判定法

對於任意矩陣 ，其秩 表示線性無關列向量的最大數量：

判定規則如下：

• 若 ，説明列向量線性無關；
• 若 ，説明列向量線性相關。

矩陣秩的計算通常採用高斯消元法或QR分解、SVD分解等數值穩定方法。例如，使用奇異值分解（SVD）可以將矩陣分解為

其中 為對角矩陣，其非零奇異值個數即為矩陣秩。SVD方法在高維數據分析和科學計算中廣泛應用，因為它能夠精確判定向量獨立性，同時提供量化的冗餘信息指標。

3.3 消元法

消元法是一種操作性強的判定方法。將向量組寫成矩陣形式後，通過行變換或列變換，將矩陣化為行階梯形矩陣（row echelon form）：

在行階梯形矩陣中，每一行的首個非零元素（leading entry）對應一個獨立向量。如果某行完全為零，則説明原矩陣列向量線性相關。消元法的優勢在於直觀、可操作，適用於小規模矩陣和手工計算，同時可以與數值方法結合處理高維數據。

3.4 係數求解法

另一種判定方法是直接解線性組合方程：

將向量寫成矩陣形式 ，其中 是係數向量。判定規則如下：

• 若方程組僅有零解 ，説明向量組線性無關；
• 若方程組有非零解，説明向量組線性相關。

係數求解法是線性代數的基礎原理，在科學計算、工程建模和機器學習特徵分析中都有實際應用。例如，判斷訓練數據特徵向量的獨立性，可以直接通過求解 來判定潛在冗餘特徵。

3.5 方法比較與應用選擇

• 行列式法：適用於小規模方陣，直觀但不適合非方陣或高維數據。
• 秩法：適用範圍廣，數值方法穩定，尤其適合高維數據和科學計算。
• 消元法：操作直觀，可手工實現，也可與數值方法結合，但大規模數據計算複雜度高。
• 係數求解法：概念最直接，與線性方程組求解密切相關，適合算法實現與編程。

在高維數據分析和人工智能特徵選擇中，秩法和奇異值分解（SVD）被廣泛使用，因為它們既能判定向量獨立性，又能量化冗餘信息，為特徵降維和算法優化提供精確依據。

4. 幾何理解

幾何上，線性無關性可以理解為向量在空間中的“獨立方向”。二維空間中，兩條不重合的向量線性無關；三維空間中，三條不共面的向量線性無關。如果向量可以在現有向量的平面或直線中表示，則它們線性相關。

在高維空間中，幾何直觀不再直接可視，但概念仍然成立。線性無關的向量集合構成了高維空間的方向基，而線性相關的向量集合則只能構建低維子空間。這種理解對於數據降維、特徵選擇以及機器學習模型設計至關重要。

5. 線性相關與矩陣運算

矩陣運算中，線性相關與無關直接影響秩、逆矩陣和特徵值分解。當矩陣列向量線性無關時，矩陣滿秩，可以求逆；列向量線性相關時，矩陣秩小於列數，逆矩陣沒有，系統可能有無限解或無解。這一特性在數值計算、最小二乘擬合以及線性方程組求解中非常關鍵。

例如，在迴歸分析中，如果自變量之間線性相關性高（多重共線性），則迴歸係數不穩定，模型預測精度下降。因此，識別和處理線性相關關係是科學計算中不可忽視的步驟。

6. 高維向量空間中的線性相關性

隨着維度增加，向量之間線性相關的可能性增大。例如，在 維空間中，超過 個向量必然線性相關。這一結論來源於維數定理，揭示了高維數據分析中的約束條件。在機器學習中，特徵數量超過樣本數量時，數據矩陣必然有線性相關性，需要通過降維或正則化處理。

高維空間中線性相關性的判斷更依賴於數值方法和矩陣分解，如奇異值分解（SVD）、QR分解等。這些方法不僅提供判定依據，還能定量分析向量之間的相關程度，為算法優化和系統建模提供工具。

7. 線性相關的應用場景分析

線性相關與無關在各類科學問題中都有具體體現：

1. 信號處理 不同信號分量是否線性相關決定了信號混合模型的可分性。獨立信號能夠被分離，而相關信號可能引起信息混淆。
2. 數據分析與降維 主成分分析（PCA）通過尋找線性無關方向，將高維數據映射到低維空間。理解線性相關性能夠有效去除冗餘信息，提升數據處理效率。
3. 物理系統建模 系統狀態變量的線性獨立性關係影響系統的可調控性和可觀測性。線性相關變量可能導致約束條件冗餘，而獨立變量能夠完全描述系統狀態。
4. 計算機科學與機器學習 模型參數之間的線性相關性影響訓練過程的收斂性和模型穩定性。識別獨立特徵可以提高模型泛化能力，並降低過擬合風險。

8. 線性無關性與矩陣分解

矩陣分解技術，如QR分解和SVD，廣泛用於判斷向量組的線性獨立性。QR分解將矩陣分解為正交矩陣 和上三角矩陣 ，通過分析 的對角元素可判斷線性無關性。SVD分解將矩陣分解為三個矩陣 ，通過奇異值判斷向量獨立性和信息量分佈。

這些分解不僅提供判定手段，還能定量分析向量間的冗餘程度，為數據處理、特徵提取和降維提供精確工具。

9. 線性相關與向量空間運算的影響

在線性代數運算中，向量的線性相關性直接影響向量空間的結構：

1. 向量組線性無關，能夠擴展空間維度；
2. 向量組線性相關，構成低維子空間；
3. 矩陣秩受向量線性關係限制；
4. 解線性方程組時，解的唯一性依賴於向量組線性獨立性。

這些原則在科學計算、工程建模和數據分析中都有直接應用。例如，在數值求解大型線性方程組時，識別線性獨立列能夠減少計算量，提高求解效率。

10. 總結與思考

線性相關與線性無關作為向量空間理論的核心概念，其理解不僅涉及抽象數學定義，也直接關聯應用場景中的信息獨立性、計算穩定性和系統結構分析。通過行列式、秩、消元、矩陣分解等方法，可以判斷向量組的線性關係。在高維數據分析、信號處理、物理建模和機器學習等領域，線性無關性是保證系統描述完整性與計算效率的基礎。進一步理解這一概念，能夠幫助科研工作者更精確地識別關鍵變量、優化計算策略，併為理論發展提供嚴謹依據。

線性無關性和相關性不僅是數學工具，也是分析和建模的思維框架。它提醒我們，信息的獨立性決定了系統的完整性，冗餘信息則可能增加複雜度但不增加系統表徵能力。在實際研究和工程實踐中，準確判斷向量關係、理解向量空間結構以及量化信息獨立性，是科學計算和理論分析不可或缺的環節。