核心思想
在標準的模型訓練中,我們通常會將數據集劃分為訓練集和測試集。訓練集用於模型學習參數,測試集用於評估模型的最終性能。
然而,如果測試集本身具有偏差,或者我們想更精細地調整模型(例如超參數調優),僅僅使用一次劃分可能會導致評估結果不夠穩定或具有過高的方差。
交叉驗證的核心目標是: 獲得一個更穩定、更可靠的模型性能估計,減少對特定數據劃分的依賴。
交叉驗證通過多次劃分與多次評估,能更穩健地反映模型的實際性能。
設數據集為
交叉驗證的基本步驟為
- 將數據集 D 劃分為若干個不重疊的子集
- 依次選擇一個子集作為驗證集,其餘 個子集作為訓練集;
- 對每次劃分進行模型訓練與測試,記錄性能指標(如準確率、MSE、F1值等);
- 取所有輪次評估結果的平均值,作為模型總體性能的估計:
其中 表示第 次驗證的誤差或性能指標。
為什麼需要交叉驗證
- 減少過擬合/欠擬合的風險:通過在不同的子集上訓練和測試,可以更全面地瞭解模型對不同數據的適應性。
- 提高評估的可靠性:避免因隨機數據劃分帶來的偶然性影響,使性能度量(如準確率、F1-Score等)的估計值方差更小。
- 有效利用數據:尤其在數據集較小的情況下,交叉驗證能讓每一份數據都至少有一次機會作為測試集來評估模型。
- 模型選擇與超參數調優:它是模型選擇和超參數調優的標準工具。
常見的交叉驗證方法
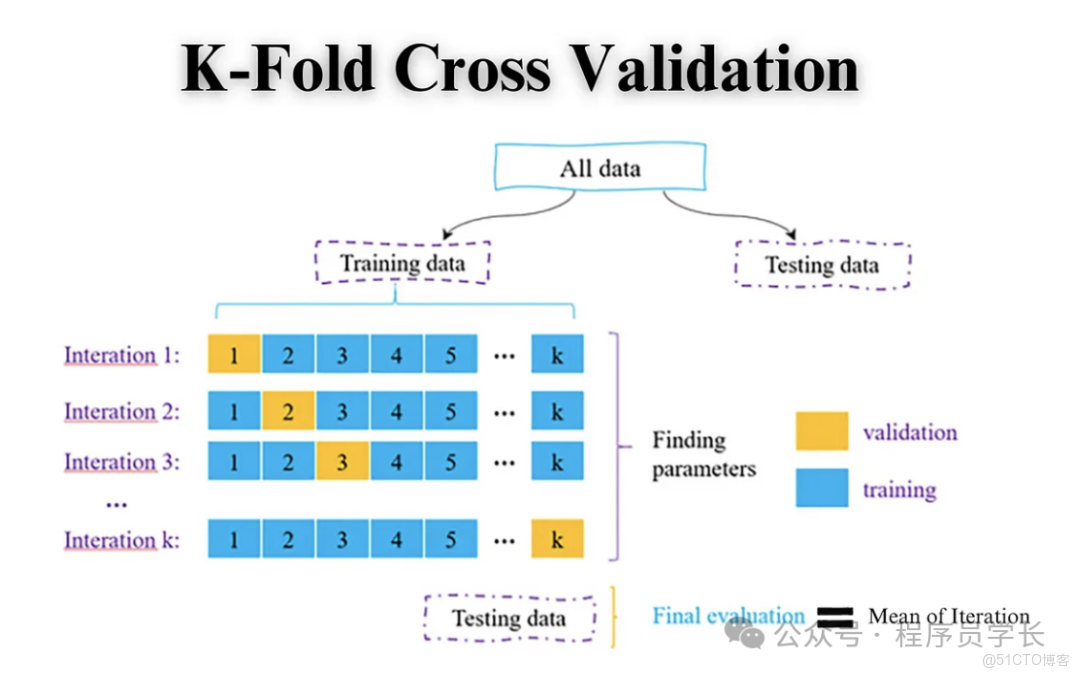
1.K 折交叉驗證
這是最常用的交叉驗證方法。它將數據劃分為 個等大小子集,每次使用其中一個作為驗證集,其餘 個作為訓練集,循環 次。
步驟
- 將原始數據集隨機地劃分為 個大小相等的子集(或稱為“折”,Fold)。
- 重複 次實驗
在第 次實驗中,使用其中 個子集作為訓練集,剩餘的 1 個子集作為驗證集(測試集)。 - 模型在訓練集上訓練,並在驗證集上評估。
- 最終的性能指標是 次評估結果的平均值。
優缺點
- 優點:能夠有效利用所有數據進行訓練和驗證。
- 缺點:需要訓練 個模型,計算成本較高。
from sklearn.model_selection import KFold, cross_val_score
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import load_iris
import numpy as np
# 加載數據
data = load_iris()
X, y = data.data, data.target
# 定義模型
model = LogisticRegression(max_iter=200)
# 定義 K 折交叉驗證(5 折)
kf = KFold(n_splits=5, shuffle=True, random_state=42)
# 計算交叉驗證得分
scores = cross_val_score(model, X, y, cv=kf, scoring='accuracy')
print("每折準確率:", scores)
print("平均準確率:", np.mean(scores))2.留一法交叉驗證
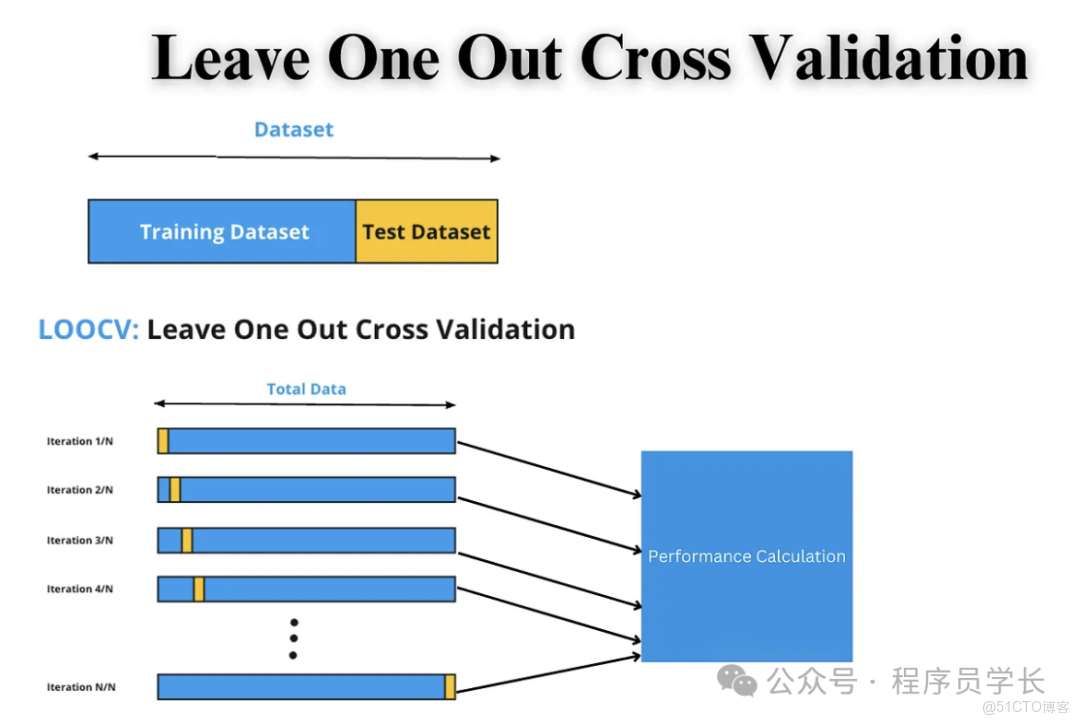
這是 折交叉驗證的極端情況,即 等於數據集中的樣本總數 ,每次只留一個樣本作為驗證集,其他所有樣本作為訓練集。
步驟
- 數據集有 個樣本。
- 重複 次實驗
每次選擇 1 個樣本作為驗證集,剩餘的 個樣本作為訓練集。 - 最終結果是 次評估的平均值。
優缺點
- 優點:充分利用數據,結果幾乎無偏。
- 缺點:計算成本極高(需要訓練 次模型),通常只在樣本量非常小的數據集上使用。
from sklearn.model_selection import LeaveOneOut, cross_val_score
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import load_iris
import numpy as np
# 加載數據
data = load_iris()
X, y = data.data, data.target
# 定義模型
model = LogisticRegression(max_iter=200)
# 留一法交叉驗證
loo = LeaveOneOut()
scores = cross_val_score(model, X, y, cv=loo, scoring='accuracy')
print("樣本數量:", len(scores))
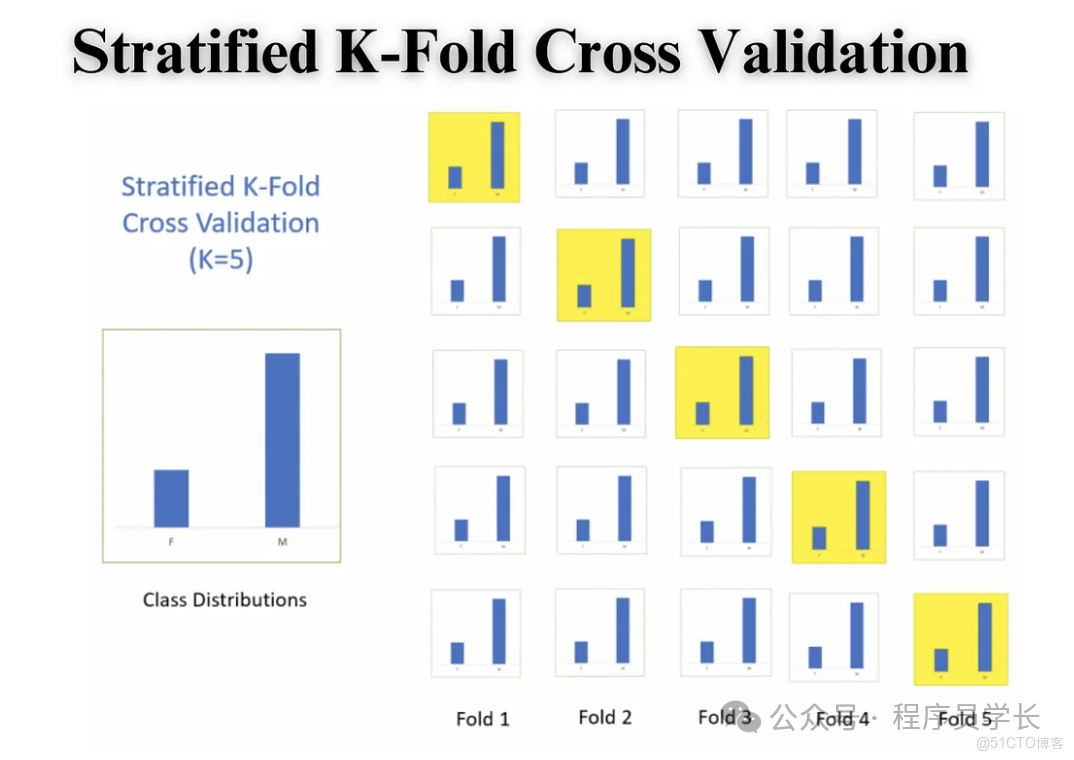
print("平均準確率:", np.mean(scores))3.分層 K 折交叉驗證
主要用於分類問題,特別是當類別分佈不平衡時。
與 K 折交叉驗證類似,但在劃分 折時,它會確保每個子集(折)中各類別樣本的比例與原始數據集中的類別比例大致相同。
例如,如果原始數據中有 90% A 類和 10% B 類,那麼每個 摺子集中也應大致維持 90:10 的比例。
這確保了每次迭代中驗證集和訓練集的類別分佈都具有代表性,有效避免了因隨機抽樣導致的某一折中某一類別樣本過少或缺失的情況。
優點: 在類別不平衡的數據集上,能得到更公平和準確的性能評估。
from sklearn.model_selection import StratifiedKFold, cross_val_score
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import load_iris
import numpy as np
# 加載數據
data = load_iris()
X, y = data.data, data.target
# 定義模型
model = LogisticRegression(max_iter=200)
# 定義分層 K 折交叉驗證
skf = StratifiedKFold(n_splits=5, shuffle=True, random_state=42)
scores = cross_val_score(model, X, y, cv=skf, scoring='accuracy')
print("每折準確率:", scores)
print("平均準確率:", np.mean(scores))4. 重複 K 折交叉驗證
重複 折交叉驗證是為了進一步提高評估的穩定性和可靠性而提出的。
它在 K 折交叉驗證的基礎上,重複多次隨機劃分和驗證,以減少隨機性影響。
步驟
- 設置 (例如 5)和重複次數 (例如 3 次)。
- 執行一次完整的 5 折交叉驗證,記錄 5 個分數。
- 重新隨機劃分數據,再執行一次 5 折交叉驗證,記錄 5 個分數。
- 重複 次,總共得到 個性能分數。
- 最終結果是這所有分數的平均值。
優缺點
- 優點:進一步降低了評估結果的方差,因為它平滑了由單次隨機劃分帶來的偶然性。
- 缺點:計算成本是標準 -Fold 的 倍。
from sklearn.model_selection import RepeatedKFold, cross_val_score
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import load_iris
import numpy as np
# 加載數據
data = load_iris()
X, y = data.data, data.target
# 定義模型
model = LogisticRegression(max_iter=200)
# 定義重複 K 折交叉驗證(5 折重複 3 次)
rkf = RepeatedKFold(n_splits=5, n_repeats=3, random_state=42)
scores = cross_val_score(model, X, y, cv=rkf, scoring='accuracy')
print("所有重複的準確率:", scores)
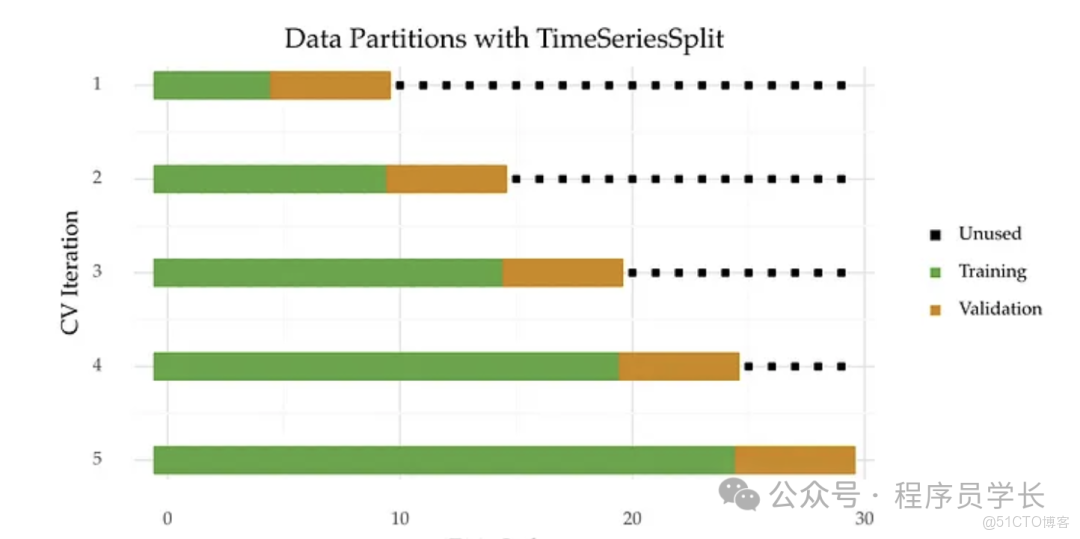
print("平均準確率:", np.mean(scores))5.時間序列交叉驗證
時間序列數據(如股票價格、傳感器讀數、銷售額)有一個固有順序,即時間先後關係。
我們必須保證模型訓練時使用的數據點都早於模型預測時使用的數據點,否則會引入“未來信息”,導致性能虛高。
標準 -Fold CV 因為是隨機劃分,會打亂時間順序,因此不能直接用於時間序列數據。
當數據具有時間依賴性時(如股價、氣温預測),必須使用這種方法。
常用的方法有擴展窗口法和滑動窗口法
擴展窗口法
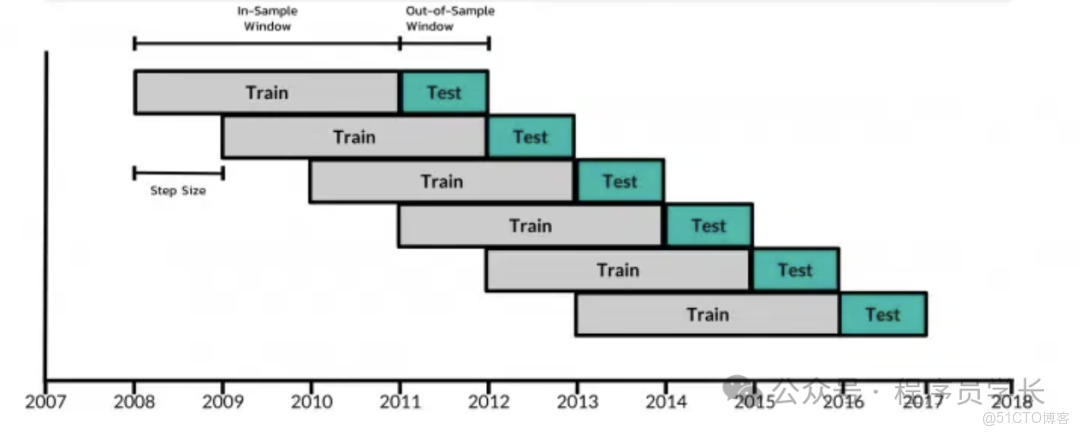
這是時間序列交叉驗證最常見的形式,它模擬了模型隨着時間推移不斷學習更多歷史信息的過程。
核心機制是:訓練集從一個較小的初始歷史窗口開始,並在每一步迭代中持續增加(擴展),以包含之前迭代中用作驗證集的最新數據。
例如
- 第一次訓練使用 到 的數據,驗證 。
- 第二次訓練使用 到 的數據,驗證 。
滑動窗口驗證
滑動窗口策略旨在保持訓練集的大小恆定,它模擬了模型在一個固定長度的歷史信息窗口內進行學習和預測。
例如
- 第一次訓練使用 到 的數據,驗證 。
- 第二次訓練使用 到 的數據,驗證 。·
from sklearn.model_selection import TimeSeriesSplit, cross_val_score
from sklearn.linear_model import LinearRegression
from sklearn.datasets import make_regression
import numpy as np
# 構造時間序列數據
X, y = make_regression(n_samples=100, n_features=1, noise=0.1, random_state=42)
X = np.sort(X, axis=0) # 模擬時間順序
# 定義模型
model = LinearRegression()
# 定義時間序列交叉驗證(5 折)
tscv = TimeSeriesSplit(n_splits=5)
for fold, (train_index, test_index) in enumerate(tscv.split(X)):
print(f"第 {fold+1} 折:")
print(f" 訓練集長度: {len(train_index)}, 驗證集長度: {len(test_index)}")
model.fit(X[train_index], y[train_index])
score = model.score(X[test_index], y[test_index])
print(f" 驗證 R²: {score:.4f}\n")
# 或者直接使用 cross_val_score
scores = cross_val_score(model, X, y, cv=tscv, scoring='r2')
print("平均 R²:", np.mean(scores))