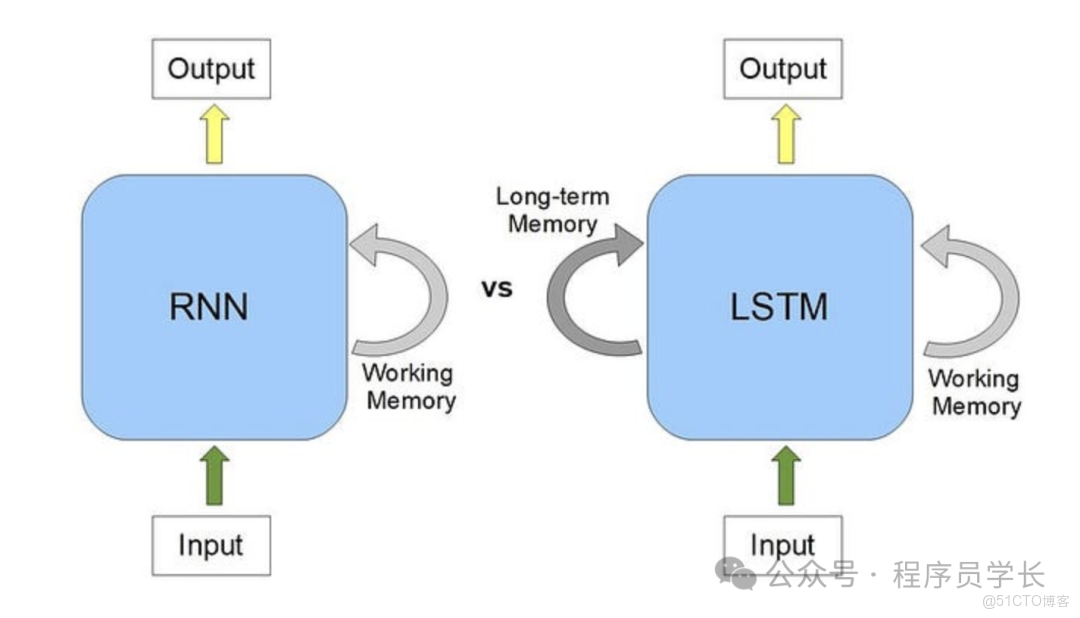
傳統 RNN 結構簡單,但當序列較長時,誤差反向傳播會使梯度逐漸變得極小(梯度消失),導致模型無法學習長期依賴。
LSTM 通過引入精心設計的門控機制來有效地學習、記憶和遺忘信息,從而更好地捕捉序列中的長期依賴關係。
LSTM 核心原理
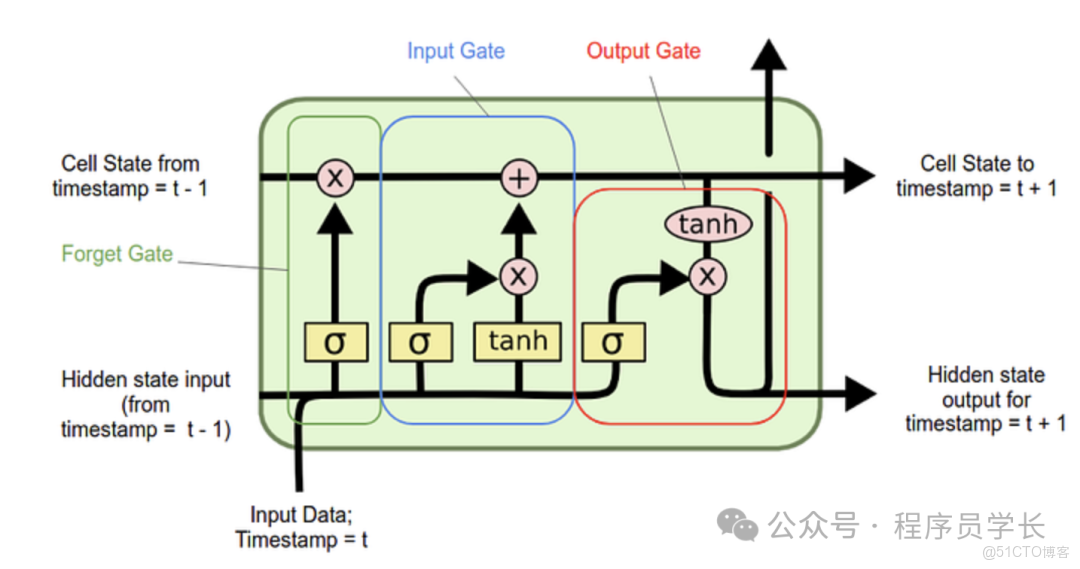
LSTM 的核心是細胞狀態,它就像一條傳送帶,信息在上面直接傳遞,只通過少量的線性操作,這有助於保持信息的完整性,從而解決長期依賴問題。
- 細胞狀態
細胞狀態是 LSTM 的核心。它承載着從序列起點到當前時間步的所有歷史信息,並且只通過簡單的加法和乘法交互,這使得梯度能夠相對穩定地流動,從而解決了梯度消失問題。 - 遺忘門
決定我們應該從上一個細胞狀態 中丟棄哪些信息 - 輸入門
決定哪些新的信息應該加入到細胞狀態 中。 - 輸出門
決定細胞狀態 的哪些部分將被輸出到當前的隱藏狀態 中
數學公式
LSTM 單元在時間步 的計算依賴於上一個時間步 的隱藏狀態 和細胞狀態 ,以及當前時間步的輸入 。
1.遺忘門()
遺忘門決定應該從前一個細胞狀態 中丟棄(遺忘)哪些信息。
數學公式為
其中
- :是 Sigmoid 激活函數,將值壓縮到 。
- 是遺忘門的權重矩陣。
- 是遺忘門的偏置向量。
- 是將上一個隱藏狀態和當前輸入進行拼接。
2.輸入門
決定哪些新的信息應該被添加到細胞狀態 中。它分為兩個部分:
- 輸入門 :決定哪些值需要更新。
- 候選細胞狀態 :創建一個新的候選值向量,準備加入到細胞狀態中。
數學公式為
其中:
- :輸入門的權重和偏置。
- : 候選狀態的權重和偏置。
- : 激活函數,將值壓縮到 。
3.更新細胞狀態()
根據遺忘門和輸入門的結果,更新舊的細胞狀態 為新的 。
原理是
- 將舊狀態 乘以遺忘門 ,丟棄我們決定遺忘的信息。
- 將輸入門 乘以候選狀態 ,這是我們決定添加的新信息。
- 將這兩個結果相加,得到最終的當前細胞狀態 。
4. 輸出門()
決定細胞狀態 的哪些部分將被輸出到當前的隱藏狀態 中(也是下一個時間步的輸入)。
原理是
- 輸出門 決定細胞狀態的哪個部分將作為輸出。
- 將細胞狀態 通過 函數,使其值規範化到 之間。
- 將 與 逐元素相乘,得到最終的隱藏狀態 。
優點
- 解決梯度消失問題
這是 LSTM 最主要的優勢。由於細胞狀態 的更新是通過加法和遺忘門的乘法實現的,其反向傳播的梯度可以更平滑地流回很長的時間步,有效防止了梯度消失。 - 解決長期依賴:通過遺忘門和輸入門,模型可以選擇性地保留或更新信息,使其能夠記憶幾百個甚至更多的步長之前的關鍵信息。
- 靈活的記憶機制:三個門控機制(遺忘、輸入、輸出)賦予了模型強大的控制能力,能夠精確地管理信息流,實現何時遺忘、何時輸入、何時輸出的動態決策。
典型應用
- 自然語言處理 (NLP):機器翻譯、文本生成、情感分析。
- 語音識別:對時序聲學特徵進行建模。
- 時間序列預測:股市預測、氣象預報等。
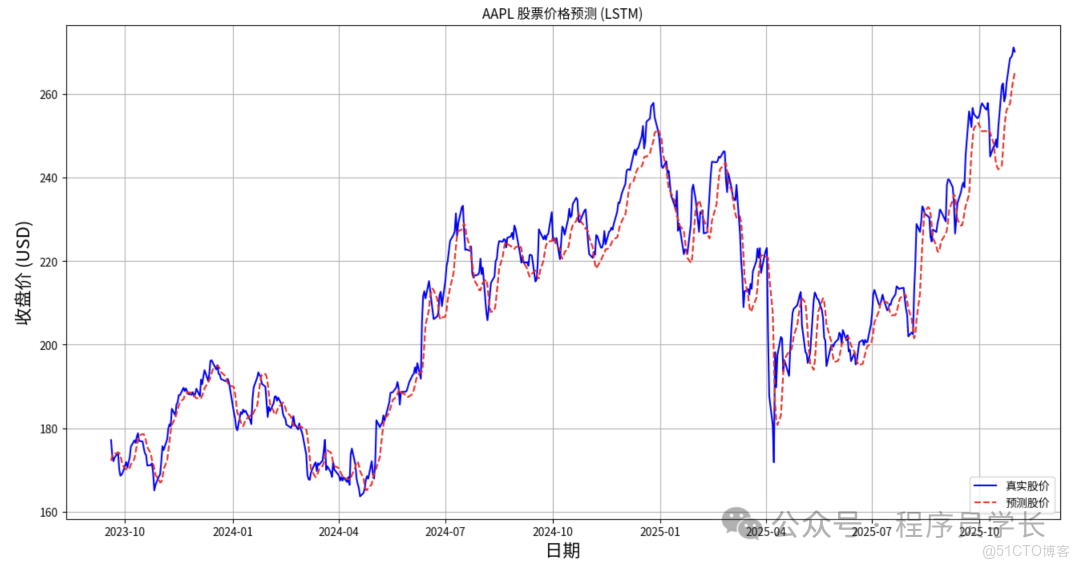
案例分享
下面是一個使用 LSTM 算法預測價格的完整示例代碼。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import yfinance as yf
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_error
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import LSTM, Dense
# --- 1. 數據加載 ---
TICKER = 'AAPL'
START_DATE = '2015-01-01'
END_DATE = '2025-11-01'
print(f"--- 正在下載 {TICKER} 數據 ({START_DATE} 至 {END_DATE}) ---")
try:
# 使用 yfinance 獲取數據
data = yf.download(TICKER, start=START_DATE, end=END_DATE)
# 僅使用 'Close' (收盤價) 作為特徵
dataset = data['Close'].values.reshape(-1, 1)
except Exception as e:
print(f"數據下載失敗: {e}")
exit()
# --- 2. 數據預處理 ---
# 規範化數據 (MinMaxScaler 將數據縮放到 0 到 1 之間)
scaler = MinMaxScaler(feature_range=(0, 1))
scaled_data = scaler.fit_transform(dataset)
# 定義序列長度 (Lookback Window)
# 意思是使用前 N 天的數據來預測第 N+1 天的收盤價
LOOKBACK = 60
# 創建序列數據集
def create_dataset(data, lookback=1):
X, Y = [], []
for i in range(len(data) - lookback):
a = data[i:(i + lookback), 0]
X.append(a)
Y.append(data[i + lookback, 0])
return np.array(X), np.array(Y)
X, Y = create_dataset(scaled_data, LOOKBACK)
# 調整 X 的形狀以適應 LSTM 輸入:[樣本數, 時間步, 特徵數]
# 在本例中:[樣本數, 60, 1]
X = np.reshape(X, (X.shape[0], X.shape[1], 1))
# 劃分訓練集和測試集
# 我們使用 80% 的數據進行訓練
train_size = int(len(X) * 0.8)
X_train, X_test = X[:train_size], X[train_size:]
Y_train, Y_test = Y[:train_size], Y[train_size:]
print(f"總樣本數: {len(X)}")
print(f"訓練集樣本數: {len(X_train)}")
print(f"測試集樣本數: {len(X_test)}")
# --- 3. 構建 LSTM 模型 ---
print("--- 正在構建 LSTM 模型 ---")
model = Sequential()
# 第一層 LSTM: 50 個神經元, 返回序列以便於下一層 LSTM 連接
model.add(LSTM(units=50, return_sequences=True,
input_shape=(X_train.shape[1], 1)))
# 第二層 LSTM: 50 個神經元
model.add(LSTM(units=50))
# 輸出層: 預測一個值 (收盤價)
model.add(Dense(units=1))
# 編譯模型
model.compile(optimizer='adam', loss='mean_squared_error')
# --- 4. 模型訓練 ---
print("--- 正在訓練模型 (約需 10-30 秒) ---")
# epochs: 迭代次數, batch_size: 每次梯度更新使用的樣本數
history = model.fit(X_train, Y_train, epochs=25, batch_size=32, verbose=1)
# --- 5. 模型預測與評估 ---
# 在測試集上進行預測
predictions = model.predict(X_test)
# 將預測結果和真實值反規範化到原始股價尺度
predictions = scaler.inverse_transform(predictions)
Y_test_inverse = scaler.inverse_transform(Y_test.reshape(-1, 1))
# 計算均方根誤差 (RMSE) 作為評估指標
rmse = np.sqrt(mean_squared_error(Y_test_inverse, predictions))
print(f"\n均方根誤差 (RMSE): ${rmse:.4f}")
# --- 6. 結果可視化 ---
# 提取用於可視化的實際日期
train_data_len = data.shape[0] - len(Y_test) - LOOKBACK
test_dates = data.index[train_data_len + LOOKBACK:]
# 創建 DataFrame 方便繪圖
predict_df = pd.DataFrame(data={'Actual': Y_test_inverse.flatten(),
'Predicted': predictions.flatten()},
index=test_dates)
plt.figure(figsize=(16, 8))
plt.title(f'{TICKER} (LSTM)')
plt.xlabel('日期', fontsize=16)
plt.ylabel('收盤價 (USD)', fontsize=16)
# 繪製真實值
plt.plot(predict_df['Actual'], label='真實股價', color='blue')
# 繪製預測值
plt.plot(predict_df['Predicted'], label='預測股價', color='red', linestyle='--')
plt.legend(loc='lower right')
plt.grid(True)
plt.show()