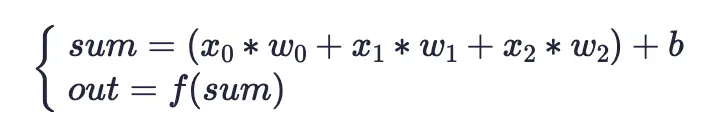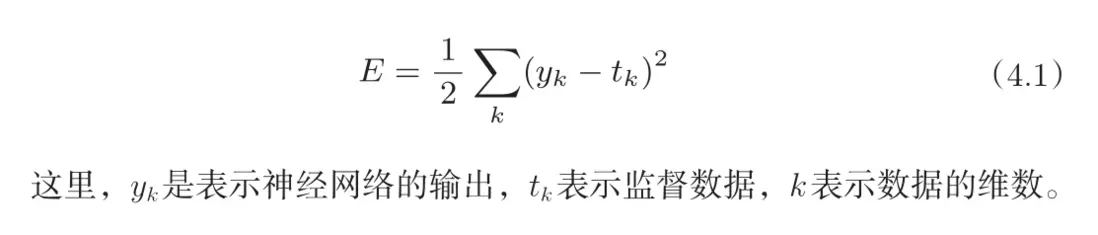【USparkle專欄】如果你深懷絕技,愛“搞點研究”,樂於分享也博採眾長,我們期待你的加入,讓智慧的火花碰撞交織,讓知識的傳遞生生不息!
你一定聽説過神經網絡的大名,你有想過將它用於遊戲AI的行為決策上嗎?其實在(2010年發佈的)《最高指揮官2》中就有應用了,今天請允許我班門弄斧一番,與大家一同用C# 實現最經典的神經網絡 —— 多層感知機(Multilayer Perceptron,簡稱MLP)。
一、前言
神經網絡或者深度學習,總給人一種「量子力學」的感覺,總感覺它神秘無比,又無所不能。我未學習神經網絡之前,總以為它是某種能夠修改自身代碼的代碼,否則怎麼能做到從「不會」變成「會」的呢?但在親自學習後才會明白,它並沒有做到這種地步,但依舊十分神奇。多層感知機是最基礎的神經網絡,很多其它類別的神經網絡都是在這之上的變形。可以説,學會它是邁入深度學習的第一步。
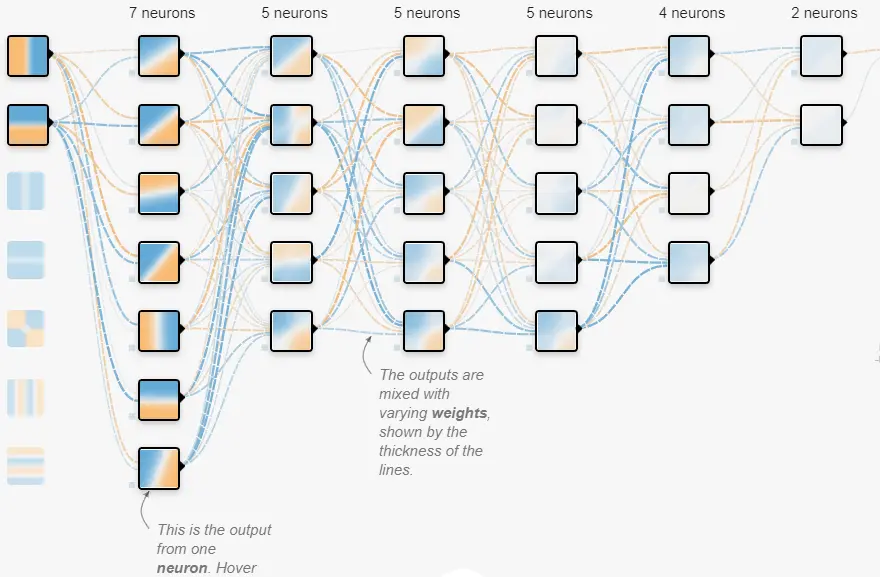
多層感知機雖説經典,但並不過時。提到神經網絡,大多數人腦海裏想到的大概也就是類似這樣的圖片:
這就是一張典型的多層感知機結構圖,看着好像很複雜,但實現它所需要用到的數學原理和編程知識都不難,早年間,研究神經網絡的學者們還用C語言實現呢!
二、什麼是多層感知機
現在進入正題,我們先來簡單講講MLP的原理(如果你對此十分熟悉,只是對代碼實現感興趣,那可以跳過這部分)。
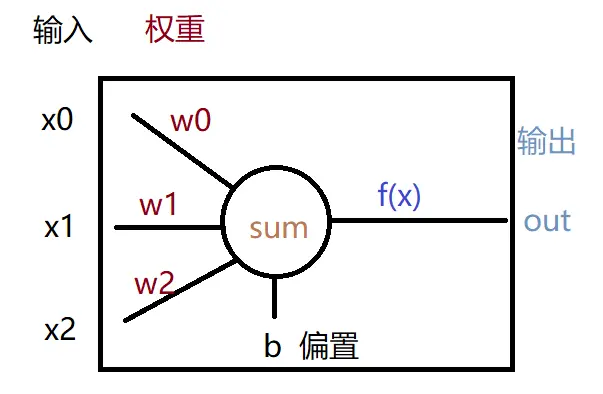
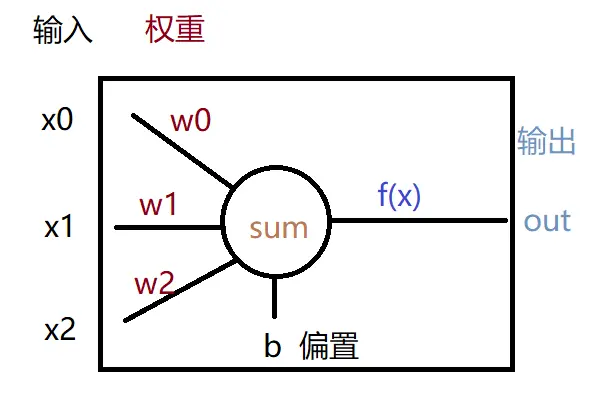
既然叫「多層感知機」,那有單個的感知機嗎?那是自然,單個感知機的結構十分簡單:
它其實就是個算式(為方便理解,我將其分成兩部分):
將傳入感知機的多個輸入x,與對應的權重w相乘(輸入的數量與權重的數量是一樣的,且數量是任意的,本例中用了3個),再加上偏置b就可以得出一個計算值sum。再將這個計算值傳入一個函數f(x)就可得到感知機的最終輸出out。
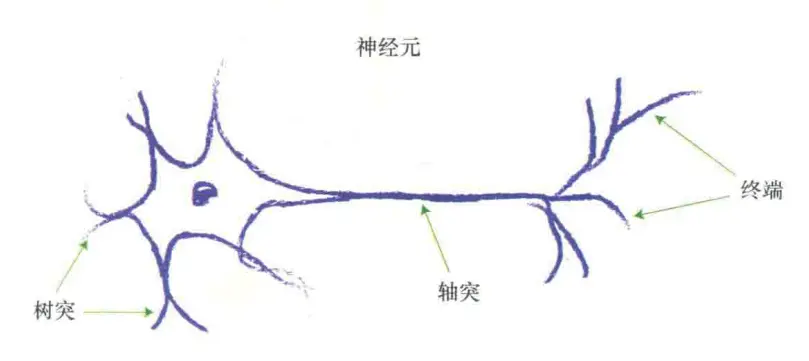
相信你肯定能理解,只是可能對f(x)函數有些好奇,它具體內容是什麼呢?這個函數也被稱為「激活函數」,為什麼叫這個名字?這就得提感知機的另一個名字 —— 人工神經元。其實感知機正是受神經元結構啓發而被提出來的:
神經元會通過樹突接受輸入信號並彙總,而神經元對於各個輸入刺激的響應強度並不相同,所以我們給各個輸入設置了相應權重來模擬這個現象。之後,將處理的信息通過軸突傳給末梢(終端)。但實際上,只有彙總的信號強度大於一定程度時神經元才會向末梢傳遞信號,而模擬這個現象的就是「激活函數」。
那偏置b又是模擬什麼的?其實它是從數學角度考慮的、方便調整輸入加權和的變量值而已。
既然感知機被稱為「人工神經元」,那多層感知機豈不就是「人工神經網絡」?一點沒錯,我們現在所説的「神經網絡」,基本都是指人工神經網絡,而不是真正的、生物的神經網絡。而「神經網絡」起初就是指多層感知機,只不過現在種類多了,定義也變寬泛了。
結合我們對單個感知機的認識,再看看多層感知機:
![]http://uwa-ducument-img.oss-cn-beijing.aliyuncs.com/Blog/Uspa...)
但這裏的單個感知機(後面用「神經元」來代稱)怎麼輸出了多個值(看標藍色的那部分)?這種結構圖可能會誤導某些人,我做個解釋,這裏的每一條線並不是輸出,可以看到它是有箭頭的,每條線表示它所指向的那個神經元的一個權重。加上箭頭是為了表示數據傳遞的方向。
不難看出,它就是將多個感知機以層為單位進行了組合,每層都有任意數量(每層的數量可以不同)的感知機,並將一層感知機的輸出作為下一層的輸入,依次套娃下去。像圖中,下一層神經元的權重數量 = 上一層的神經元數量,稱為全連接,是神經網絡中常見的連接方式,本文也只考慮這種連接方式。
這裏的「輸入層」其實就是輸入的數據(是的,這一層不是神經元),類似之前的x0、x1、x2;「輸出層」就是用於輸出的神經元所組成的層,有了多個感知機,我們也可以得到多個輸出;夾在「輸入層」與「輸出層」之間的就叫「隱藏層」,因為在實際使用神經網絡時,就只是輸入一組數值作為「輸入層」,再看看「輸出層」得到的結果,並不關心中間的運算。
我們常説的「深度學習」裏的「深度」指的就是神經網絡中「隱藏層」的層數(只不過現在這個詞有點被炒作了),當一個神經網絡的隱藏層超過3層時,它就是「深度神經網絡」。
通過改變神經網絡的結構或者調節神經網絡的權重和偏置,我們可以用神經網絡近似任何的函數、甚至是一些摸不着頭腦的規律。
比如影響小明今天玩不玩網遊的因素有:今日作業量、心情、本月剩餘流量、今天是星期幾,但我們並不知道這些因素與小明玩不玩的具體數學關係,只能大概地推斷:今天小明作業多,不會玩遊戲;又或者今天是星期六,雖然作業還有很多,但他還是會玩遊戲……可一旦知道具體數學關係,我們就可以通過計算準確預測小明是否會玩遊戲,就像我們知道了牛頓力學公式,就可以根據物體的質量和被射出的力來計算它的運動軌跡一樣。
所以我們所關心的、實際所使用的都是這種已經設置好正確權重和偏置的神經網絡,像在與GPT聊天時怕「污染數據庫」這類事就不用操心了。
要如何為神經網絡的各個神經元的各個權重設置正確的值,使它能夠輸出我們預期的結果呢?手動調肯定不現實,所以我們會運用一些數學知識讓程序自行調整權重,這個過程就是「訓練/學習」。
我們會給出一些輸入以及該輸入所對應的正確輸出,比如我們可以記錄小明上個學期玩網遊時的各因素值以及不玩時的各因素值,這些作為「訓練集」。然後設計一個「損失函數」評判當前神經網絡的輸出與正確輸出之間的差距。而程序就是不斷地調節各個權重,使差距越來越小,這種調節的根據是「導數」,但在這裏我就不展開了。總之,如果訓練得當,神經網絡的損失就會越來越小,直到停在一個值附近,這就是「收斂」。
篇幅所限,我刻意沒有講相關的數學原理,如果你對此感興趣,又或者對MLP的運作仍有困惑,可以看看以下兩個視頻。如果準備好了,下面就進入代碼實現環節吧。
視頻1:
https://www.bilibili.com/video/BV1bx411M7Zx/?spm_id_from=333....
視頻2:
https://www.bilibili.com/video/BV1o64y1i7yw/?spm_id_from=333....
三、代碼實現
1. 相關數學
關於數學部分,我只進行簡要説明,不講它們的數學原理,也不過多註釋。如果你只是想將神經網絡應用到遊戲中,那這部分完全可以不必深究原理,弄清它們應用的場合即可。
a. 初始化權重函數
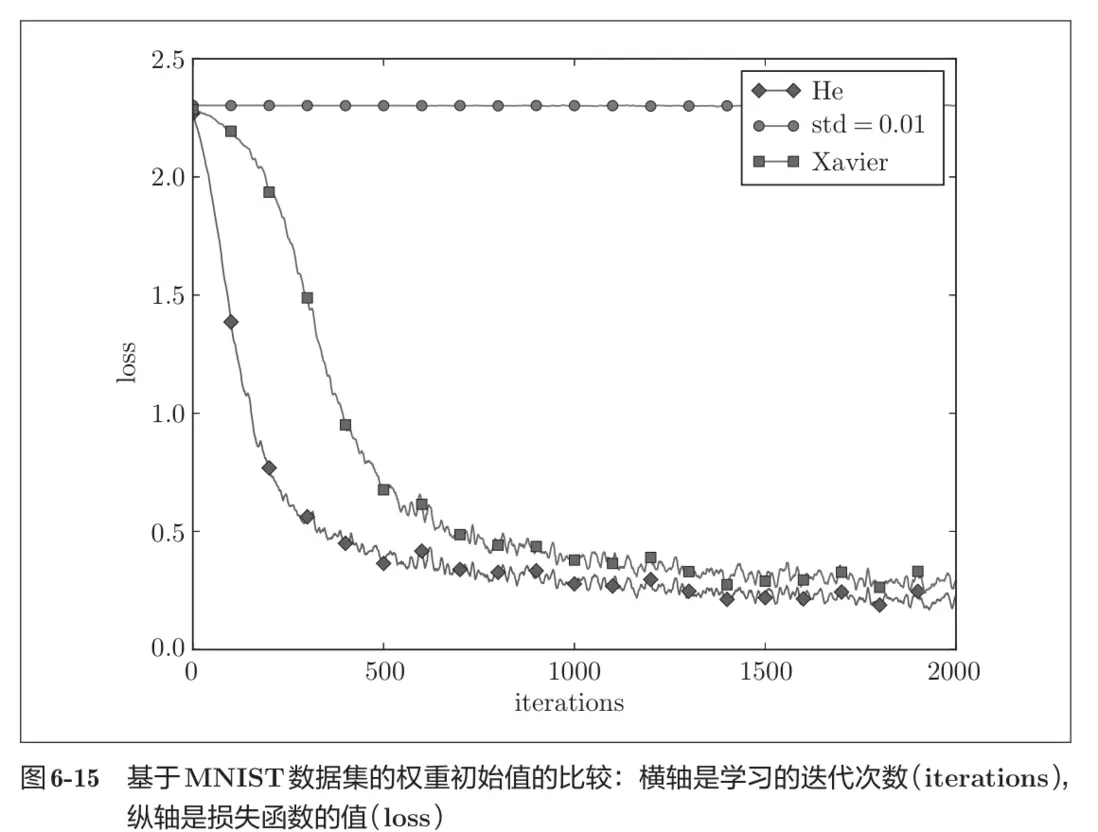
神經網絡權重的初始化十分重要,它會影響你的神經網絡最後能否訓練成功。這裏實現了3種典型的初始化方法:
- 隨機初始化(std = 0.01):是比較普通的方法,深度學習新手接觸的第一個初始化方式。
- Xavier初始化:適用於激活函數為Sigmoid和Tanh的場合。
- He初始化:適用於激活函數為ReLU及其衍生函數,如Leaky ReLU的場合。
這裏我還用了枚舉,方便在編輯時切換初始化的方法(後續幾類數學函數也會用這種方法):
using System;
namespaceJufGame.AI.ANN
{
publicstaticclassInitWFunc
{
publicenum Type
{
Random, Xavier, He, None
}
public static void InitWeights(Type initWFunc, Neuron neuron)
{
switch(initWFunc)
{
case Type.Xavier:
XavierInitWeights(neuron.Weights);
break;
case Type.He:
HeInitWeights(neuron.Weights);
break;
case Type.Random:
RandomInitWeights(neuron.Weights);
break;
default:
break;
}
}
private static void RandomInitWeights(float[] weightsList)
{
var rand = new Random();
for (int i = 0; i < weightsList.Length; ++i)
{
//使用較小的標準差,適合普通的隨機初始化
weightsList[i] = (float)(rand.NextGaussian() * 0.01);
}
}
private static void XavierInitWeights(float[] weightsList)
{
var rand = new Random();
var scale = 1f / MathF.Sqrt(weightsList.Length);
for (int i = 0; i < weightsList.Length; ++i)
{
weightsList[i] = (float)(rand.NextDouble() * 2 * scale - scale);
}
}
private static void HeInitWeights(float[] weightsList)
{
var rand = new Random();
var stdDev = MathF.Sqrt(2f / weightsList.Length); //計算標準差
for (int i = 0; i < weightsList.Length; ++i)
{
//生成服從正態分佈的隨機數,並乘以標準差
weightsList[i] = (float)(rand.NextGaussian() * stdDev);
}
}
// 用於生成服從標準正態分佈的隨機數的輔助方法
private static double NextGaussian(this Random rand)
{
double u1 = 1.0 - rand.NextDouble(); // 生成 [0, 1) 之間的隨機數
double u2 = 1.0 - rand.NextDouble();
// 使用 Box-Muller 變換生成正態分佈的隨機數
return Math.Sqrt(-2.0 * Math.Log(u1)) * Math.Sin(2.0 * Math.PI * u2);
}
}
}b. 激活函數
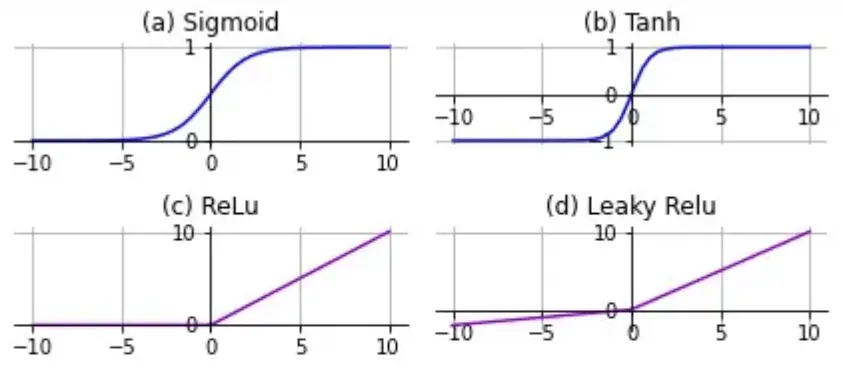
一般神經網絡中所有隱藏層都使用同一種激活函數,輸出層根據問題需求可能會使用和隱藏層不一樣的激活函數。激活函數都有非線性且可導的特點,我也實現了一些典型的激活函數:
- 直接輸出(Identify):不做處理直接輸出,用於輸出層。
- Sigmoid:早期的主流,現在一般用於輸出層需要將輸出值限制在0~1的場合,或者是隻有兩個輸出的二分問題。
- Tanh:相當於Sigmoid的改造,將輸出限制在了-1~1。
- ReLU:當今的主流激活函數,長得十分友好,甚至不用加減運算。一般選它準沒錯。
- Leaky ReLU:ReLU的改造,使得對負數輸入也有響應,但並沒有説它一定好於ReLU。如果你用ReLU訓練出現問題,可以換這個試試。
-
Softmax:把一系列輸出轉為總和為1的小數,並且維持彼此的大小關係,相當於把輸出結果轉為了概率。適用於多分類問題,但一定要搭配交叉熵損失函數使用。
using System; namespaceJufGame.AI.ANN { publicstaticclassActivationFunc { private delegate float FuncCalc(float x); privatestatic FuncCalc curAcFunc; publicenum Type { Identify, Softmax, Tanh, Sigmoid, ReLU, LeakyReLU } //按層使用激活函數計算 public static void Calc(Type funcType, Layer layer) { if(funcType == Type.Softmax) { Softmax_Calc(layer); } else { curAcFunc = funcType switch { Type.Sigmoid => Sigmoid_Calc, Type.Tanh => Tanh_Calc, Type.ReLU => ReLU_Calc, Type.LeakyReLU => LeakyReLU_Calc, _ => Identify_Calc, }; for(int i = 0; i < layer.Neurons.Length; ++i) { layer.Output[i] = curAcFunc(layer.Neurons[i].Sum); } } } //根據傳入下標index選取層中神經元,並進行求導 public static float Diff(Type funcType, Layer layer, int index) { return funcType switch { Type.Softmax => Softmax_Diff(layer, index), Type.Sigmoid => Sigmoid_Diff(layer, index), Type.Tanh => Tanh_Diff(layer, index), Type.ReLU => ReLU_Diff(layer, index), Type.LeakyReLU => LeakyReLU_Diff(layer, index), _ => Identify_Diff(), }; } #region 直接輸出 private static float Identify_Calc(float x) { return x; } private static float Identify_Diff() { return1; } #endregion #region Softmax private static void Softmax_Calc(Layer layer) { var neurons = layer.Neurons; var expSum = 0.0f; for(int i = 0; i < neurons.Length; ++i) { layer.Output[i] = MathF.Exp(neurons[i].Sum); expSum += layer.Output[i]; } for(int i = 0; i < neurons.Length; ++i) { layer.Output[i] /= expSum; } } private static float Softmax_Diff(Layer outLayer, int index) { return outLayer.Output[index] * (1 - outLayer.Output[index]); } #endregion #region Sigmoid private static float Sigmoid_Calc(float x) { return1.0f / (1.0f + MathF.Exp(-x)); } private static float Sigmoid_Diff(Layer outLayer, int index) { return outLayer.Output[index] * (1 - outLayer.Output[index]); } #endregion #region Tanh private static float Tanh_Calc(float x) { var expVal = MathF.Exp(-x); return (1.0f - expVal) / (1.0f + expVal); } private static float Tanh_Diff(Layer outLayer, int index) { return1.0f - MathF.Pow(outLayer.Output[index], 2.0f); } #endregion #region ReLU public static float ReLU_Calc(float x) { return x > 0 ? x : 0; } public static float ReLU_Diff(Layer outLayer, int index) { return outLayer.Neurons[index].Sum > 0 ? 1 : 0; } #endregion #region LeakyReLU private static float LeakyReLU_Calc(float x) { return x > 0 ? x : 0.01f * x; } private static float LeakyReLU_Diff(Layer outLayer, int index) { return outLayer.Neurons[index].Sum > 0 ? 1 : 0.01f; } #endregion } }
c. 更新權重函數
權重的更新涉及一些「超參數」,比如學習率、最大迭代次數等。這些參數是程序不會進行更新的,只能人工提前設置好。在神經網絡的學習中,學習率的值很重要,過小會導致訓練費時;過大則會導致學習發散而不能正確進行。但好在後麪人們想出來更好的權重更新函數,它們對「超參數」的依賴會減小很多。我們所實現的有:
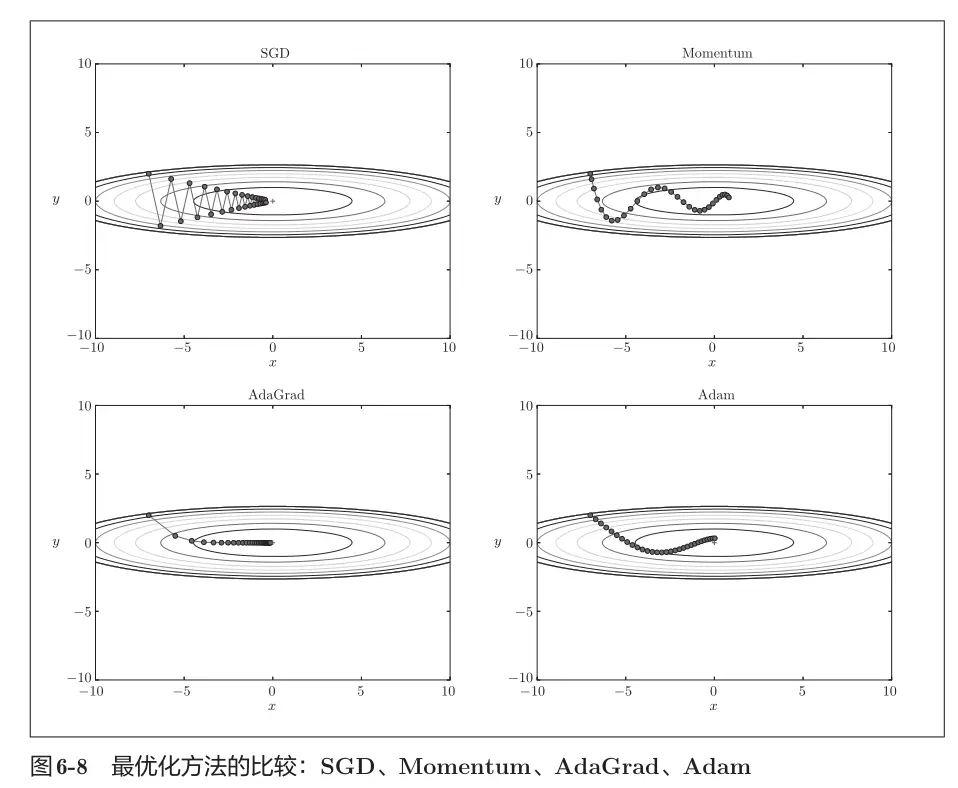
- SGD:隨機梯度下降,最簡單的一種更新方法,但有時並不是這麼高效,容易陷入局部最優解。
- Movement:基於物理上的動量概念,它會在更新權重的過程中考慮先前的更新步驟,需要為每個權重設置額外參數(用m表示)來記錄「動量」。
- AdaGrad:運用了學習率衰減的技巧,為每個權重適當地調整學習率,相當於給每個權重都設置了獨立的學習率,也需要額外參數(用v表示)記錄。
- Adam:將Movment與AdaGrad結合了起來,通過組合二者的優點,有望實現參數空間的高效搜索。
當然,上述4個方法各有優劣,可以優先考慮SGD和Adam。
順帶一提,權重的更新都是建立在「梯度」之上的,「梯度」可以理解為對神經網絡整體權重的變化趨勢。你想,有這麼多權重要更新,有時訓練一個樣本A後,會要求權重w0+ = 0.01、w1- = 0.05以減小誤差,但訓練下一個樣本B時,又要求w0- = 0.02、w1+ = 0.04,一個訓練集有這麼多樣本,要以哪個樣本訓練時產生的權重變化為準呢?
答案是累加每個樣本帶來的誤差並取平均值。如果覺得還不清楚,可以看看這個視頻:
https://www.bilibili.com/video/BV16x411V7Qg/?spm_id_from=333....
還有一點,偏置b也是隨着權重更新的,它可以視為一個輸入始終為1,權重為b的權重。在後續的實現中,我將偏置放在儲存權重的列表的最後一位。(但後來才知道不提倡這種寫法。)
using System;
namespaceJufGame.AI.ANN
{
publicstaticclassUpdateWFunc
{
privateconstfloat MinDelta = 1e-7f;
privateconstfloat beta1 = 0.9f;
privateconstfloat beta2 = 0.999f;
private delegate void UpdateLayer(Neuron curNeuron, float learningRate, int curEpochs, int samplesCount);
publicenum Type
{
SGD, Momentum, AdaGrad, Adam
}
public static void UpdateNetWeights(Type type, NeuralNet net, int samplesCount)
{
UpdateLayer updateLayerFunc = type switch
{
Type.Momentum => Momentum_UpdateW,
Type.AdaGrad => AdaGrad_UpdateW,
Type.Adam => Adam_UpdateW,
_ => SGD_UpdateW,
};
var curLayer = net.OutLayer;
for(int j = 0; j < curLayer.Neurons.Length; ++j)
{
updateLayerFunc(curLayer.Neurons[j], net.LearningRate, net.CurEpochs ,samplesCount);
}
for(int i = 0; i < net.HdnLayers.Length; ++i)
{
curLayer = net.HdnLayers[i];
for(int j = 0; j < curLayer.Neurons.Length; ++j)
{
updateLayerFunc(curLayer.Neurons[j], net.LearningRate, net.CurEpochs, samplesCount);
}
}
}
#region 各參數損失貢獻計算
//計算各參數對損失的貢獻程度(也是各參數的變化的值)
public static void CalcDelta(NeuralNet net, float[] input)
{
var lastInput = input;
for(int i = 0; i < net.HdnLayers.Length; ++i)
{
var curLayer = net.HdnLayers[i];
CalcLayerDelta(curLayer, lastInput);
lastInput = curLayer.Output;
}
CalcLayerDelta(net.OutLayer, lastInput);
}
private static void CalcLayerDelta(Layer curLayer, float[] lastInput)
{
for(int j = 0, k; j < curLayer.Neurons.Length; ++j)
{
var curNeuron = curLayer.Neurons[j];
for(k = 0; k < lastInput.Length; ++k)
{
//通過反向傳播時神經元的損失,計算每個權重的貢獻貢獻並累加
curNeuron.WeightParams["Delta"][k] += curNeuron.Params["Error"] * lastInput[k];
}
//同理計算偏置的損失貢獻
curNeuron.WeightParams["Delta"][k] += curNeuron.Params["Error"];
}
}
#endregion
#region SGD
private static void SGD_UpdateW(Neuron curNeuron, float learningRate, int curEpochs, int samplesCount)
{
for(int k = 0; k < curNeuron.Weights.Length; ++k)
{
var gradient = curNeuron.WeightParams["Delta"][k] / samplesCount;
curNeuron.Weights[k] -= learningRate * gradient;
curNeuron.WeightParams["Delta"][k] = 0;
}
}
#endregion
#region Momentum
private static void Momentum_UpdateW(Neuron curNeuron, float learningRate, int curEpochs, int samplesCount)
{
for(int k = 0; k < curNeuron.Weights.Length; ++k)
{
var gradient = curNeuron.WeightParams["Delta"][k] / samplesCount;
curNeuron.WeightParams["m"][k] = beta1 * curNeuron.WeightParams["m"][k] - learningRate * gradient;
curNeuron.Weights[k] += curNeuron.WeightParams["m"][k];
curNeuron.WeightParams["Delta"][k] = 0;
}
}
#endregion
#region AdaGrad
private static void AdaGrad_UpdateW(Neuron curNeuron, float learningRate, int curEpochs, int samplesCount)
{
for(int k = 0; k < curNeuron.Weights.Length; ++k)
{
var gradient = curNeuron.WeightParams["Delta"][k] / samplesCount;
curNeuron.WeightParams["v"][k] += gradient * gradient;
curNeuron.Weights[k] -= learningRate * gradient / MathF.Sqrt(curNeuron.WeightParams["v"][k] + MinDelta);
curNeuron.WeightParams["Delta"][k] = 0;
}
}
#endregion
#region Adam
private static void Adam_UpdateW(Neuron curNeuron, float learningRate, int curEpochs, int samplesCount)
{
for(int k = 0; k < curNeuron.Weights.Length; ++k)
{
var gradient = curNeuron.WeightParams["Delta"][k] / samplesCount;
curNeuron.WeightParams["m"][k] = beta1 * curNeuron.WeightParams["m"][k] + (1 - beta1) * gradient;
curNeuron.WeightParams["v"][k] = beta2 * curNeuron.WeightParams["v"][k] + (1 - beta2) * gradient * gradient;
var mHat = curNeuron.WeightParams["m"][k] / (1 - MathF.Pow(beta1, curEpochs));
var vHat = curNeuron.WeightParams["v"][k] / (1 - MathF.Pow(beta2, curEpochs));
curNeuron.Weights[k] -= learningRate * mHat / (MathF.Sqrt(vHat) + MinDelta);
curNeuron.WeightParams["Delta"][k] = 0;
}
}
#endregion
}
}d. 損失函數
損失函數用來衡量輸出與正確值之間的差距,這裏實現的是最常用的兩個損失函數:
- 均方差函數:簡單實用,形式如下:
- 交叉熵函數:主要用在多分類問題上,配合Softmax使用:
using System;
namespaceJufGame.AI.ANN
{
publicstaticclassLossFunc
{
privateconstfloat MinDelta = 1e-7f;
publicenum Type
{
MeanSqurad, CrossEntropy,
}
public static float Calc(Type type, float[] targetOut, Layer outLayer)
{
return type switch
{
Type.MeanSqurad => MeanSquradErr_Calc(targetOut, outLayer),
_ => CrossEntropy_Calc(targetOut, outLayer),
};
}
public static void Diff(Type type, float[] targetOut, Layer outLayer)
{
switch(type)
{
case Type.MeanSqurad:
MeanSquradErr_Diff(targetOut, outLayer);
break;
case Type.CrossEntropy:
CrossEntropy_Diff(targetOut, outLayer);
break;
};
}
private static float MeanSquradErr_Calc(float[] targetOut, Layer outLayer)
{
var errSum = 0.0f;
for(int i = 0; i < targetOut.Length; ++i)
{
errSum += MathF.Pow(outLayer.Output[i] - targetOut[i], 2);
}
return errSum / (2 * targetOut.Length);
}
private static void MeanSquradErr_Diff(float[] targetOut, Layer outLayer)
{
for(int i = 0; i < targetOut.Length; ++i)
{
var curNeuron = outLayer.Neurons[i];
curNeuron.Params["Error"] = outLayer.Output[i] - targetOut[i];
}
}
private static float CrossEntropy_Calc(float[] targetOut, Layer outLayer)
{
var errSum = 0.0f;
for(int i = 0; i < targetOut.Length; ++i)
{
//加上一個極小值再取log,放置出現log(0)報錯
errSum -= targetOut[i] * MathF.Log(outLayer.Output[i] + MinDelta);
}
return errSum;
}
private static void CrossEntropy_Diff(float[] targetOut, Layer outLayer)
{
for(int i = 0; i < targetOut.Length; ++i)
{
var curNeuron = outLayer.Neurons[i];
//用Output[i]的前提:神經網絡的輸出經過了softmax處理
curNeuron.Params["Error"] = outLayer.Output[i] - targetOut[i];
}
}
}
}2. 感知機(神經元)
簡單地對神經元結構進行實現,只是神經元在訓練時,需要為自身或者自身的權重記錄一些額外信息,所以多了WeightParams和Params備以記錄。
- 為什麼不記錄激活函數的計算結果out?
因為在訓練過程中常常要以層為單位統一處理激活函數的計算結果,故而將out都記錄在層中了。(實際上Python中許多深度學習框架庫都是以層為最小單位構建神經網絡的,這有利於進行矩陣運算,但在我們的實現中,一來沒用到矩陣運算,二來是希望能讓大家更直接地看到神經網絡訓練、計算的細節,所以我們以單個神經元作為最小的單位。) -
為什麼沒有激活函數f(x)?
因為我們之前説過,神經網絡的隱藏層都是使用同一種激活函數,頂多輸出層用的不太一樣。也就是説我們只需要記錄兩個函數的類型,所以讓後續實現的神經網絡類記下就行了,沒必要每個神經元都記錄,浪費空間。using System; using System.Collections.Generic; using UnityEngine; namespaceJufGame.AI.ANN { [Serializable] // 方便在編輯器頁面查看 publicclassNeuron { //神經元權重列表,末位放置偏置b publicfloat[] Weights => weights; //加權和 publicfloat Sum => sum; //為各個權重分配的額外參數 public Dictionary<string, float[]> WeightParams{ get; privateset; } //為神經元本身分配的額外參數 public Dictionary<string, float> Params{ get; privateset; } [SerializeField]privatefloat[] weights; privatefloat sum; public Neuron(int weightCount) { weights = newfloat[weightCount + 1];//末尾放偏置 } /// <summary> /// 初始化訓練所需參數列表,僅在訓練時調用 /// </summary> public void InitCache() { Params = new Dictionary<string, float> { ["Error"] = 0,//該值用來記錄,每次更新時的累計損失 }; WeightParams = new Dictionary<string, float[]> { //記錄權重待變化值 ["Delta"] = newfloat[weights.Length], //Momentum和Adam中,用於記錄權重變化的「動量」 ["m"] = newfloat[weights.Length], //AdaGrad和Adam中,用於記錄權重獨立學習率 ["v"] = newfloat[weights.Length], }; } //計算Sum public float CalcSum(float[] input) { int i; sum = 0; for(i = 0; i < input.Length; ++i) { sum += weights[i] * input[i];//加權和 } sum += weights[i];//加上權重 return Sum; } } }
3. 層
沒有太多必要説的,就是嵌套調用了包含的各神經元的函數,比如層的計算就是各個神經元的計算,其它同理。
using System;
using UnityEngine;
namespaceJufGame.AI.ANN
{
[Serializable]
publicclassLayer
{
public Neuron[] Neurons => neurons;//存儲神經元
publicfloat[] Output => output;//存儲各神經元激活函數輸出
[SerializeField] private Neuron[] neurons;
[SerializeField] privatefloat[] output;
public Layer(int neuronCount)
{
output = newfloat[neuronCount];
neurons = new Neuron[neuronCount];
}
//對層中的每個神經元的權重進行初始化
public void InitWeights(int weightCount, InitWFunc.Type initType)
{
for(int i = 0; i < neurons.Length; ++i)
{
neurons[i] = new Neuron(weightCount);
InitWFunc.InitWeights(initType, neurons[i]);
}
}
//初始化層中每個神經元的額外參數
public void InitCache()
{
for(int i = 0; i < neurons.Length; ++i)
{
neurons[i].InitCache();
}
}
//計算該層,實際上就是計算所有神經元的加權和,並求出激活函數的輸出
public float[] CalcLayer(float[] inputData, ActivationFunc.Type acFuc)
{
for(int i = 0; i < neurons.Length; ++i)
{
neurons[i].CalcSum(inputData);
}
ActivationFunc.Calc(acFuc, this);
return output;
}
}
}4. 多層感知機(神經網絡)
神經網絡也一樣,是對層的各個功能的再度包裝,只是多了些超參數成員變量。
- 為什麼沒有輸入層?
因為輸入層其實就只是輸入的數值,沒必要單獨設置一個層(Python中許多深度學習框架也是這樣的)。 -
怎麼讀取輸出?
直接讀取輸出層的輸出列表即可。using System; using UnityEngine; namespaceJufGame.AI.ANN { [Serializable] publicclassNeuralNet { publicfloat TargetError = 0.0001f;//預期誤差,當損失函數的結果小於它時,就停止訓練 publicfloat LearningRate = 0.01f;//學習率 publicint CurEpochs;//記錄當前迭代的次數 public ActivationFunc.Type hdnAcFunc;//隱藏層激活函數類型 public ActivationFunc.Type outAcFunc;//輸出層激活函數類型 public Layer[] HdnLayers => hdnLayers;//隱藏層 public Layer OutLayer => outLayer;//輸出層 [SerializeField] private Layer[] hdnLayers; [SerializeField] private Layer outLayer; public NeuralNet(int hdnLayerCount, int[] neuronsOfLayers, int outCount, ActivationFunc.Type hdnAcFnc, ActivationFunc.Type outAcFnc, float targetError = 0.0001f, float learningRate = 0.01f) { outLayer = new Layer(outCount); hdnLayers = new Layer[hdnLayerCount]; for(int i = 0, j = 0; i < hdnLayerCount; ++i) { hdnLayers[i] = new Layer(neuronsOfLayers[j]); } hdnAcFunc = hdnAcFnc; outAcFunc = outAcFnc; TargetError = targetError; LearningRate = learningRate; } //初始化各神經元權重 public void InitWeights(int inputDataCount, InitWFunc.Type initType) { int neuronNum = inputDataCount; for(int i = 0; i < HdnLayers.Length; ++i) { hdnLayers[i].InitWeights(neuronNum, initType); neuronNum = HdnLayers[i].Neurons.Length; } outLayer.InitWeights(neuronNum, initType); } //初始化各神經元額外參數列表 public void InitCache() { for(int i = 0; i < HdnLayers.Length; ++i) { hdnLayers[i].InitCache(); } outLayer.InitCache(); } //計算神經網絡 public float[] CalcNet(float[] inputData) { var curInput = inputData; for(int j = 0; j < hdnLayers.Length; ++j) { curInput = hdnLayers[j].CalcLayer(curInput, hdnAcFunc); } return outLayer.CalcLayer(curInput, outAcFunc); } } }至此,神經網絡就搭建完成了,並沒有想象的那麼複雜。
5. 訓練器
先實現一個訓練器的基類……等等,明明就一種神經網絡,為什麼還要有基類,直接寫不好嗎?
其實最初是打算實現多種神經網絡的,但後來考試臨近,不得不轉移重心,最終只實現了最簡單的MLP。Unity本身也已經可以導入ONNX模型,如果要在遊戲裏想實現圖像識別這類複雜功能的話,導入模型似乎更方便,所以實現更多神經網絡的必要性就值得考慮了。當然,這些文末會再進行討論。
先來看看這個基類有哪些東西:
using UnityEngine;
namespaceJufGame.AI.ANN
{
publicabstractclassTraining
{
public NeuralNet TrainingNet;//需要訓練的神經網絡
publicfloat[][] InputSet => inputSet;//訓練輸入集
/*沒有「訓練輸出集」是因為並非所有類型的神經網絡都需要「訓練輸出」
所以它不是基類必需的,當然,這些就是題外話了*/
protectedfloat[][] inputSet;
[SerializeField] protectedint maxEpochs;//最大迭代次數
public Training(NeuralNet initedNet, int maxEpochs)
{
this.maxEpochs = maxEpochs;
TrainingNet = initedNet;
}
public void SetInput(float[][] inputSet)//設置訓練輸入集
{
this.inputSet = inputSet;
}
public abstract bool IsTrainEnd();//是否訓練完成
public abstract void Train(); //不斷訓練神經網絡
public abstract void Train_OneTime();//訓練(迭代)一次神經網絡
//打印神經網絡輸出的結果,調試用的
public static void DebugNetRes(NeuralNet net, float[][] testInput)
{
for(int i = 0; i < testInput.GetLength(0); ++i)
{
var res = net.CalcNet(testInput[i]);
for(int j = 0; j < res.Length; ++j)
{
Debug.Log("檢驗結果 " + i + " = " + res[j]);
}
}
}
}
}最後,就是真正用來訓練的類了,我們將採用最常見梯度下降法進行訓練。其中涉及前向傳播和反向傳播,我稍作解釋:
- 前向傳播(Forward Propagation):傳入訓練輸入樣本計算出當前神經網絡模型的輸出,並進一步計算損失(損失函數的計算結果其實在反向傳播中並沒有用,只是給開發者看的,用來判斷當前訓練情況)。
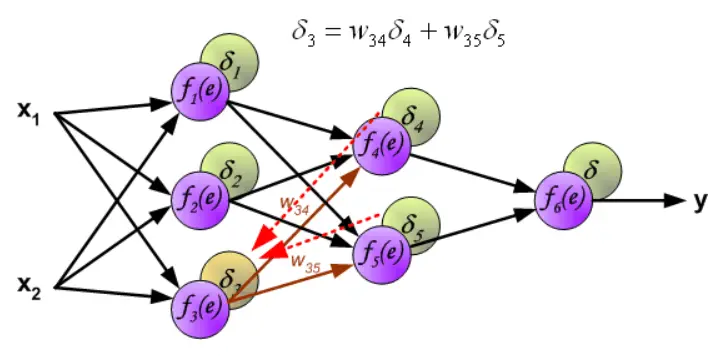
- 反向傳播(Backward Propagation):從損失函數開始,用鏈式求導法則,反向(輸出層➡隱藏層➡輸入層)計算每個神經元的損失(下圖中的δ、代碼中的Params["Error"])。通過神經元的損失,可以計算出神經元的每個參數(權重、偏置)的損失貢獻(權重更新函數代碼中的WeightParams["Delta"])並一直累加,直到訓練集被讀取完。這時,我們就説完成了一次訓練迭代。
完成一次迭代後(不是訓練完一個樣本後),將累加的損失除以訓練樣本數取得均值,再用權重更新函數對各參數進行更新。
這一迭代過程反覆進行,直到損失函數計算的誤差達到可容許範圍(也就是小於預期損失)或達到最大訓練次數,詳情可看《解讀反向傳播算法(圖與公式結合)》[1](但注意!該文章為了方便講解,訓練完一個樣本就開始更新權重了),實現如下:
using UnityEngine;
namespaceJufGame.AI.ANN
{
[System.Serializable]
publicclassBPNN : Training
{
publicfloat[][] OutputSet => outputSet;
[SerializeField] privatefloat meanError = float.MaxValue;
[SerializeField] private LossFunc.Type errorFunc;
[SerializeField] private UpdateWFunc.Type updateWFunc;
privatefloat[][] outputSet;
public BPNN(NeuralNet initedNet, LossFunc.Type errorFunc, UpdateWFunc.Type updateWFunc, int maxEpochs): base(initedNet,maxEpochs)
{
this.errorFunc = errorFunc;
this.updateWFunc = updateWFunc;
}
public void SetOutput(float[][] outputSet)
{
this.outputSet = outputSet;
}
public override bool IsTrainEnd()//判斷是否訓練完成
{
return meanError < TrainingNet.TargetError
|| maxEpochs < TrainingNet.CurEpochs;
}
public override void Train()
{
meanError = float.MaxValue;
while(!IsTrainEnd())
{
Train_OneTime();
}
}
public override void Train_OneTime()
{
int samplesCount = inputSet.GetLength(0);//記下樣本數量
++TrainingNet.CurEpochs;//更新迭代次數
meanError = 0;
for(int i = 0; i < samplesCount; ++i)
{
ForWard(i);
Backpropagation();
UpdateWFunc.CalcDelta(TrainingNet, inputSet[i]);
}
UpdateWFunc.UpdateNetWeights( updateWFunc, TrainingNet, samplesCount);
meanError /= samplesCount;//取樣本誤差均值作為本次迭代的誤差
#if UNITY_EDITOR
Debug.Log($"誤差:{meanError}");//調試時用的
#endif
}
private void ForWard(int trainIndex)
{
var outLayer = TrainingNet.OutLayer;
TrainingNet.CalcNet(inputSet[trainIndex]);
meanError = LossFunc.Calc(errorFunc, outputSet[trainIndex], outLayer);
/*這裏圖省事,將反向傳播的第一步一併計算了*/
LossFunc.Diff(errorFunc, outputSet[trainIndex], outLayer);//損失函數求導
for(int i = 0; i < outLayer.Neurons.Length; ++i)//輸出層激活函數求導
{
outLayer.Neurons[i].Params["Error"] *= ActivationFunc.Diff(TrainingNet.outAcFunc, outLayer, i);
}
}
private void Backpropagation()
{
var lastLayer = TrainingNet.OutLayer;
for(int i = TrainingNet.HdnLayers.Length - 1; i > -1; --i)
{
var curLayer = TrainingNet.HdnLayers[i];
for(int j = 0; j < curLayer.Neurons.Length; ++j)
{
var curNeuron = curLayer.Neurons[j];
//每次計算損失時要清零,避免上次迭代結果產生的干擾
curNeuron.Params["Error"] = 0;
for(int k = 0; k < lastLayer.Neurons.Length; ++k)
{
var lastNeuron = lastLayer.Neurons[k];
curNeuron.Params["Error"] += lastNeuron.Params["Error"] * lastNeuron.Weights[j];
}
curNeuron.Params["Error"] *= ActivationFunc.Diff(TrainingNet.hdnAcFunc, curLayer, j);
}
lastLayer = curLayer;
}
}
}
}四、使用教程
一切都準備就緒了,那要怎麼運轉這個神經網絡呢?我們創建一個繼承了MonoBehavior的腳本,並聲明下面三個公開的字段:
using UnityEngine;
using JufGame.AI.ANN;
public class TrainANN : MonoBehaviour
{
public int inputCount;
public BPNN bp;
public InitWFunc.Type initW;
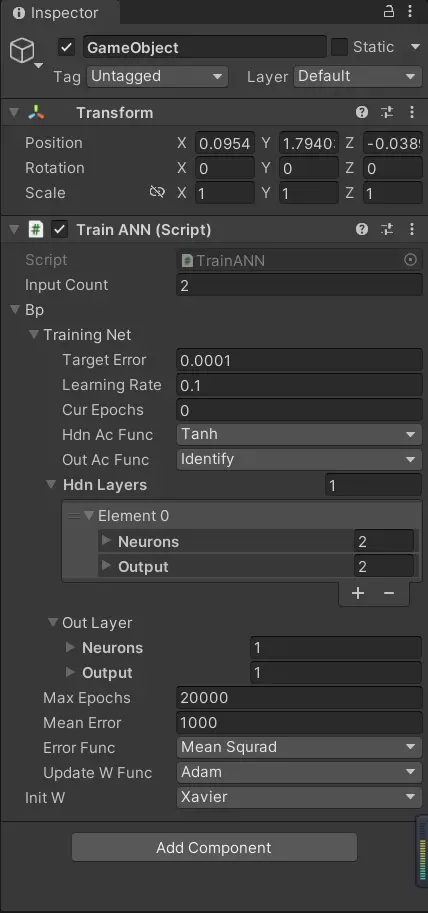
}將它掛載在場景的任一物體上,不出意外的話,你可以在編輯器看到神經網絡類的許多關鍵變量都可以顯示出來(如果你的沒有,就要注意是否遺漏[System.Serializable]或設置成了私有類):
我們再完善下腳本,設置好訓練輸入和輸出(以「異或」運算為例),使得神經網絡能在Unity運行時逐幀訓練:
public classTrainANN : MonoBehaviour
{
publicint inputCount;
public BPNN bp;
public InitWFunc.Type initW;
privatefloat[][] inSet = //異或運算的輸入
{
newfloat[]{1, 0},
newfloat[]{1, 1},
newfloat[]{0, 0},
newfloat[]{0, 1},
};
privatefloat[][] outSet = //異或運算的輸出
{
newfloat[]{1},
newfloat[]{0},
newfloat[]{0},
newfloat[]{1},
};
private void Awake()
{
bp.SetInput(inSet);//為訓練器設置訓練輸入集
bp.SetOutput(outSet);//為訓練器設置訓練輸出集
}
private void Start()
{
bp.TrainingNet.InitWeights(inputCount, initW);//初始化權重
bp.TrainingNet.InitCache();//初始化額外參數存儲
}
private void Update()
{
if(bp.IsTrainEnd())//如果訓練結束,就打印訓練完成的神經網絡 對訓練輸入集輸出
{
Training.DebugNetRes(bp.TrainingNet, inSet);
return;
}
bp.Train_OneTime();//沒有訓練結束,就每幀訓練一次
}
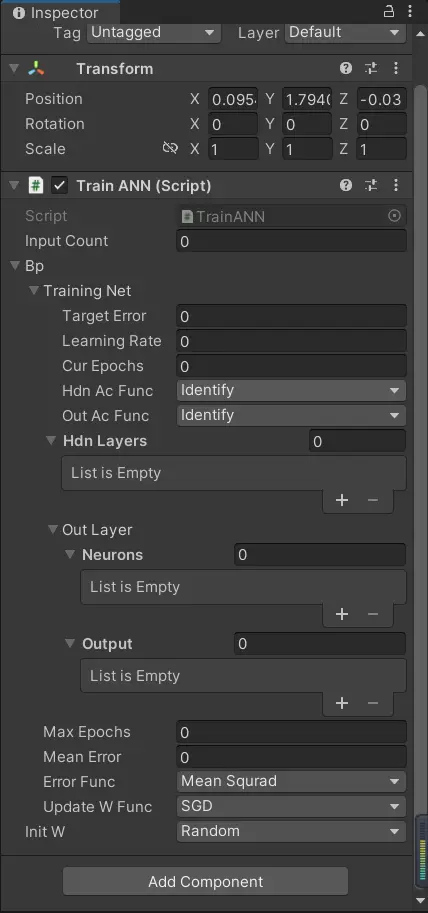
}回到編輯頁面,由於關鍵變量都可以直接修改,所以我們無需調用構造函數進行初始化。我們設置好它的預期誤差、最大迭代數等,可以參照下面這個設置:
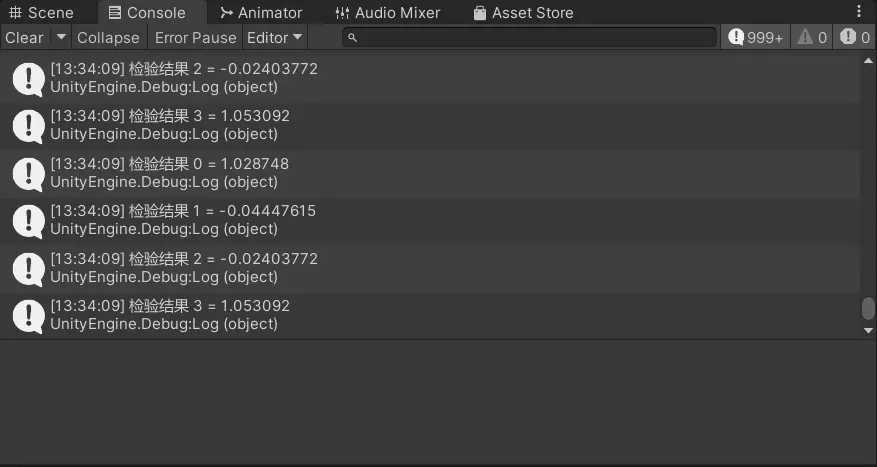
然後我們開始運行,不出意外的話,訓練很快就結束了(大概只花了100多次迭代),你也可以看到Console面板打印了神經網絡的輸出結果:
可以看到,結果是很接近真實值的(把預期誤差設小點還可以更接近),這也説明我們的訓練是奏效的!
- 可能在嘗試其它參數時(尤其是激活函數),會發現有時誤差會「停」在某個值下不去了,是怎麼回事?
這是陷入了局部最優解的情況,又或者是神經網絡幾乎停止訓練,在使用較少數據並且激活函數為ReLU的場合可能會出現。可以嘗試其它激活函數,或增加訓練樣本。
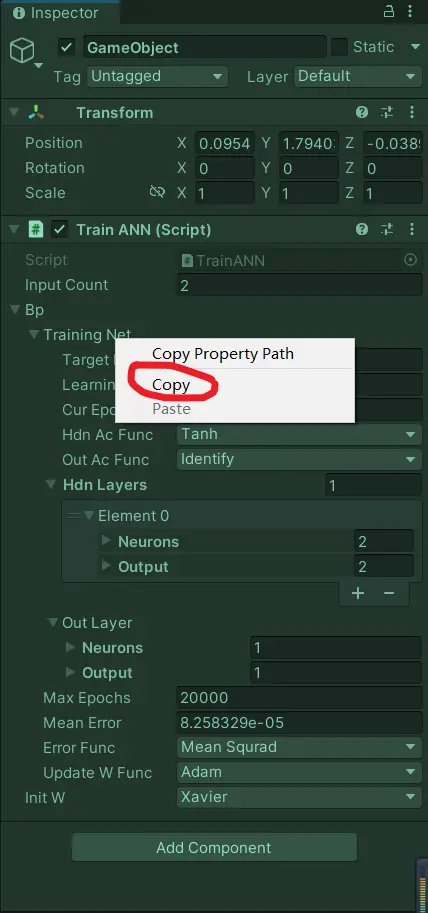
可一旦結束Unity運行後,編輯頁面這些被訓練好的參數就又變回去了,這該怎麼辦?很簡單,一旦訓練完後,就暫停運行(是暫停,不是結束),右鍵神經網絡的名字,將它複製下來。
創建一個新的腳本並將它掛在場景中,用以測試被複制的神經網絡能否正常工作:
using System.Collections;
using System.Collections.Generic;
using JufGame.AI.ANN;
using UnityEngine;
publicclassUseMLP : MonoBehaviour
{
public NeuralNet net;
privatefloat[][] inSet = //異或運算的輸入
{
newfloat[]{1, 0},
newfloat[]{1, 1},
newfloat[]{0, 0},
newfloat[]{0, 1},
};
private void Awake()
{
Training.DebugNetRes(net, inSet);
}
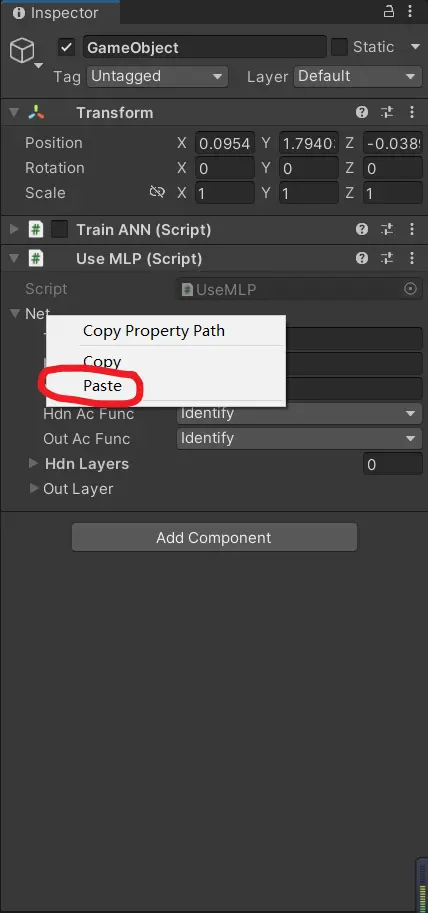
}將之前訓練好的神經網絡,粘貼給它,然後運行Unity:
不出意外的話,可以看到,這個神經網絡的輸出是十分正確的(我就不貼圖了)!
五、項目鏈接
最後一步,神經網絡要如何用在AI的行為決策中呢?
- 確定好AI決策相關的數據、並將其作為神經網絡的輸入。
比如生命值、攻擊力、與敵人之間的距離等,並將它們進行歸一化處理,比如一個角色生命值上限為100,現在生命值為50,那在將生命值作為輸入時不是傳入5,而是50/100 =0.5。總之,要將輸入的數據限制在0~1。這有利於神經網絡訓練,也能更正確地表達數據的信息,還是以剛才這個角色為例,假設他的魔法值上限為50,當前魔法值為40,能因為當前生命值50 > 當前魔法值40而認為當前角色更需要補充魔法值嗎?這顯然是不合理的。 - 根據輸入樣本擬定對應的輸出結果作為訓練輸出。
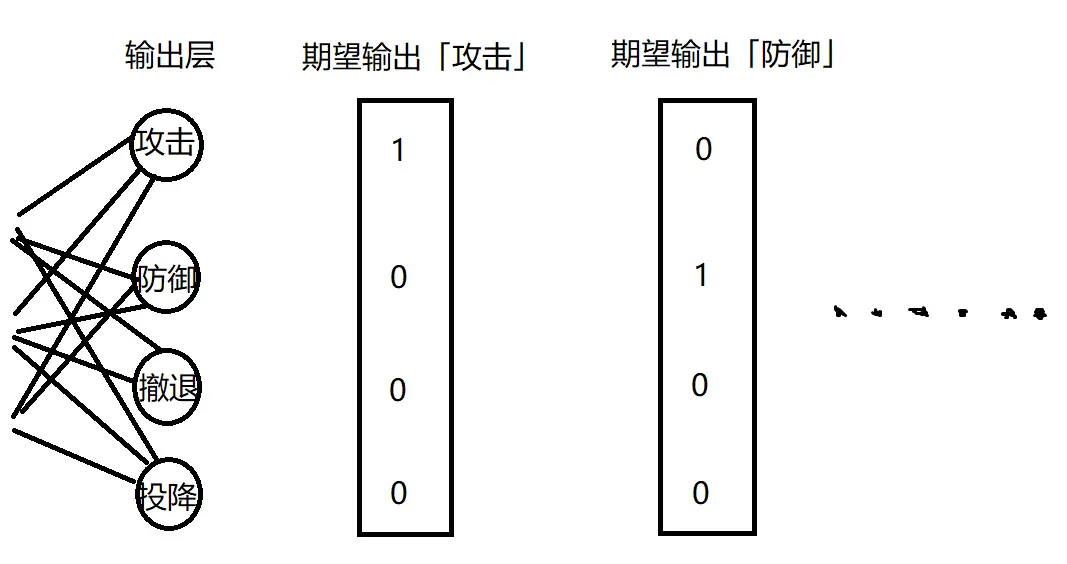
選取並想好了數據的歸一化處理後,我們需要擬定一部分輸入和輸出。設計訓練輸入還是比較簡單的,但輸出怎麼量化呢?因為決策要做的可是一個行為!我們可以這麼做,將輸出設置為執行某個行為的概率:
這樣一來,我們只要遍歷訓練完的神經網絡的所有輸出,選出值最大的那個神經元對應的行為來執行就可以了。
我所提供的項目[2]也是這樣做的,在項目中我用神經網絡控制了小機器人的三個行為:攻擊、防禦、奔跑。影響因素有自身生命值、敵方生命值、敵我間距。預期的結果就是當我方血少又離得很近(手動拖拽二者距離)時,機器人會防禦;當我方與對方旗鼓相當或更優勢時,機器人會攻擊,其餘情況會奔跑。總之,也是很簡單的行為。
六、尾聲
最後,我們再談談之前遺留的問題:是否有必要使用C# 構建神經網絡?我個人覺得,除了用來做這種決策行動,其它情況大可不必費力構建。主要原因在於:Unity可以導入由Python深度學習框架訓練出來的神經網絡模型,省時省力、效果還好。
不過,作為行為決策這種與遊戲邏輯緊密聯繫的部分,用遊戲引擎的腳本語言編寫是合適的。這方便觀察現象時時調整,也能更好地與其它遊戲腳本結合,而且行為決策所需的神經網絡複雜度並不大,因此帶來的性能影響並不大。
以《最高指揮官2》中使用的MLP為例:它的輸入層有34個神經元,隱藏層有98個神經元,輸出層有15個神經元,但它的計算不超過0.03毫秒。這顯然是個可以接受的結果。(該數據來源於2015版《遊戲人工智能》——第30章)
但是,神經網絡比起傳統的決策算法,最大的弊端是不方便調試以及最終效果的不可控。畢竟它的訓練是個純數學的過程,很難像以往那樣在程序中打斷點跟蹤;最終效果的不可控也導致可能要訓練多次才能得出較滿意的模型。所以在《最高指揮官2》中神經網絡也不是全權控制AI決策,而是搭配有限狀態機使用。還有一點就是需要準備大量的訓練數據,其實這並非是一定的,如果你能用好Excel導入數據或者是像《最高指揮官2》那樣使用適應度函數來代替具體的訓練樣本(篇幅所限,不展開了),感興趣的同學可以去了解下。
無庸置疑的是,這種AI決策方法的確會使角色更加生動,而且需要額外編寫的代碼也並不多,只是要多花些時間訓練。
參考:
[1] 解讀反向傳播算法(圖與公式結合)
https://zhuanlan.zhihu.com/p/96046514
[2] 提供的項目
https://www.alipan.com/s/P1Ve6cQYc1f
這是侑虎科技第1902篇文章,感謝作者狐王駕虎供稿。歡迎轉發分享,未經作者授權請勿轉載。如果您有任何獨到的見解或者發現也歡迎聯繫我們,一起探討。(QQ羣:793972859)
作者主頁:https://home.cnblogs.com/u/OwlCat
再次感謝狐王駕虎的分享,如果您有任何獨到的見解或者發現也歡迎聯繫我們,一起探討。(QQ羣:793972859)