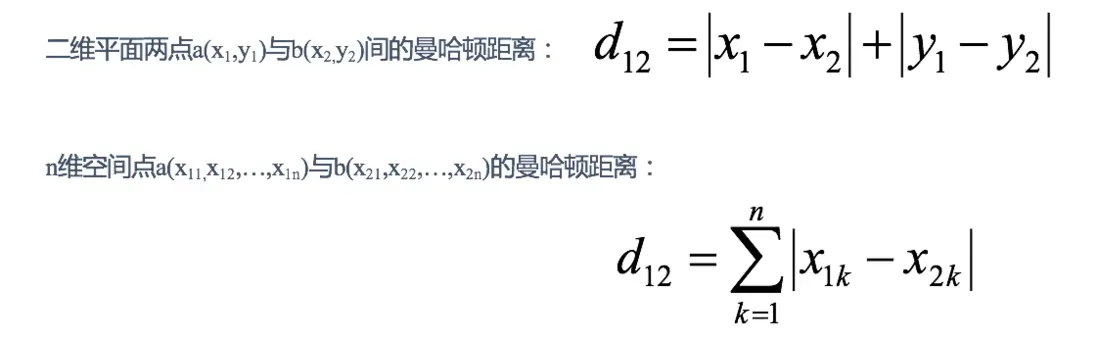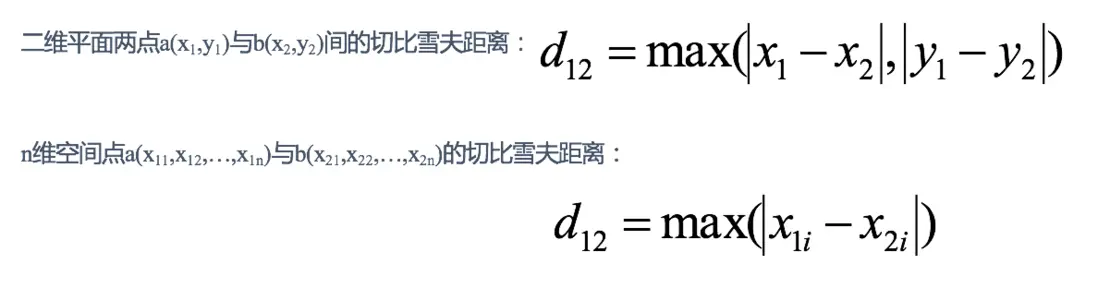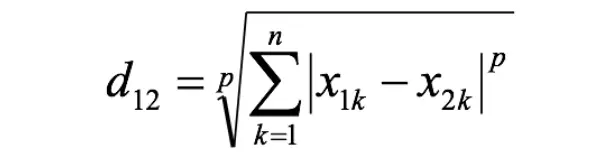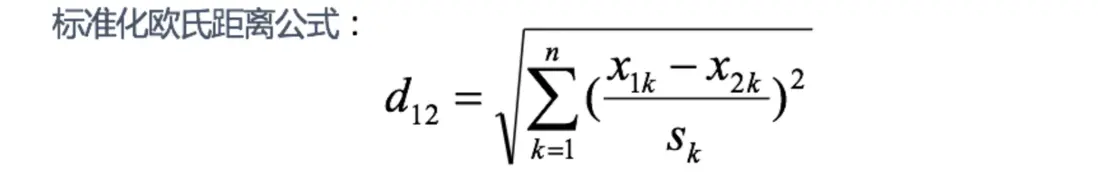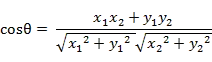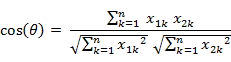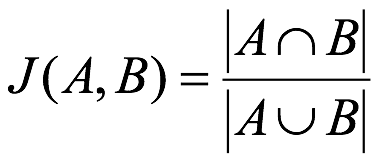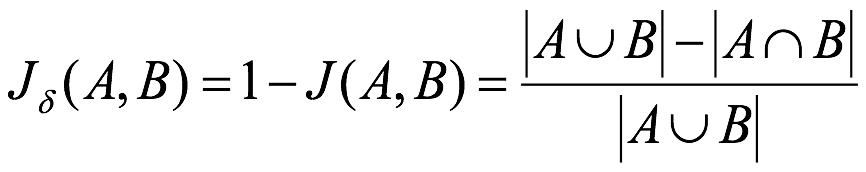🏆🏆🏆教程全知識點簡介:1.定位、目標。2. K-近鄰算法涵蓋距離度量、k值選擇、kd樹、鳶尾花種類預測數據集介紹、練一練、交叉驗證網格搜索、facebook簽到位置預測案例。3. 線性迴歸包括線性迴歸簡介、線性迴歸損失和優化、梯度下降法介紹、波士頓房價預測案例、欠擬合和過擬合、正則化線性模型、正規方程推導方式、梯度下降法算法比較優化、維災難。4. 邏輯迴歸涵蓋邏輯迴歸介紹、癌症分類預測案例(良惡性乳腺癌腫瘤預測、獲取數據)、ROC曲線繪製。5. 樸素貝葉斯算法包括樸素貝葉斯算法簡介、概率基礎複習、產品評論情感分析案例(取出內容列數據分析、判定評判標準好評差評)。6. 支持向量機涵蓋SVM算法原理、SVM損失函數、數字識別器案例。7. 決策樹算法包括決策樹分類原理、cart剪枝、特徵工程特徵提取、決策樹算法api、泰坦尼克號乘客生存預測案例。8. EM算法涵蓋初識EM算法、EM算法介紹。9. HMM模型包括馬爾科夫鏈、HMM簡介、前向後向算法評估觀察序列概率、維特比算法解碼隱藏狀態序列、HMM模型API介紹。10. 集成學習進階涵蓋Bagging、xgboost算法原理、otto案例(Otto Group Product Classification Challenge xgboost實現)、數據變化可視化、lightGBM、stacking算法基本思想、住房月租金預測。11. 聚類算法包括聚類算法api初步使用、聚類算法實現流程、模型評估、算法優化、特徵降維、用户對物品類別喜好細分案例、算法選擇指導。12. 數學基礎涵蓋向量與矩陣範數、朗格朗日乘子法、Huber Loss、極大似然函數取對數原因。

📚📚倉庫code.zip 👉直接-->: https://gitee.com/yinuo112/AI/blob/master/機器學習/嘿馬機器學... 🍅🍅
<!-- end:bj1 -->
✨ 本教程項目亮點
🧠 知識體系完整:覆蓋從基礎原理、核心方法到高階應用的全流程內容
💻 全技術鏈覆蓋:完整前後端技術棧,涵蓋開發必備技能
🚀 從零到實戰:適合 0 基礎入門到提升,循序漸進掌握核心能力
📚 豐富文檔與代碼示例:涵蓋多種場景,可運行、可複用
🛠 工作與學習雙參考:不僅適合系統化學習,更可作為日常開發中的查閲手冊
🧩 模塊化知識結構:按知識點分章節,便於快速定位和複習
📈 長期可用的技術積累:不止一次學習,而是能伴隨工作與項目長期參考
🎯🎯🎯全教程總章節
🚀🚀🚀本篇主要內容
機器學習算法定位、目標
定位
- 以算法、案例為驅動的學習,伴隨淺顯易懂的數學知識
- 作為人工智能領域的提升,掌握更深更有效的解決問題技能
目標
- 掌握機器學習常見算法原理
- 應用Scikit-learn實現機器學習算法的應用,
- 結合場景解決實際問題
1.1 K-近鄰算法簡介
學習目標
-
目標
- 瞭解什麼是KNN算法
- 知道KNN算法求解過程
1 什麼是K-近鄰算法
- 根據你的“鄰居”來推斷出你的類別
1.1 K-近鄰算法(KNN)概念
K Nearest Neighbor算法又叫KNN算法,這個算法是機器學習裏面一個比較經典的算法, 總體來説KNN算法是相對比較容易理解的算法
- 定義
如果一個樣本在特徵空間中的k個最相似(即特徵空間中最鄰近)的樣本中的大多數屬於某一個類別,則該樣本也屬於這個類別。
來源:KNN算法最早是由Cover和Hart提出的一種分類算法
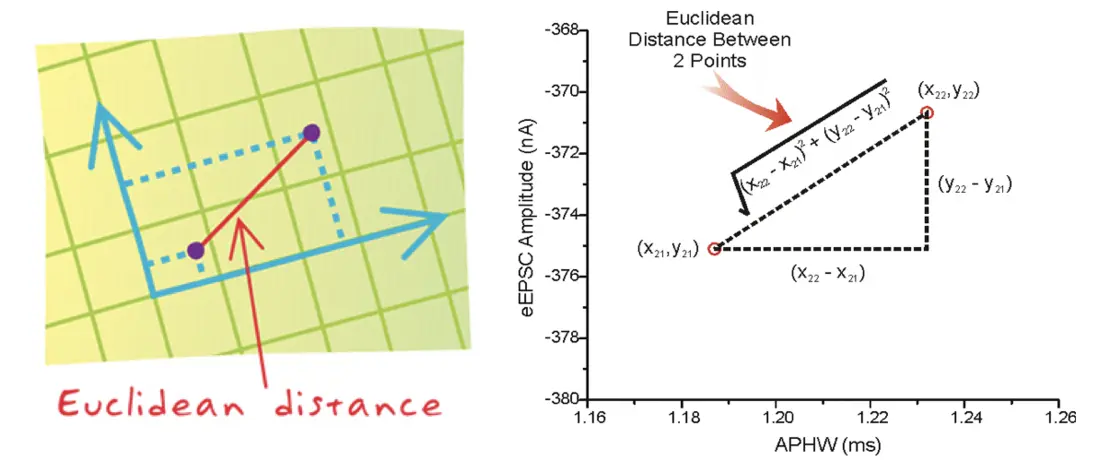
- 距離公式
兩個樣本的距離可以通過如下公式計算,又叫歐式距離 ,關於距離公式會在後面進行討論
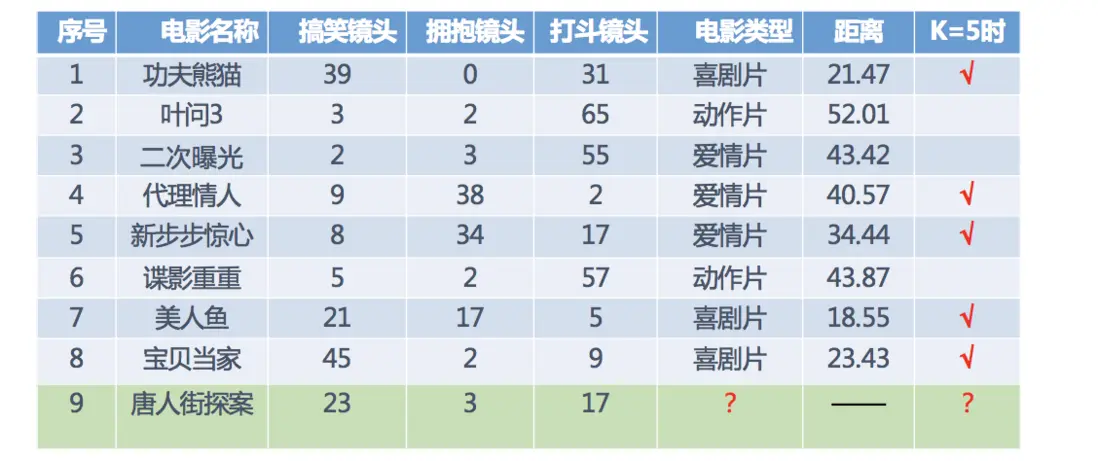
1.2 電影類型分析
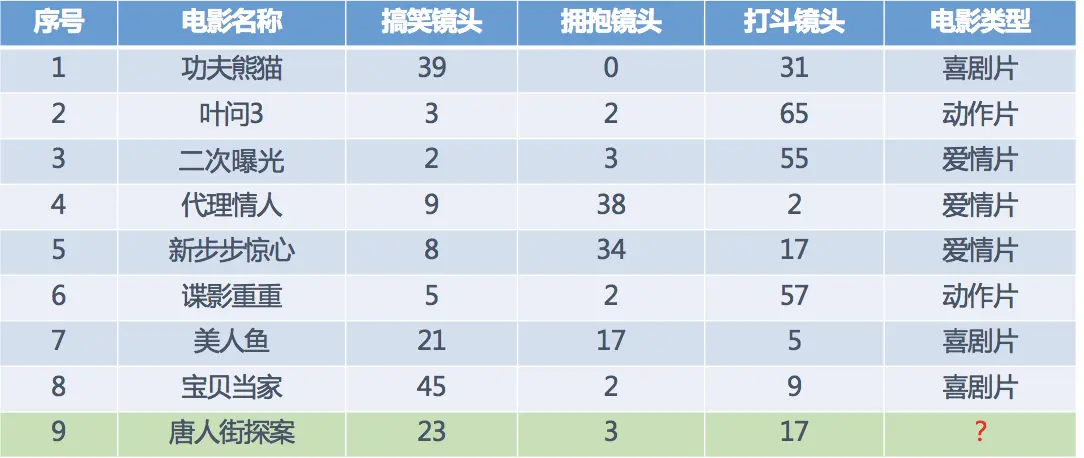
假設 現在有幾部電影
其中? 號電影不知道類別,如何去預測? 可以利用K近鄰算法的思想
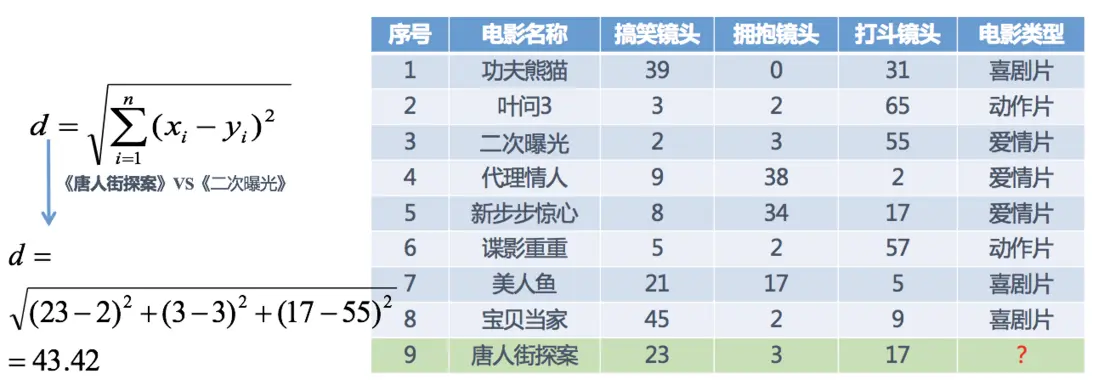
分別計算每個電影和被預測電影的距離,然後求解
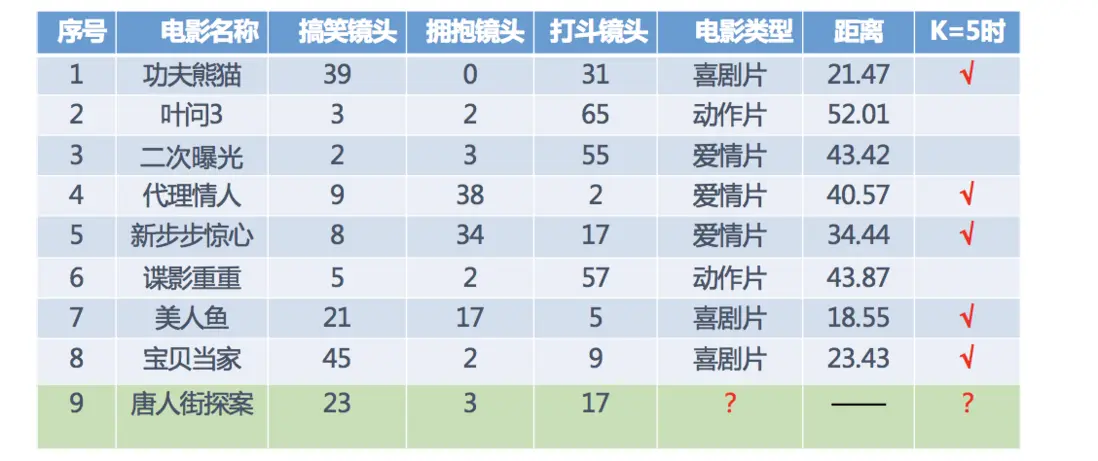
1.3 KNN算法流程總結
1)計算已知類別數據集中的點與當前點之間的距離
2)按距離遞增次序排序
3)選取與當前點距離最小的k個點
4)統計前k個點所在的類別出現的頻率
5)返回前k個點出現頻率最高的類別作為當前點的預測分類
2 小結
-
K-近鄰算法簡介【瞭解】
- 定義:就是通過你的"鄰居"來判斷你屬於哪個類別
- 如何計算你到你的"鄰居"的距離:一般時候,都是使用歐氏距離
1.2 k近鄰算法api初步使用
學習目標
-
目標
- 瞭解sklearn工具的優點和包含內容
- 應用sklearn中的api實現KNN算法的簡單使用
- 機器學習流程複習:
- 1.獲取數據集
- 2.數據基本處理
- 3.特徵工程
- 4.機器學習
- 5.模型評估
1 Scikit-learn工具介紹
- Python語言的機器學習工具
- Scikit-learn包括許多知名的機器學習算法的實現
- Scikit-learn文檔完善,容易上手,豐富的API
- 目前穩定版本0.19.1
1.1 安裝
pip3 install scikit-learn==0.19.1安裝好之後可以通過以下命令查看是否安裝成功
import sklearn- 注:安裝scikit-learn需要Numpy, Scipy等庫
1.2 Scikit-learn包含的內容
- 分類、聚類、迴歸
- 特徵工程
- 模型選擇、調優
2 K-近鄰算法API
-
sklearn.neighbors.KNeighborsClassifier(n_neighbors=5)
- n_neighbors:int,可選(默認= 5),k_neighbors查詢默認使用的鄰居數
3 案例
3.1 步驟分析
- 1.獲取數據集
- 2.數據基本處理(該案例中省略)
- 3.特徵工程(該案例中省略)
- 4.機器學習
- 5.模型評估(該案例中省略)
3.2 代碼過程
- 導入模塊
from sklearn.neighbors import KNeighborsClassifier- 構造數據集
x = [[0], [1], [2], [3]]
y = [0, 0, 1, 1]- 機器學習 -- 模型訓練
# 實例化API
estimator = KNeighborsClassifier(n_neighbors=2)
# 使用fit方法進行訓練
estimator.fit(x, y)
estimator.predict([[1]])4 小結
-
sklearn的優勢:
- 文檔多,且規範
- 包含的算法多
- 實現起來容易
-
knn中的api
- sklearn.neighbors.KNeighborsClassifier(n_neighbors=5)
問題
1.距離公式,除了歐式距離,還有哪些距離公式可以使用?
2.選取K值的大小?
3.api中其他參數的具體含義?
K-近鄰算法
學習目標
- 掌握K-近鄰算法實現過程
- 知道K-近鄰算法的距離公式
- 知道K-近鄰算法的超參數K值以及取值問題
- 知道kd樹實現搜索的過程
- 應用KNeighborsClassifier實現分類
- 知道K-近鄰算法的優缺點
- 知道交叉驗證實現過程
- 知道超參數搜索過程
- 應用GridSearchCV實現算法參數的調優
1.3 距離度量
學習目標
-
目標
- 知道機器學習中常見的距離計算公式
1 歐式距離(Euclidean Distance):
歐氏距離是最容易直觀理解的距離度量方法, 小學、初中和高中接觸到的兩個點在空間中的距離一般都是指歐氏距離。
舉例:
X=[[1,1],[2,2],[3,3],[4,4]];
經計算得:
d = 1.4142 2.8284 4.2426 1.4142 2.8284 1.41422 曼哈頓距離(Manhattan Distance):
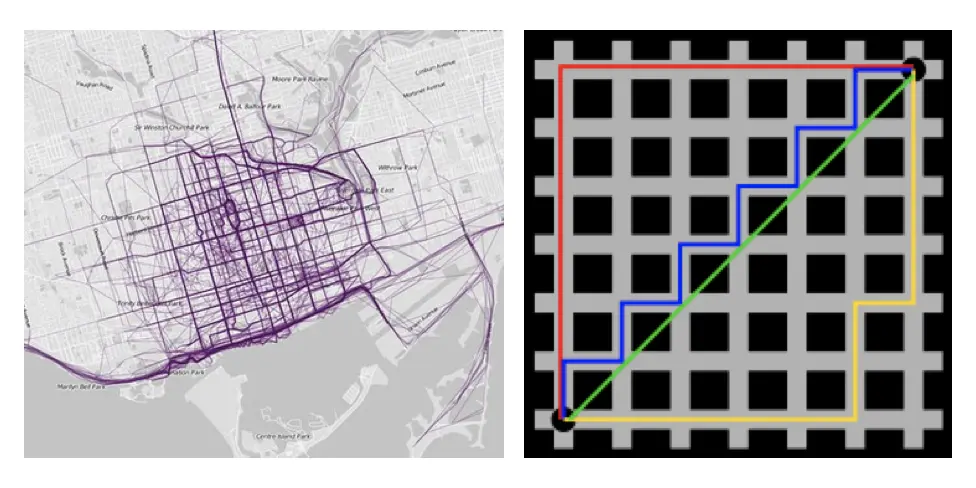
在曼哈頓街區要從一個十字路口開車到另一個十字路口,駕駛距離顯然不是兩點間的直線距離。這個實際駕駛距離就是“曼哈頓距離”。曼哈頓距離也稱為“城市街區距離”(City Block distance)。
舉例:
X=[[1,1],[2,2],[3,3],[4,4]];
經計算得:
d = 2 4 6 2 4 23 切比雪夫距離 (Chebyshev Distance):
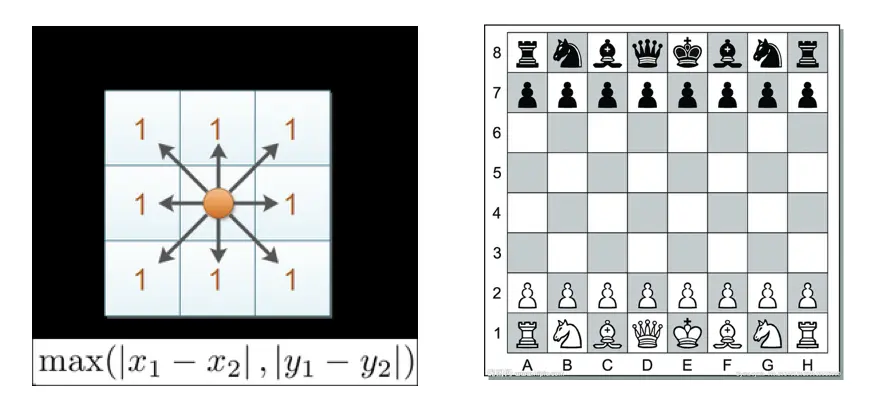
國際象棋中,國王可以直行、橫行、斜行,所以國王走一步可以移動到相鄰8個方格中的任意一個。國王從格子(x1,y1)走到格子(x2,y2)最少需要多少步?這個距離就叫切比雪夫距離。
舉例:
X=[[1,1],[2,2],[3,3],[4,4]];
經計算得:
d = 1 2 3 1 2 14 閔可夫斯基距離(Minkowski Distance):
閔氏距離不是一種距離,而是一組距離的定義,是對多個距離度量公式的概括性的表述。
兩個n維變量a(x11,x12,…,x1n)與b(x21,x22,…,x2n)間的閔可夫斯基距離定義為:
其中p是一個變參數:
當p=1時,就是曼哈頓距離;
當p=2時,就是歐氏距離;
當p→∞時,就是切比雪夫距離。
根據p的不同,閔氏距離可以表示某一類/種的距離。
小結:
1 閔氏距離,包括曼哈頓距離、歐氏距離和切比雪夫距離都存在明顯的缺點:
e.g. 二維樣本(身高[單位:cm],體重[單位:kg]),現有三個樣本:a(180,50),b(190,50),c(180,60)。
a與b的閔氏距離(無論是曼哈頓距離、歐氏距離或切比雪夫距離)等於a與c的閔氏距離。但實際上身高的10cm並不能和體重的10kg劃等號。
2 閔氏距離的缺點:
(1)將各個分量的量綱(scale),也就是“單位”相同的看待了;
(2)未考慮各個分量的分佈(期望,方差等)可能是不同的。
5 標準化歐氏距離 (Standardized EuclideanDistance):
標準化歐氏距離是針對歐氏距離的缺點而作的一種改進。
思路:既然數據各維分量的分佈不一樣,那先將各個分量都“標準化”到均值、方差相等。
$S_k$表示各個維度的標準差
如果將方差的倒數看成一個權重,也可稱之為加權歐氏距離(Weighted Euclidean distance)。
舉例:
X=[[1,1],[2,2],[3,3],[4,4]];(假設兩個分量的標準差分別為0.5和1)
經計算得:
d = 2.2361 4.4721 6.7082 2.2361 4.4721 2.23616 餘弦距離(Cosine Distance)
幾何中,夾角餘弦可用來衡量兩個向量方向的差異;機器學習中,借用這一概念來衡量樣本向量之間的差異。
- 二維空間中向量A(x1,y1)與向量B(x2,y2)的夾角餘弦公式:
- 兩個n維樣本點a(x11,x12,…,x1n)和b(x21,x22,…,x2n)的夾角餘弦為:
即:
夾角餘弦取值範圍為[-1,1]。餘弦越大表示兩個向量的夾角越小,餘弦越小表示兩向量的夾角越大。當兩個向量的方向重合時餘弦取最大值1,當兩個向量的方向完全相反餘弦取最小值-1。
舉例:
X=[[1,1],[1,2],[2,5],[1,-4]]
經計算得:
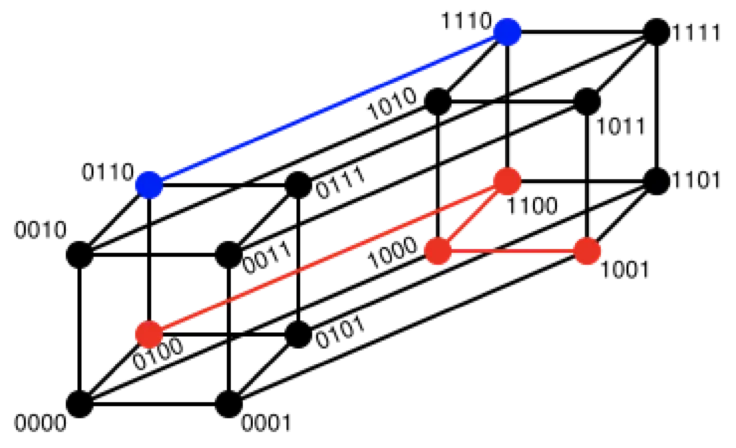
d = 0.9487 0.9191 -0.5145 0.9965 -0.7593 -0.81077 漢明距離(Hamming Distance)【瞭解】:
兩個等長字符串s1與s2的漢明距離為:將其中一個變為另外一個所需要作的最小字符替換次數。
例如:
The Hamming distance between "1011101" and "1001001" is 2.
The Hamming distance between "2143896" and "2233796" is 3.
The Hamming distance between "toned" and "roses" is 3.隨堂練習:
求下列字符串的漢明距離:
1011101與 1001001
2143896與 2233796
irie與 rise漢明重量:是字符串相對於同樣長度的零字符串的漢明距離,也就是説,它是字符串中非零的元素個數:對於二進制字符串來説,就是 1 的個數,所以 11101 的漢明重量是 4。因此,如果向量空間中的元素a和b之間的漢明距離等於它們漢明重量的差a-b。
應用:漢明重量分析在包括信息論、編碼理論、 學等領域都有應用。比如在信息編碼過程中,為了增強容錯性,應使得編碼間的最小漢明距離儘可能大。但是,如果要比較兩個不同長度的字符串,不僅要進行替換,而且要進行插入與刪除的運算,在這種場合下,通常使用更加複雜的編輯距離等算法。
舉例:
X=[[0,1,1],[1,1,2],[1,5,2]]
注:以下計算方式中,把2個向量之間的漢明距離定義為2個向量不同的分量所佔的百分比。
經計算得:
d = 0.6667 1.0000 0.33338 傑卡德距離(Jaccard Distance)【瞭解】:
傑卡德相似係數(Jaccard similarity coefficient):兩個集合A和B的交集元素在A,B的並集中所佔的比例,稱為兩個集合的傑卡德相似係數,用符號J(A,B)表示:
傑卡德距離(Jaccard Distance):與傑卡德相似係數相反,用兩個集合中不同元素佔所有元素的比例來衡量兩個集合的區分度:
舉例:
X=[[1,1,0][1,-1,0],[-1,1,0]]
注:以下計算中,把傑卡德距離定義為不同的維度的個數佔“非全零維度”的比例
經計算得:
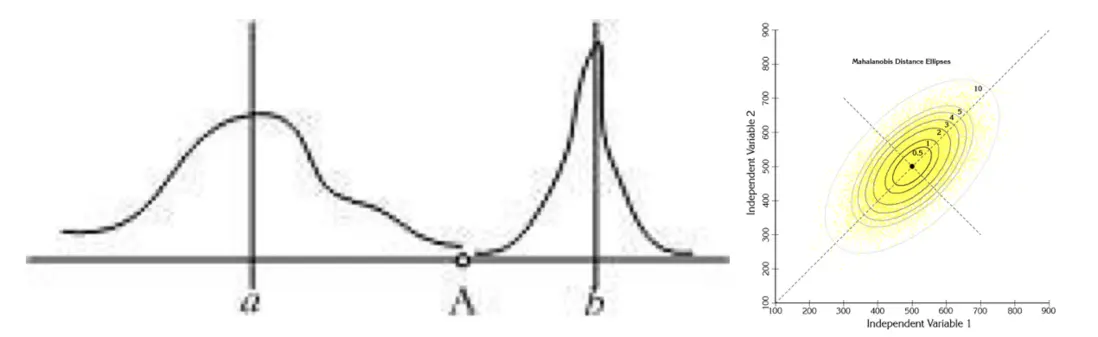
d = 0.5000 0.5000 1.00009 馬氏距離(Mahalanobis Distance)【瞭解】
下圖有兩個正態分佈圖,它們的均值分別為a和b,但方差不一樣,則圖中的A點離哪個總體更近?或者説A有更大的概率屬於誰?顯然,A離左邊的更近,A屬於左邊總體的概率更大,儘管A與a的歐式距離遠一些。這就是馬氏距離的直觀解釋。
馬氏距離是基於樣本分佈的一種距離。
馬氏距離是由印度統計學家馬哈拉諾比斯提出的,表示數據的協方差距離。它是一