一、初識遞歸
遞歸函數 = 終止條件 + 遞歸關係
終止條件: 當大問題被拆解成能輕鬆解決的小問題時,運行終止條件中的邏輯
遞歸關係: 定義如何將大問題拆解為小問題
例子:小名跑步。
例如:小名跑4公里,可以分為(跑1km+再跑3km)-> (跑1km+再跑2km)-> (跑1km+再跑1km)-> (跑完全程)
實現:
public void running(int distance) {
if (distance == 0) { // 終止條件
System.out.println("小名跑完了全程!");
return;
} else {
System.out.println("小名跑了1km");
distance = distance - 1;
System.out.println("還剩" + distance + "km");
running(distance); // 遞歸調用
}
}
@Test
public void test1() {
int distance = 4;
System.out.println("跑步總程:" + distance + "km");
running(distance);
}
輸出:
跑步總程:4km
小名跑了1km
還剩3km
小名跑了1km
還剩2km
小名跑了1km
還剩1km
小名跑了1km
還剩0km
小名跑完了全程!
正如: 二叉搜索樹中的搜索
樹對象:
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {
}
TreeNode(int val) {
this.val = val;
}
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
@Override
public String toString() {
return "TreeNode{" +
"val=" + val +
", left=" + left +
", right=" + right +
'}';
}
}
主要方法:
public TreeNode searchBST(TreeNode root, int val) {
// 終止條件
if (root == null) return null; // 搜索完所有節點,目標節點不存在
if (root.val == val) return root; // 當前節點即為目標節點
// 遞歸(已知:二叉搜索樹(BST)右子樹節點值大於左子樹節點值)
if (val > root.val) return searchBST(root.right, val); // 目標值大於當前節點,開始搜索右子樹
else return searchBST(root.left, val); // 目標值大於當前節點,開始搜索左子樹
}
測試:
@Test
public void test() {
TreeNode treeNode1 = new TreeNode(1);
TreeNode treeNode3 = new TreeNode(3);
TreeNode treeNode7 = new TreeNode(7);
TreeNode treeNode2 = new TreeNode(2,treeNode1,treeNode3);
TreeNode treeNode4 = new TreeNode(4,treeNode2,treeNode7);
TreeNode treeNode = searchBST(treeNode4, 2);
System.out.println(treeNode == null ? null : treeNode.toString());
}
輸出:
TreeNode{val=2, left=TreeNode{val=1, left=null, right=null}, right=TreeNode{val=3, left=null, right=null}}
遞歸三種形式:
1.Memorization緩存:將計算結果保存,避免重複計算
2.Divide and conquer分治:將一個大問題分解成小問題,各個擊破,然後將“小問題的解”組合起來
3.Backracking回溯:逐步嘗試所有滿足條件的結果,一旦發現不可行的解,立即停止。
二、緩存
初始化緩存
如果緩存中存在答案,則直接返回
將計算結果寫入緩存
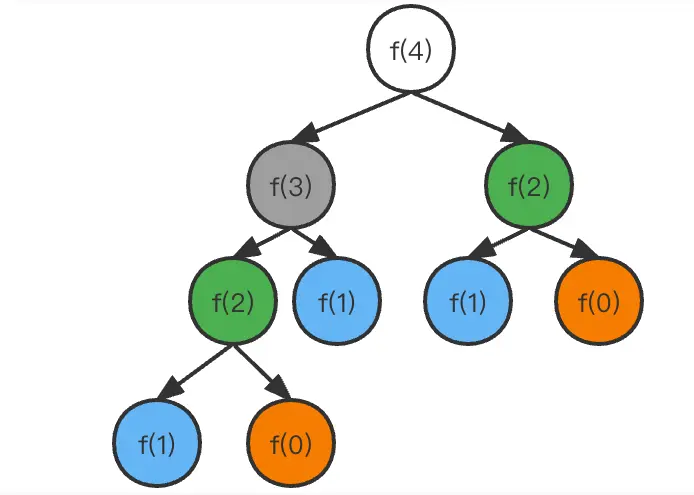
正如: 斐波那契數
題目提示中提到:
f(0) = 0,f(1) = 1
f(n) = f(n - 1) + f(n - 2),其中 n > 1
所以我不難計算出f(2)=1,從上圖我們可以看出f(2)被計算了兩次,所以這裏我們用緩存來減少加法的次數。
public int fib(int n) {
//1.初始化緩存
int[] memo = new int[n+1];
int res = helper(memo, n);
return res;
}
public int helper(int[] memo, int n){
if (n < 2) {
return n;
}
//2.如果緩存中存在答案,則直接返回
if(memo[n]!=0){
return memo[n];
}
//3.將計算結果寫入緩存
memo[n] = helper(memo, n - 1) + helper(memo, n - 2);
return memo[n];
}
測試:
@Test
public void test3(){
int fib = fib(4);
System.out.println(fib);
}
輸出:
3
1
三、分治
把大問題分為一系列小問題
遞歸求解每個子問題
合併每個子問題的結果
二叉搜索樹(BST):左子樹的所有值要比根節點小;右子樹的所有值要比根節點大
正如:LeetCode:98. 驗證二叉搜索樹
public boolean isValidBST(TreeNode root) {
return helper(root, Long.MIN_VALUE, Long.MAX_VALUE);
}
public boolean helper(TreeNode node, long lower, long upper){
if (node == null) {
return true;
}
if (node.val <= lower || node.val >= upper) {
return false;
}
return helper(node.left,lower,node.val) && helper(node.right,node.val,upper);
}
helper方法解讀:
當入參是左子樹節點,要限制所有其他節點比該節點小(限制上界是節點val)
當入參是右子樹節點,要限制所有其他節點比根節點大(限制下界是節點val)
省略樹對象:見上一小節
測試:
@Test
public void test5(){
System.out.println("--------------示例1--------------");
TreeNode treeNode11 = new TreeNode(1);
TreeNode treeNode33 = new TreeNode(3);
TreeNode treeNode22 = new TreeNode(2,treeNode11,treeNode33);
System.out.println(isValidBST(treeNode22));
System.out.println("---------------示例2-------------");
TreeNode treeNode1 = new TreeNode(1);
TreeNode treeNode3 = new TreeNode(3);
TreeNode treeNode6 = new TreeNode(6);
TreeNode treeNode4 = new TreeNode(4, treeNode3, treeNode6);
TreeNode treeNode5 = new TreeNode(5, treeNode1, treeNode4);
System.out.println(isValidBST(treeNode5));
}
示例1:
示例2:
輸出:
--------------示例1--------------
true
---------------示例2-------------
false
1
2
3
4
四、回溯
迭代所有可能的候選對象
試試這個部分候選解決方案
給定候選者,進一步探索
回溯
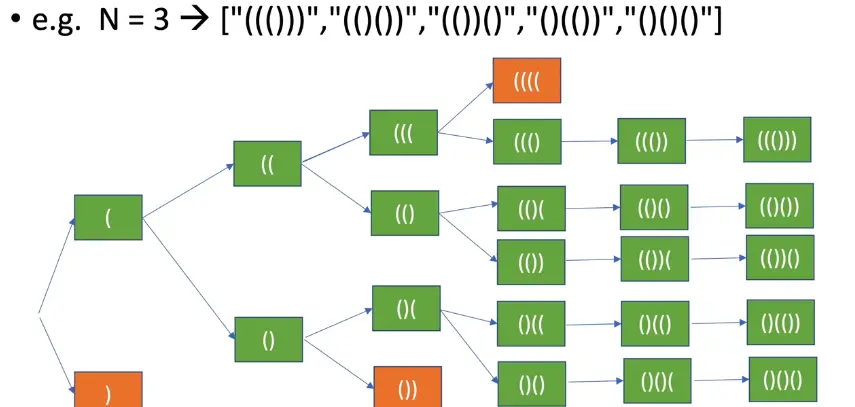
正如: 括號生成
從上文的例子中,可以看出遞歸的題目都可以被畫成樹狀圖。本題要求是“有效的”括號組合,所以肯定不可能由右括號開始。之後就是嘗試列舉所有括號組合情況了,當括號數量達到 2n 這就是我們的終止遞歸的條件了。這裏值得注意的是:左括號的數量不能大於n,而且右括號的數量不能大於左括號的數量,顯然這樣是不符合題目“有效的”括號組合規定的
public void backtrack(List<String> ans, StringBuilder cur, int open, int close, int max) {
// 終止條件
if (cur.length() == 2 * max) {
ans.add(cur.toString());
return;
}
// 左括號不能超過最大值
if (open < max) {
// 試探添加左括號
backtrackV2(ans, cur.append("("), open + 1, close, max);
// 回溯
cur.deleteCharAt(cur.length() - 1);
}
// 右括號數量不能大於左括號數量
if (close < open) {
// 試探添加右括號
backtrackV2(ans, cur.append(")"), open, close + 1, max);
// 回溯
cur.deleteCharAt(cur.length() - 1);
}
}
public List<String> generateParenthesis(int n) {
List<String> ans = new ArrayList<String>();
backtrack(ans, new StringBuilder(), 0, 0, n);
return ans;
}
測試
@Test
public void test6(){
List<String> strings = generateParenthesis(3);
System.out.println(strings);
}
輸出:
[((())), (()()), (())(), ()(()), ()()()]