寫在前面
關於Games101深度解析參考了很多佬的文章,並且加上了自己的理解。主要感覺games101課程裏面還有很多由於時間原因都沒講的很詳細,略過了很多,所以我對於課程中困難的知識點進行了更多的步驟思路解釋,希望能對正在學習這篇課程的後者提供更清晰的思路。
本文建議配上games101視頻以及games101網站中的PDF配合學習https://sites.cs.ucsb.edu/~lingqi/teaching/games101.html
這一章含有大量線代的幾何知識,對於線代的幾何理解可以跳到這學習(一步一步看完基本上就沒有太大的問題了):https://www.bilibili.com/video/BV1Ys411k7yQ/?spm_id_from=333.337.search-card.all.click&vd_source=93699bcffa78a7a266992d3b23c6dc20
這一章由於知識點都較為簡單,所以看起來會很雜,但是後面從第二章開始就開始有章法了。剛開始的數學基礎知識就不再提了,我們從線代在圖形學的應用開始。
參考文章:
https://zhuanlan.zhihu.com/p/394932478
https://iewug.github.io/book/GAMES101.html#2-3d-transformation
https://sites.cs.ucsb.edu/~lingqi/teaching/games101.html
https://caterpillarstudygroup.github.io/GAMES101_mdbook/index.html
向量叉乘的應用
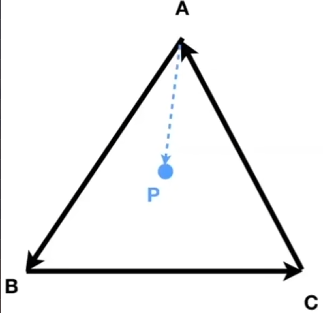
上圖中,判斷p是否在三角形ABC的內側,只用將p點與ABC三點相連接,然後再分別叉乘三個邊,看結果的符號是否一致,若一致,那麼就在內側,反之亦然。
比如AP叉乘AB,然後BP叉乘BC,然後CP叉乘CA,他們的符號都是一致的,則P就在三角形的裏面
指令矩陣在圖形學的應用
上面的矩陣做的就是:在二維裏面,我們把整個圖形以y軸為對稱軸做一個對稱圖形。
那麼我們y軸就不用變,把x的數都換個符號就行。上面不止是指令矩陣的角度,線性變換也是這個角度。
幾種變換
根據上面的內容我們就可以得到下面的效果
-
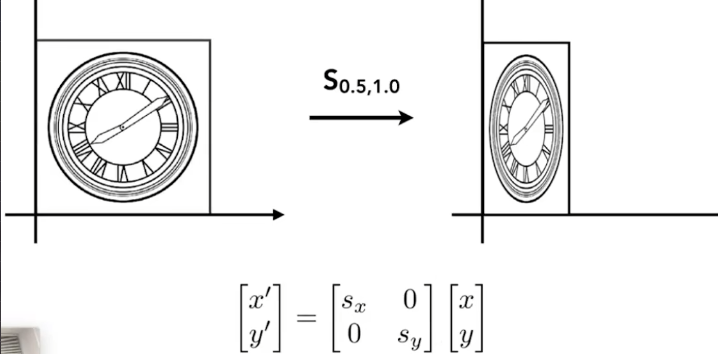
縮放矩陣
-
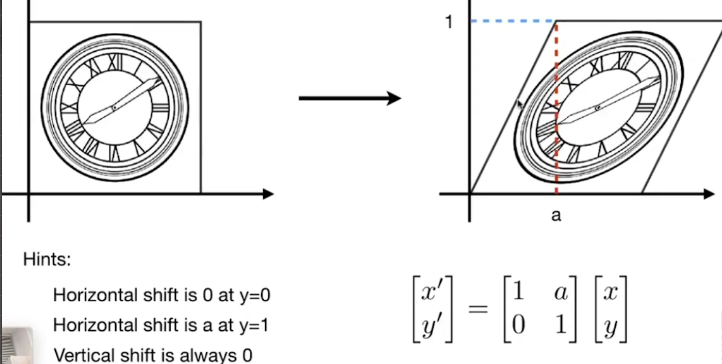
拉伸變換
-
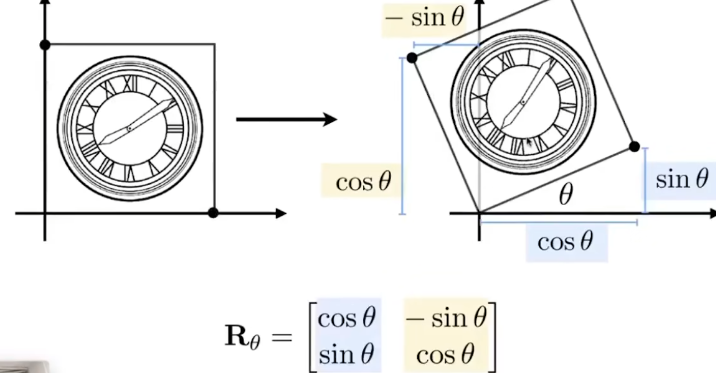
旋轉變換
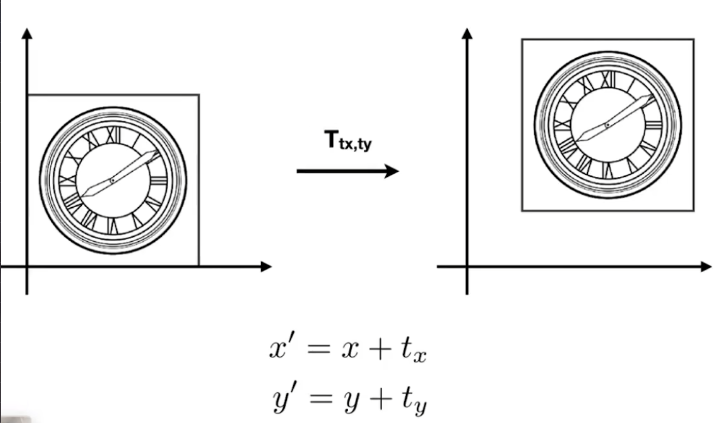
平移變換
我們前面看了這麼多變換都是基於原點的變換,但是如果是下面的這個變換(平移)我們該怎麼表示呢?
我們這個時候就發現了,我們常規的矩陣往往都只能表示一個向量,但是我們明白,向量平移是不會改變什麼的,常規矩陣就是沒有辦法去表示平移這個動作。
這個時候我們就引入一個新的東西:齊次座標(homogeneous coordinates)
齊次座標是用N+1個數來表示N維座標的一種方式。
要製作二維齊次座標,我們只需在現有座標中增加一個額外的變量w,這個w並不代表更高維度的一個座標,簡單説就是表示這裏的(x,y)是一個向量或者是一個點。
因此,笛卡爾座標中的一點,(X,Y)在齊次座標中就變成了(x,y,w)。在w=1的時候,齊次座標就是一個點,而w=0的時候,齊次座標表示的就是一個向量。而笛卡兒座標中的X和Y在齊次座標中的x、y和w則重新表達為(這裏把所有的座標都除了一個\(w\) ,這樣\(w\) 的值就必定是1,那就是一個向量)
那怎麼應用到實際的平移中呢,就是以下的變換。這樣的變換成功表示了每一個平移的點,而且直觀的有了一個平移的指令矩陣
歐氏空間中數學證明:兩條平行線可以相交
考慮以下歐氏空間的線性系統。
而我們知道,由於 \(C \neq D\),所以上述方程沒有解。如果 \(C = D\),那麼兩條線是相同的(重疊的)。
讓我們重寫投影空間的方程,將 \( x \) 和 \( y \) 分別替換為 \( x/w \),\( y/w \)。
現在,我們有一個解,(x, y, 0),因為 (C-D)w = 0,所以 w = 0。因此,兩條平行線在 (x, y, 0) 處相交。
(x, y, 0) 在幾何上代表一條沒有起點與終點,也沒有長度的射線,它只有方向。
點與向量的加減
- vector + vector = vector
- point - point = vector
- point + vector = vector
- point + point = 兩點的中點 (因為\((x_1,y_1,1)\) + \((x_2,y_2,1)\) = \((x_1+x_2,y_1+y_2,2)\) = \((\frac{x_1+x_2}{2},\frac{y_1+y_2}{2},1)\)))
仿射變換
像這樣線性變換之後加上平移量的變換叫做放射變換
所有的放射變換都可以寫成齊次座標的形式
[!danger]
注意: 在上面的變換中我們能夠發現,是先線性變換再進行平移的
- 縮放矩陣
- 旋轉矩陣
- 平移矩陣 :
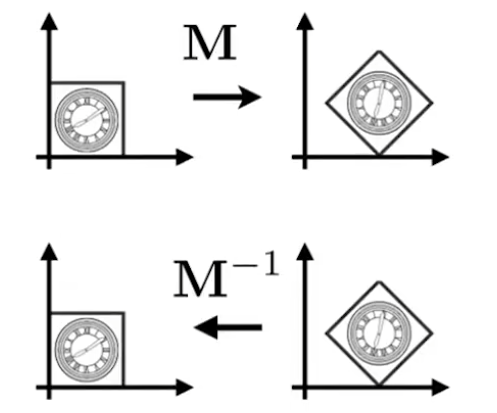
逆變換
[!note]
逆變換剛好對應矩陣中:一個矩陣 x 該矩陣的逆矩陣 = 單位矩陣(什麼都沒做)
值得注意的是,如果旋轉負角度,我們就能發現:
[!note]
旋轉矩陣的逆矩陣就是旋轉矩陣的轉置矩陣:\({R_\alpha}^T={R_\alpha}^{-1}\)
[!note] 如果一個矩陣的逆等於他的轉置,那麼我們稱此矩陣為正交矩陣
\(\mathbf{R}(\alpha) = \begin{pmatrix}\cos \alpha & -\sin \alpha \\\sin \alpha & \cos \alpha \\\end{pmatrix}\) \(\mathbf{R}(-\alpha) = \begin{pmatrix}\cos \alpha & \sin \alpha \\-\sin \alpha & \cos \alpha \\\end{pmatrix} ={R_\alpha}^T={R_\alpha}^{-1}\)
矩陣的乘法沒有交換律:變換的順序會導致結果不同
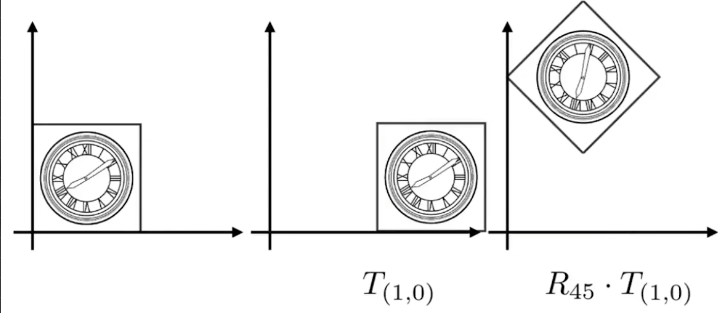
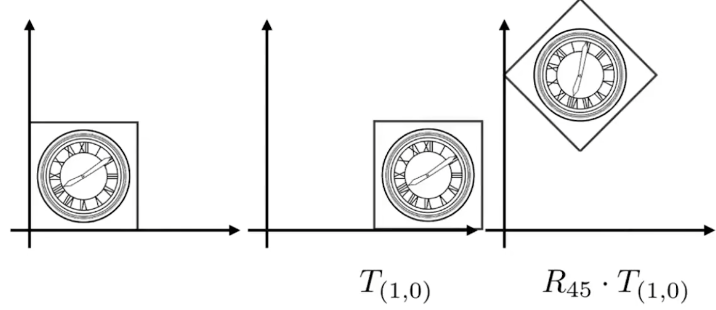
先平移再旋轉如下:
先旋轉再平移如下:
這裏就能夠體現出兩者的變換順序不同對應着矩陣的乘法沒有交換律。
當然,多個線性變換由於有結合律的緣故,我們可以對線性變換先進行線性變換,最後得到一個大的線性變換再對其最開始的向量進行線性變換都行
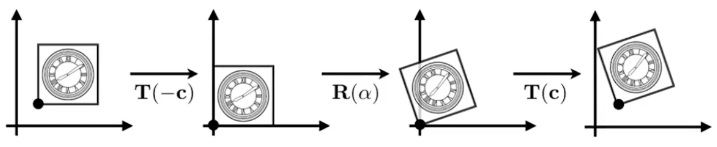
任意點的旋轉
我們前面只知道怎麼沿着原點旋轉,如果要沿着其他的一個點旋轉一個圖形,我們就可以先平移到原點,然後進行旋轉,最後我們旋轉完之後再平移回去是一樣的。