此分類用於記錄吳恩達深度學習課程的學習筆記。
課程相關信息鏈接如下:
- 原課程視頻鏈接:[雙語字幕]吳恩達深度學習deeplearning.ai
- github課程資料,含課件與筆記:吳恩達深度學習教學資料
- 課程配套練習(中英)與答案:吳恩達深度學習課後習題與答案
本篇為第二課第一週的課程習題和代碼實踐部分筆記。
1. 理論習題
【中英】【吳恩達課後測驗】Course 2 - 改善深層神經網絡 - 第一週測驗
還是擺一下這位博主的鏈接,本週理論習題沒什麼難度,基本就是對理論內容的重複,因此就不再展開了。
我們把重點放在下面的代碼實踐部分。
2.代碼實踐
依舊先上鍊接:
吳恩達深度學習初始化與正則化
在這篇博客裏,博主手動構建了幾種初始化,正則化以及梯度檢驗的方法。
我依舊在這裏給出更偏向現有框架的版本,應用本週瞭解到的新技術到我們從一開始就在使用的貓狗二分類數據集上。
還是需要提前説明的是:在使用完善框架內置計算的前提下,進行梯度檢驗的意義不大,梯度檢驗本身也只是一個檢驗梯度計算是否出錯的技術,在計算不出錯的情況下不能直接幫助擬合,目前也幾乎不再使用,就不在筆記裏出現了。
我們重點展開一下權重初始化和正則化兩部分。
2.1 權重初始化
我們在第一課第三週裏介紹了初始化的概念,又在本週的最後一部分內容裏介紹了科學的權重初始化的思想,現在看看它們的效果。
在第一課裏,我們通過一層層豐富網絡結構,讓分類準確率從50%提升到了接近70%。實際上,在一開始,PyTorch框架就已經根據我們設置的層進行了相應的權重初始化。
我們之前設置Linear線性層,因此框架就自動進行了 He權重初始化。
先看一下我們上次更新的網絡結構:
class NeuralNetwork(nn.Module):
def __init__(self):
super().__init__()
self.flatten = nn.Flatten()
# 隱藏層
self.hidden1 = nn.Linear(128 * 128 * 3, 5)
self.hidden2 = nn.Linear(5, 5)
self.hidden3 = nn.Linear(5, 3)
self.ReLU = nn.ReLU()
# 輸出層
self.output = nn.Linear(3, 1)
self.sigmoid = nn.Sigmoid()
def forward(self, x):
x = self.flatten(x)
x = self.hidden1(x)
x = self.ReLU(x)
x = self.hidden2(x)
x = self.ReLU(x)
x = self.hidden3(x)
x = self.ReLU(x)
x = self.output(x)
x = self.sigmoid(x)
return x
實際上,權重初始化的邏輯被封裝在了這幾句裏:
# PyTorch邏輯:對線性層自動進行 He 權重初始化
# He 權重初始化 也叫 Kaiming 初始化 只是一個是提出者的姓,一個是名,僅此而言。
self.hidden1 = nn.Linear(128 * 128 * 3, 5)
self.hidden2 = nn.Linear(5, 5)
self.hidden3 = nn.Linear(5, 3)
self.output = nn.Linear(3, 1)
也就是説,在PyTorch框架的構造方法裏,我們每設置一個線性層,框架就會自動對其進行 He 初始化。
瞭解基礎邏輯後,我們看幾個需要展開的問題。
(1)為什麼PyTorch框架的初始化針對層而不是激活函數?
回憶一下我們在上一篇里加粗的一句話:不同激活函數會改變信號統計特性,所以需要不同的初始化。
也就是説,選擇初始化方式的依據不應該是該層的激活函數嗎?
再看一下我們總結的兩類初始化:
| 初始化方法 | 核心思想 | 適用激活函數 | 公式 | 舉例説明 |
|---|---|---|---|---|
| Xavier (Glorot) | 讓輸入輸出方差一致 | Sigmoid / Tanh | \(Var(W)=\frac{1}{n_{in}+n_{out}}\) | 若一層輸入神經元 100 個、輸出 50 個:
\(Var(W)=1/(150)=0.0067\) |
| He (Kaiming) | 針對 ReLU 激活的特性調整 | ReLU / Leaky ReLU | \(Var(W)=\frac{2}{n_{in}}\) | 輸入 100 個神經元 → \(Var(W)=0.02\) |
結合我們的網絡結構,會發現一個問題:我們的輸出層實際上使用的也是He 初始化,可該層的激活函數是Sigmoid,不應該用Xavier 初始化才更合理嗎?
那麼,PyTorch作為目前最流行的成熟框架之一,為什麼會出現這種紕漏?
其實這並不是框架的紕漏,而是設計方式不同導致的結果,我們先説原理。
(2)層和激活函數在初始化中的關係?
先説結論:初始化的推導主要基於“線性變換的輸入輸出方差”,而不是激活函數本身。
也就是説,初始化天然與線性層更緊密相關,而非與激活函數綁定。
要理解這句話,我們先把初始化的核心目標講清楚:
初始化的目的,是讓信號在層與層之間不要越來越大,也不要越來越小。
而信號在層間傳播,第一步永遠是通過線性層,也就是一次矩陣乘法,這一步決定了信號的基礎規模——也就是“方差是否在傳播時保持穩定”。
大部分初始化方法都是從這一層面推導出來的:設定權重的範圍,讓線性層的輸出不要突然變得特別大或特別小。
因此,初始化的數學起點是線性層的輸入和輸出的大小,而不是激活函數本身。這是為什麼 PyTorch 會把初始化綁定在線性層上:從框架角度看,這一步才是真正需要“方差控制”的核心點。
那與我們之前説的 “不同激活函數會改變信號統計特性,所以需要不同的初始化” 是不是矛盾?
其實並不矛盾,它們是兩個層次的邏輯:
還是先説結論:因為激活函數對信號的“壓縮方式”不同,所有理論上需要不同的初始化做“補償”。
初始化需要讓線性層輸出穩定,是為了給下一步的激活創造良好條件,這一層面初始化和線性層的“輸入/輸出規模”更相關,框架默認以這一邏輯為主。
而在線性組合的基礎上,不同激活函數會進一步改變信號:
- ReLU 會把一半輸入砍成 0,使方差變小
- Sigmoid 會把大輸入“壓平”,讓梯度變小
- Tanh 會把兩端推向 -1 或 1,也會讓梯度變小
也就是説:激活函數會改變方差信號的處理方式,所以理論上需要不同的初始化去匹配它。
例如: - ReLU 會讓方差減少,所以 He 初始化會把權重再放大一點
- Sigmoid 會壓扁兩端,所以 Xavier 初始化讓權重相對小一些
但這一步是在線性變換之後發生的,是“第二層邏輯”。
總結一下:所有初始化都是先為了線性部分服務,再衍生出適配激活函數的特化版本。
打個比方:
做一道菜時,首先要把基本味道調對,基本味道就相當於線性層的方差穩定,它是菜好不好吃的核心。
然後才根據不同的食材——如辣的、甜的、酸的, 再做額外調味,讓整道菜平衡好吃,這些額外調味就相當於針對激活函數的特化,讓菜更好吃。
(3)PyTorch的設計邏輯?
首先這句 “不同激活函數會改變信號統計特性,所以需要不同的初始化” 是正確的。
理論上確實應該:
- ReLU 類激活配 He 初始化
- Sigmoid / Tanh 配 Xavier 初始化
但 PyTorch 的默認行為並不會根據激活函數自動切換初始化,其原因主要有三點:
- 框架在創建 Linear 層時,並不知道你之後會接什麼激活函數。
激活函數是在 forward 裏使用的,可能隨時更換,也可能不用,因此無法在層創建時提前決定正確的初始化方式。 - 初始化的推導主要基於“線性變換的輸入輸出方差”,而不是激活函數本身。
初始化天然與線性層更緊密相關,而非與激活函數綁定。 - PyTorch 選擇了一個在大多數情況下都安全、穩妥的默認方案。
默認提供偏向 ReLU 的 Kaiming(He)初始化,使大部分網絡都能正常訓練。如果用户需要嚴格匹配某個激活函數,再手動覆蓋即可。
總的來説,我們的輸出層雖然接了 Sigmoid,PyTorch 仍然使用了 He 初始化——框架並不是做錯了,而是在不知道具體情況下給出了一個“通用但不一定最優”的默認值。
(4)人工完善特化邏輯
瞭解完原因,我們就可以完善邏輯了,我們修改輸出層的權重初始化方法為Xavier 初始化,代碼如下:
class NeuralNetwork(nn.Module):
def __init__(self):
super().__init__()
self.flatten = nn.Flatten()
self.hidden1 = nn.Linear(128 * 128 * 3, 5)
self.hidden2 = nn.Linear(5, 5)
self.hidden3 = nn.Linear(5, 3)
self.ReLU = nn.ReLU()
self.output = nn.Linear(3, 1)
self.sigmoid = nn.Sigmoid()
# 對輸出層進行Xavier初始化
init.xavier_uniform_(self.output.weight)
def forward(self, x):
x = self.flatten(x)
x = self.hidden1(x)
x = self.ReLU(x)
x = self.hidden2(x)
x = self.ReLU(x)
x = self.hidden3(x)
x = self.ReLU(x)
x = self.output(x)
x = self.sigmoid(x)
return x
(5)和隨機初始化對比效果
現在我們已經有了權重初始化合理的網絡,現在再給出一版完全使用隨機初始化的版本,我們實際運行一下,看看二者的差距。
隨機初始化的模型代碼如下:
class NeuralNetwork(nn.Module):
def __init__(self):
super().__init__()
self.flatten = nn.Flatten()
self.hidden1 = nn.Linear(128 * 128 * 3, 5)
self.hidden2 = nn.Linear(5, 5)
self.hidden3 = nn.Linear(5, 3)
self.output = nn.Linear(3, 1)
self.ReLU = nn.ReLU()
self.sigmoid = nn.Sigmoid()
# 對每一層權重進行隨機初始化
for layer in [self.hidden1, self.hidden2, self.hidden3, self.output]:
init.uniform_(layer.weight, a=-0.1, b=0.1) # (-1,1)間隨機初始化
def forward(self, x):
x = self.flatten(x)
x = self.hidden1(x)
x = self.ReLU(x)
x = self.hidden2(x)
x = self.ReLU(x)
x = self.hidden3(x)
x = self.ReLU(x)
x = self.output(x)
x = self.sigmoid(x)
return x
對比部分的完整代碼依舊放在文末,我們來看看一下結果:
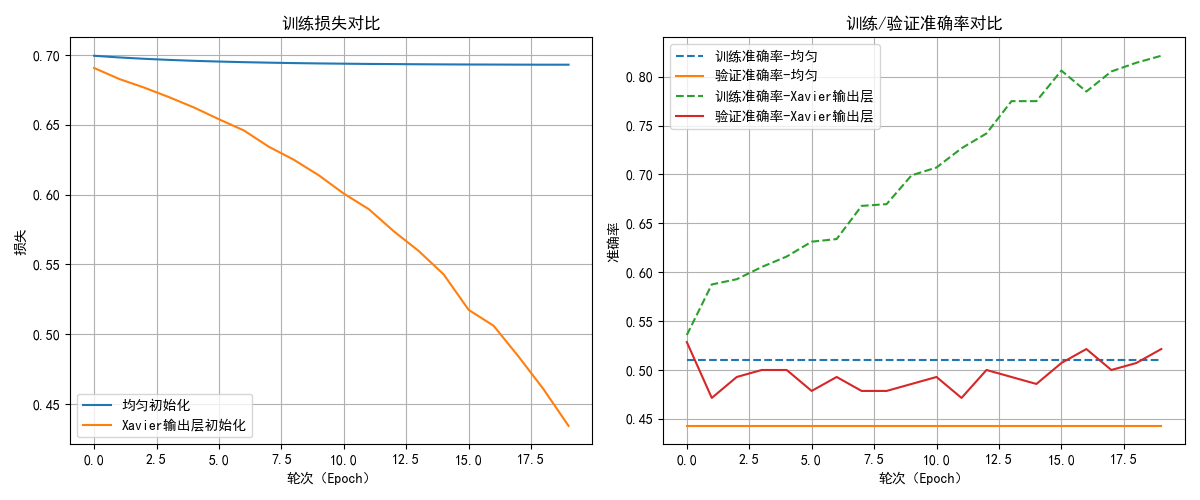
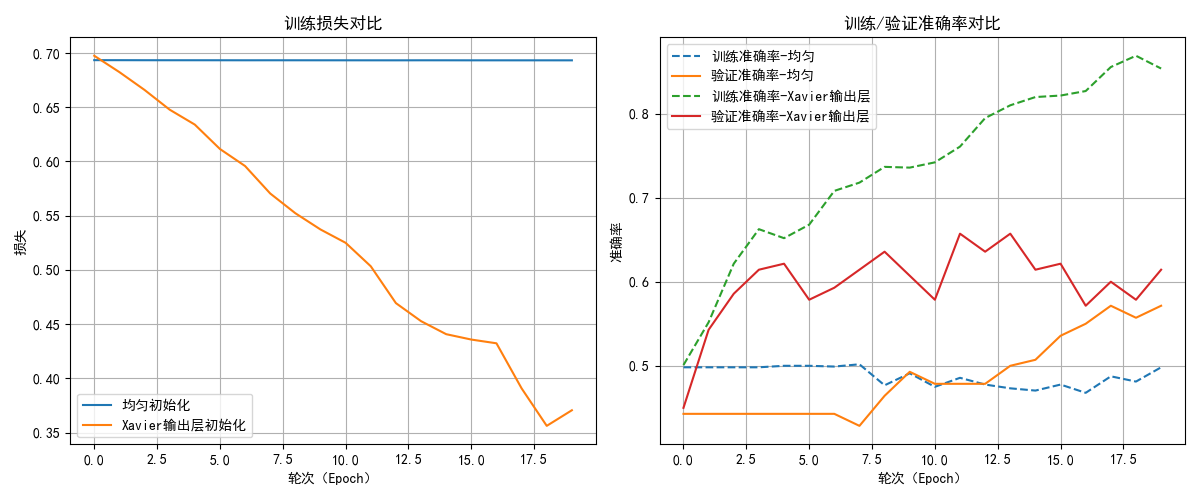
以20輪測試,我選取了其中兩次的測試結果,我們來分析一下結果:
- 對於損失,隨機初始化幾乎次次都出現了梯度消失的現象,導致損失下降緩慢。
而合適的初始化則在穩定地進行收斂。 - 第一次的隨機初始化中的梯度消失導致模型幾乎無法學到任何規律,只是在胡亂猜測,導致了訓練和測試的準確率不佳,有時甚至降到了50%以下,這代表模型沒有任何實用價值,即使有所起伏,其上限也不高,這就相當於“一開始走錯了路,在一條彎路上走到底。”
- 合適的初始化則在準確率的表現上更好一些,如果加大輪次,甚至出現了過擬合現象,這代表其確實在學習圖像的規律。
總結一下,隨機初始化導致梯度消失和訓練不穩定,使模型難以學習有效特徵,而合適的初始化能夠保證梯度穩定,加速收斂,是深度神經網絡訓練中不可或缺的一步。
2.2 正則化
(1)構建一個可能出現過擬合的深層神經網絡
在本週理論第二部分的筆記裏,我們知道正則化的出現是為了緩解複雜網絡對的數據過擬合問題。
因此,為了更合理的使用正則化,我們首先應構建一個可能出現過擬合的深層神經網絡。
提前強調一個地方,在理論學習中,課程為了幫助我們更好地理解,基本使用的都是三個或者五個這樣較少的特徵數。
而我們一開始選擇的數據集是圖片。
對於一幅彩色圖像而言,每個像素由三個通道值(R、G、B)共同表示。
因此,一幅彩色圖像的特徵數為:像素點個數 * 通道數。
我們繼續使用進行合適初始化後的網絡結構,
其實,其中有一個很不合理的層級設計,就在這裏:
self.hidden1 = nn.Linear(128 * 128 * 3, 5)
我們把一個接近 50,000 維的輸入,一下子壓縮成 5 維。
這在深度學習裏非常不合理,相當於:
輸入圖片(49152 個數字)=一本 4.9 萬字的長篇小説
第一層輸出只有 5 維 = 只允許你寫 5 個字來總結它
(感覺GPT是在用畫畫的方式寫中文)
其實,在實際使用中我們很少用全連接網絡去學習圖片,我們後面再提。
總之,這種壓縮過於激進,相當於極端的信息損毀,這會讓模型基本無法學到有效的圖像特徵。
那為什麼還能有65%的準確率?
因為即使把圖像極端壓縮成 5 維,網絡仍能從這 5 個自動學習的統計特徵中抓住背景偏差、形狀差異、亮度模式等低級線索,從而得到 60%~70% 的準確率。
並不是因為這個結構合理,而是:任務容易、數據有偏差、壓縮層仍可學習、類別天然可分、神經網絡具有強大的非線性能力。
總結一下:現在的準確率主要靠網絡本身的“泛化能力 + 非線性能力”撐起來,而網絡結構在拖後腿。
(2)修改網絡結構實現對訓練集的過擬合
按照剛剛的邏輯,現在,我們更新網絡結構如下:
class NeuralNetwork(nn.Module):
def __init__(self):
super().__init__()
self.flatten = nn.Flatten()
self.hidden1 = nn.Linear(128 * 128 * 3, 1024)
self.hidden2 = nn.Linear(1024, 512)
self.hidden3 = nn.Linear(512, 128)
self.hidden4 = nn.Linear(128, 32)
self.hidden5 = nn.Linear(32, 8)
self.hidden6 = nn.Linear(8, 3)
self.relu = nn.ReLU()
# 輸出層
self.output = nn.Linear(3, 1)
self.sigmoid = nn.Sigmoid()
init.xavier_uniform_(self.output.weight)
def forward(self, x):
x = self.flatten(x)
x = self.relu(self.hidden1(x))
x = self.relu(self.hidden2(x))
x = self.relu(self.hidden3(x))
x = self.relu(self.hidden4(x))
x = self.relu(self.hidden5(x))
x = self.relu(self.hidden6(x))
x = self.sigmoid(self.output(x))
return x
你也可以試試構建更深層次,神經元下降更平緩的網絡,但我並不建議在本次實踐中這麼做。
一來,你的硬件可能帶不動更復雜的網絡結構,會報內存不足,無法訓練(資源足夠可以忽略)。
二來,針對貓狗二分類任務,我們不會繼續在全連接的網絡複雜度上下功夫了,在圖像的學習上,我們後面學習的卷積網絡的性能對現在的全連接網絡簡直就是降維打擊。
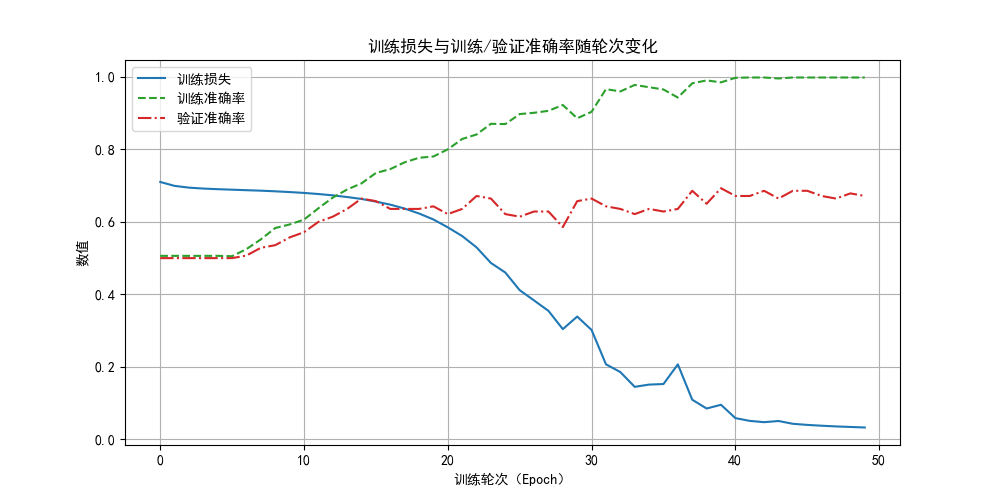
現在我們看看訓練結果:
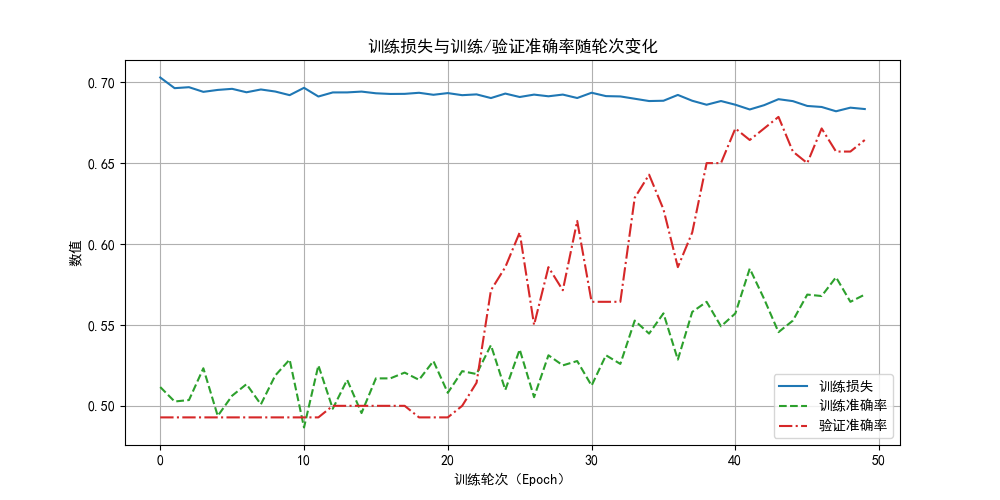
經過50輪的訓練(之後會學到的學習率優化算法會更快達到這一結果,現在還是用笨方法)後,我們可以看到,模型的損失極小,且在訓練集上的準確率已經近乎100% 了,可驗證集的準確率還是在65%~70%波動,這時候,我們就可以説,模型已經過擬合了。
現在我們已經有了前提條件了,來試試正則化的效果吧。
(3)應用L2正則化
在Pytorch框架裏,L2正則化被封裝在了優化器模塊裏。
我們看看之前這部分的代碼:
optimizer = optim.SGD(model.parameters(), lr=0.01)
# 使用隨機梯度下降法(Stochastic Gradient Descent,SGD)反向傳播,學習率為0.01
# 你也可以自己調試一下其他學習率,看看效果。
現在,要使用L2正則化,只需要增加一個參數:
optimizer = optim.SGD(model.parameters(), lr=0.01,weight_decay=0.001)
# weight_decay=0.001 正則化參數設置為0.001
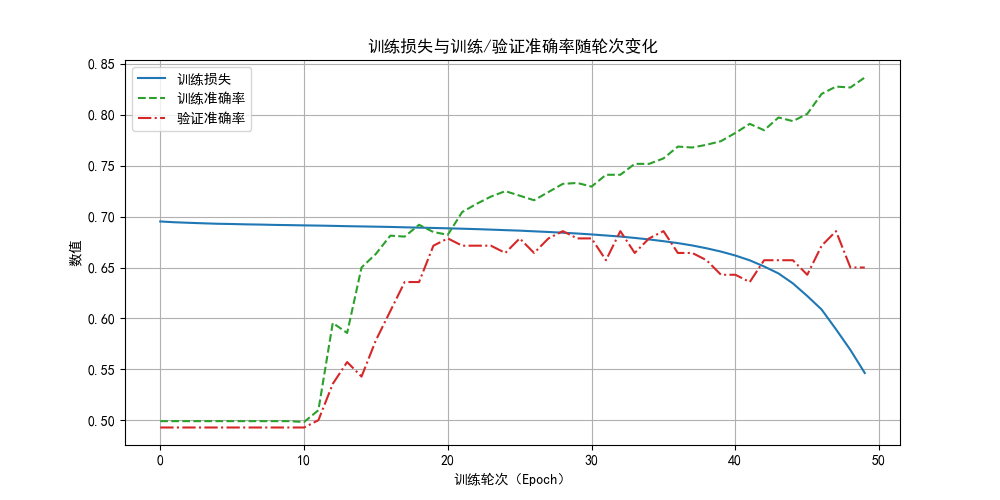
不改變其他任何內容,來看看結果:
可以看到,相比之前近乎100%的準確率,現在的訓練準確了只達到了85%左右,雖然測試的準確率變化不大,但確實緩解了過擬合情況。
那如果增大正則化參數,會不會更好一點? 我們試試:
optimizer = optim.SGD(model.parameters(), lr=0.01,weight_decay=0.01)
看看結果,確實沒有過擬合情況了,因為現在欠擬合了。
強調一下,從本質上講,L2 正則化是在“限制模型的學習能力”。
因此,正則化參數作為又一個超參數,也需要我們一點點調試,讓其更適合我們的任務。
(4)應用dropout正則化
在Pytorch框架裏,dropout正則化不同L2正則化,它被封裝在了網絡結構模塊裏。
來看看增加了dropout模塊後的模型結構:
class NeuralNetwork(nn.Module):
def __init__(self):
super().__init__()
self.flatten = nn.Flatten()
self.hidden1 = nn.Linear(128 * 128 * 3, 1024)
self.hidden2 = nn.Linear(1024, 512)
self.hidden3 = nn.Linear(512, 128)
self.hidden4 = nn.Linear(128, 32)
self.hidden5 = nn.Linear(32, 8)
self.hidden6 = nn.Linear(8, 3)
self.relu = nn.ReLU()
# Dropout 層
self.dropout = nn.Dropout(p=0.5) # p:丟棄概率
self.output = nn.Linear(3, 1)
self.sigmoid = nn.Sigmoid()
init.xavier_uniform_(self.output.weight)
def forward(self, x):
x = self.flatten(x)
x = self.relu(self.hidden1(x))
x = self.dropout(x) # Dropout
x = self.relu(self.hidden2(x))
x = self.dropout(x) # Dropout
x = self.relu(self.hidden3(x))
x = self.dropout(x) # Dropout
x = self.relu(self.hidden4(x))
x = self.dropout(x) # Dropout
x = self.relu(self.hidden5(x))
x = self.dropout(x) # Dropout
x = self.relu(self.hidden6(x))
x = self.dropout(x) # Dropout
x = self.sigmoid(self.output(x))
return x
optimizer = optim.SGD(model.parameters(), lr=0.01)
這樣,我們就可以通過調整 P 來進行dropout正則化,來看看效果如何:
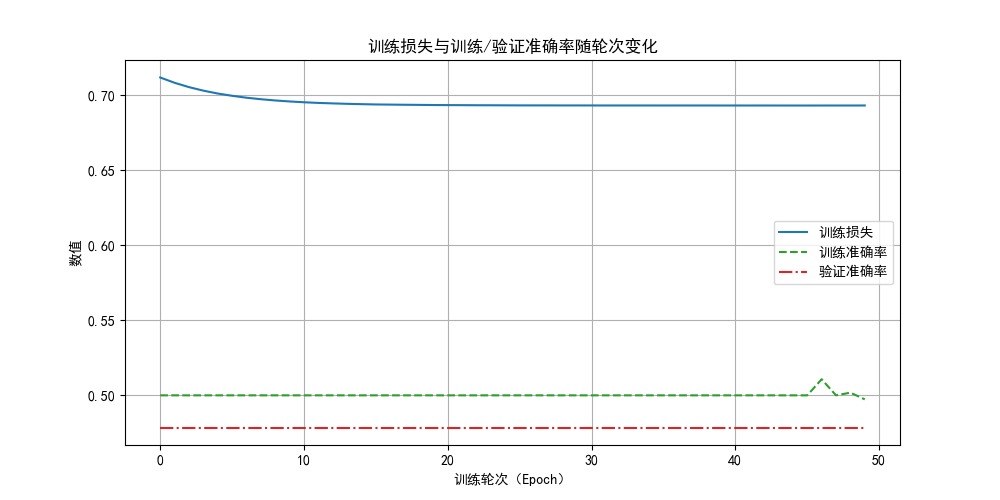
相比L2,dropout正則化有一些比較明顯的區別,但也同樣緩解了過擬合問題:
- 損失下降緩慢:這是因為每次迭代丟失了神經元,增加了隨機性,讓反向傳播的效果沒有那麼明顯。
- 驗證準確率高於訓練準確率:這是因為在驗證時我們使用的是完整網絡,而訓練時只用其中一部分。
值得一提的是,由於dropout正則化隨機丟棄神經元的特性,往往需要更多的訓練輪次,大家可以自行嘗試看看效果,本篇內容就到此為止了。
在應用了新技術後,我們發現,雖然緩解了過擬合現象,可好像還是沒有提高驗證準確率,到底如何才能訓練一個可實用的貓狗分類器呢?我們繼續學習就會得到答案。
3.附錄
3.1權重初始化部分完整代碼:
import torch
import torch.nn as nn
import torch.optim as optim
from torch.nn import init
from torchvision import datasets, transforms
from torch.utils.data import DataLoader, random_split
import matplotlib.pyplot as plt
transform = transforms.Compose([
transforms.Resize((128, 128)),
transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,))
])
dataset = datasets.ImageFolder(root='./cat_dog', transform=transform)
train_size = int(0.8 * len(dataset))
val_size = int(0.1 * len(dataset))
test_size = len(dataset) - train_size - val_size
train_dataset, val_dataset, test_dataset = random_split(dataset, [train_size, val_size, test_size])
train_loader = DataLoader(train_dataset, batch_size=32, shuffle=True)
val_loader = DataLoader(val_dataset, batch_size=32, shuffle=False)
test_loader = DataLoader(test_dataset, batch_size=32, shuffle=False)
class NeuralNetwork(nn.Module):
def __init__(self, init_type='uniform'):
super().__init__()
self.flatten = nn.Flatten()
self.hidden1 = nn.Linear(128*128*3, 5)
self.hidden2 = nn.Linear(5, 5)
self.hidden3 = nn.Linear(5, 3)
self.ReLU = nn.ReLU()
self.output = nn.Linear(3, 1)
self.sigmoid = nn.Sigmoid()
# 初始化
if init_type == 'uniform':
for layer in [self.hidden1, self.hidden2, self.hidden3, self.output]:
init.uniform_(layer.weight, a=-0.1, b=0.1)
elif init_type == 'xavier_output':
init.xavier_uniform_(self.output.weight)
def forward(self, x):
x = self.flatten(x)
x = self.ReLU(self.hidden1(x))
x = self.ReLU(self.hidden2(x))
x = self.ReLU(self.hidden3(x))
x = self.sigmoid(self.output(x))
return x
def train_model(model, epochs=20):
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
model.to(device)
criterion = nn.BCELoss()
optimizer = optim.SGD(model.parameters(), lr=0.01)
train_losses = []
train_accuracies = []
val_accuracies = []
for epoch in range(epochs):
model.train()
epoch_train_loss = 0
correct_train = 0
total_train = 0
for images, labels in train_loader:
images, labels = images.to(device), labels.to(device).float().unsqueeze(1)
outputs = model(images)
loss = criterion(outputs, labels)
optimizer.zero_grad()
loss.backward()
optimizer.step()
epoch_train_loss += loss.item()
preds = (outputs > 0.5).int()
correct_train += (preds == labels.int()).sum().item()
total_train += labels.size(0)
avg_train_loss = epoch_train_loss / len(train_loader)
train_acc = correct_train / total_train
# 驗證
model.eval()
correct_val = 0
total_val = 0
with torch.no_grad():
for images, labels in val_loader:
images, labels = images.to(device), labels.to(device).float().unsqueeze(1)
outputs = model(images)
preds = (outputs > 0.5).int()
correct_val += (preds == labels.int()).sum().item()
total_val += labels.size(0)
val_acc = correct_val / total_val
train_losses.append(avg_train_loss)
train_accuracies.append(train_acc)
val_accuracies.append(val_acc)
return train_losses, train_accuracies, val_accuracies
model_uniform = NeuralNetwork(init_type='uniform')
model_xavier = NeuralNetwork(init_type='xavier_output')
loss_uniform, train_acc_uniform, val_acc_uniform = train_model(model_uniform)
loss_xavier, train_acc_xavier, val_acc_xavier = train_model(model_xavier)
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.figure(figsize=(12,5))
plt.subplot(1,2,1)
plt.plot(loss_uniform, label='均勻初始化')
plt.plot(loss_xavier, label='Xavier輸出層初始化')
plt.title("訓練損失對比")
plt.xlabel("輪次(Epoch)")
plt.ylabel("損失")
plt.legend()
plt.grid(True)
plt.subplot(1,2,2)
plt.plot(train_acc_uniform, '--', label='訓練準確率-均勻')
plt.plot(val_acc_uniform, '-', label='驗證準確率-均勻')
plt.plot(train_acc_xavier, '--', label='訓練準確率-Xavier輸出層')
plt.plot(val_acc_xavier, '-', label='驗證準確率-Xavier輸出層')
plt.title("訓練/驗證準確率對比")
plt.xlabel("輪次(Epoch)")
plt.ylabel("準確率")
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
3.2 L2正則化部分完整代碼:
import torch
import torch.nn as nn
import torch.optim as optim
from torch.nn import init
from torchvision import datasets, transforms
from torch.utils.data import DataLoader, random_split
import matplotlib.pyplot as plt
transform = transforms.Compose([
transforms.Resize((128, 128)),
transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,))
])
dataset = datasets.ImageFolder(root='./cat_dog', transform=transform)
train_size = int(0.8 * len(dataset))
val_size = int(0.1 * len(dataset))
test_size = len(dataset) - train_size - val_size
train_dataset, val_dataset, test_dataset = random_split(dataset, [train_size, val_size, test_size])
train_loader = DataLoader(train_dataset, batch_size=32, shuffle=True)
val_loader = DataLoader(val_dataset, batch_size=32, shuffle=False)
test_loader = DataLoader(test_dataset, batch_size=32, shuffle=False)
class NeuralNetwork(nn.Module):
def __init__(self):
super().__init__()
self.flatten = nn.Flatten()
self.hidden1 = nn.Linear(128 * 128 * 3, 1024)
self.hidden2 = nn.Linear(1024, 512)
self.hidden3 = nn.Linear(512, 128)
self.hidden4 = nn.Linear(128, 32)
self.hidden5 = nn.Linear(32, 8)
self.hidden6 = nn.Linear(8, 3)
self.relu = nn.ReLU()
# 輸出層
self.output = nn.Linear(3, 1)
self.sigmoid = nn.Sigmoid()
# Xavier初始化輸出層
init.xavier_uniform_(self.output.weight)
def forward(self, x):
x = self.flatten(x)
x = self.relu(self.hidden1(x))
x = self.relu(self.hidden2(x))
x = self.relu(self.hidden3(x))
x = self.relu(self.hidden4(x))
x = self.relu(self.hidden5(x))
x = self.relu(self.hidden6(x))
x = self.sigmoid(self.output(x))
return x
model = NeuralNetwork()
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
model.to(device)
criterion = nn.BCELoss()
optimizer = optim.SGD(model.parameters(), lr=0.01,weight_decay=0.001)
epochs = 50
train_losses = []
train_accs = []
val_accuracies = []
for epoch in range(epochs):
model.train()
epoch_train_loss = 0
correct_train = 0
total_train = 0
for images, labels in train_loader:
images, labels = images.to(device), labels.to(device).float().unsqueeze(1)
outputs = model(images)
loss = criterion(outputs, labels)
optimizer.zero_grad()
loss.backward()
optimizer.step()
epoch_train_loss += loss.item()
preds = (outputs > 0.5).int()
correct_train += (preds == labels.int()).sum().item()
total_train += labels.size(0)
avg_train_loss = epoch_train_loss / len(train_loader)
train_acc = correct_train / total_train
train_losses.append(avg_train_loss)
train_accs.append(train_acc)
# 驗證
model.eval()
correct_val = 0
total_val = 0
with torch.no_grad():
for images, labels in val_loader:
images, labels = images.to(device), labels.to(device).float().unsqueeze(1)
outputs = model(images)
preds = (outputs > 0.5).int()
correct_val += (preds == labels.int()).sum().item()
total_val += labels.size(0)
val_acc = correct_val / total_val
val_accuracies.append(val_acc)
print(f"輪次: [{epoch + 1}/{epochs}], "
f"訓練損失: {avg_train_loss:.4f}, "
f"訓練準確率: {train_acc:.4f}, "
f"驗證準確率: {val_acc:.4f}")
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.figure(figsize=(10,5))
plt.plot(train_losses, label='訓練損失', color='tab:blue', linestyle='-')
plt.plot(train_accs, label='訓練準確率', color='tab:green', linestyle='--')
plt.plot(val_accuracies, label='驗證準確率', color='tab:red', linestyle='-.')
plt.title("訓練損失與訓練/驗證準確率隨輪次變化")
plt.xlabel("訓練輪次(Epoch)")
plt.ylabel("數值")
plt.legend()
plt.grid(True)
plt.show()
# 最終測試,可省略
model.eval()
correct = 0
total = 0
with torch.no_grad():
for images, labels in test_loader:
images, labels = images.to(device), labels.to(device).float().unsqueeze(1)
outputs = model(images)
preds = (outputs > 0.5).int()
correct += (preds == labels.int()).sum().item()
total += labels.size(0)
test_acc = correct / total
print(f"測試準確率: {test_acc:.4f}")
3.3 dropout正則化部分完整代碼:
import torch
import torch.nn as nn
import torch.optim as optim
from torch.nn import init
from torchvision import datasets, transforms
from torch.utils.data import DataLoader, random_split
import matplotlib.pyplot as plt
transform = transforms.Compose([
transforms.Resize((128, 128)),
transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,))
])
dataset = datasets.ImageFolder(root='./cat_dog', transform=transform)
train_size = int(0.8 * len(dataset))
val_size = int(0.1 * len(dataset))
test_size = len(dataset) - train_size - val_size
train_dataset, val_dataset, test_dataset = random_split(dataset, [train_size, val_size, test_size])
train_loader = DataLoader(train_dataset, batch_size=32, shuffle=True)
val_loader = DataLoader(val_dataset, batch_size=32, shuffle=False)
test_loader = DataLoader(test_dataset, batch_size=32, shuffle=False)
class NeuralNetwork(nn.Module):
def __init__(self):
super().__init__()
self.flatten = nn.Flatten()
self.hidden1 = nn.Linear(128 * 128 * 3, 1024)
self.hidden2 = nn.Linear(1024, 512)
self.hidden3 = nn.Linear(512, 128)
self.hidden4 = nn.Linear(128, 32)
self.hidden5 = nn.Linear(32, 8)
self.hidden6 = nn.Linear(8, 3)
self.relu = nn.ReLU()
# Dropout 層
self.dropout = nn.Dropout(p=0.4)
self.output = nn.Linear(3, 1)
self.sigmoid = nn.Sigmoid()
init.xavier_uniform_(self.output.weight)
def forward(self, x):
x = self.flatten(x)
x = self.relu(self.hidden1(x))
x = self.dropout(x)
x = self.relu(self.hidden2(x))
x = self.dropout(x)
x = self.relu(self.hidden3(x))
x = self.dropout(x)
x = self.relu(self.hidden4(x))
x = self.dropout(x)
x = self.relu(self.hidden5(x))
x = self.dropout(x)
x = self.relu(self.hidden6(x))
x = self.dropout(x)
x = self.sigmoid(self.output(x))
return x
model = NeuralNetwork()
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
model.to(device)
criterion = nn.BCELoss()
optimizer = optim.SGD(model.parameters(), lr=0.01)
epochs = 50
train_losses = []
train_accs = []
val_accuracies = []
for epoch in range(epochs):
model.train()
epoch_train_loss = 0
correct_train = 0
total_train = 0
for images, labels in train_loader:
images, labels = images.to(device), labels.to(device).float().unsqueeze(1)
outputs = model(images)
loss = criterion(outputs, labels)
optimizer.zero_grad()
loss.backward()
optimizer.step()
epoch_train_loss += loss.item()
preds = (outputs > 0.5).int()
correct_train += (preds == labels.int()).sum().item()
total_train += labels.size(0)
avg_train_loss = epoch_train_loss / len(train_loader)
train_acc = correct_train / total_train
train_losses.append(avg_train_loss)
train_accs.append(train_acc)
# 驗證
model.eval()
correct_val = 0
total_val = 0
with torch.no_grad():
for images, labels in val_loader:
images, labels = images.to(device), labels.to(device).float().unsqueeze(1)
outputs = model(images)
preds = (outputs > 0.5).int()
correct_val += (preds == labels.int()).sum().item()
total_val += labels.size(0)
val_acc = correct_val / total_val
val_accuracies.append(val_acc)
print(f"輪次: [{epoch + 1}/{epochs}], "
f"訓練損失: {avg_train_loss:.4f}, "
f"訓練準確率: {train_acc:.4f}, "
f"驗證準確率: {val_acc:.4f}")
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.figure(figsize=(10,5))
plt.plot(train_losses, label='訓練損失', color='tab:blue', linestyle='-')
plt.plot(train_accs, label='訓練準確率', color='tab:green', linestyle='--')
plt.plot(val_accuracies, label='驗證準確率', color='tab:red', linestyle='-.')
plt.title("訓練損失與訓練/驗證準確率隨輪次變化")
plt.xlabel("訓練輪次(Epoch)")
plt.ylabel("數值")
plt.legend()
plt.grid(True)
plt.show()
#最終測試,可省略
model.eval()
correct = 0
total = 0
with torch.no_grad():
for images, labels in test_loader:
images, labels = images.to(device), labels.to(device).float().unsqueeze(1)
outputs = model(images)
preds = (outputs > 0.5).int()
correct += (preds == labels.int()).sum().item()
total += labels.size(0)
test_acc = correct / total
print(f"測試準確率: {test_acc:.4f}")