此分類用於記錄吳恩達深度學習課程的學習筆記。
課程相關信息鏈接如下:
- 原課程視頻鏈接:[雙語字幕]吳恩達深度學習deeplearning.ai
- github課程資料,含課件與筆記:吳恩達深度學習教學資料
- 課程配套練習(中英)與答案:吳恩達深度學習課後習題與答案
本週為第二課的第二週內容,2.1和2.2的內容。
本週為第二課的第二週內容,和題目一樣,本週的重點是優化算法,即如何更好,更高效地更新參數幫助擬合的算法,還是離不開那句話:優化的本質是數學。
因此,在理解上,本週的難道要相對較高一些,公式的出現也會更加頻繁。
當然,我仍會補充一些更基礎的內容來讓理解的過程更絲滑一些。
本篇的內容關於Mini-batch 梯度下降,是對之前梯度下降的補充和完善。
1. Mini-batch 梯度下降法
其實我們早就在使用這個方法了,現在來系統的闡述一下。
如果你有些遺忘了梯度下降法本身的概念,可以回看之前的筆記:梯度下降法
而發展出的隨機梯度,Mini-batch 梯度,batch 梯度只是一次迭代中使用樣本數量的不同。
1.1 隨機梯度下降法
實際上,在第一週學習向量化之前,我們理解的梯度下降法就是隨機梯度下降法(Stochastic Gradient Descent,SGD)。
具體展開概念:
隨機梯度下降法是一種優化算法,常用於訓練機器學習模型,尤其是在深度學習中。隨機梯度下降法在每次更新時只使用一個樣本來計算梯度並進行參數更新,而與之相對的批量梯度下降法,就是使用全部樣本計算梯度並更新。
也就是説,在一次訓練中,我們有多少個樣本,就會進行多少次參數更新。
現在展開幾個小問題。
(1)使用隨機梯度下降和是否向量化的關係?
之前在向量化部分我們提到,使用向量化是為了在代碼中避免顯示的for循環,以並行提高效率。
通過向量化,我們可以並行地進行多個樣本的訓練,用多個樣本的損失更新參數。
那現在使用隨機梯度下降,我們一次迭代只用一個樣本,那是不是就代表我們要使用非向量化的輸入?
先説結論:隨機梯度下降 ≠ 非向量化,因為 “是否向量化” 和 “是否使用隨機梯度” 是兩個不同維度的問題:
- 向量化 → 指的是代碼實現方式(是否用for循環逐樣本計算)。
- SGD / Mini-batch / Batch GD → 指的是算法在每次更新參數時使用多少樣本。
也就是説:
我們完全可以向量化地實現SGD,即一次用一個樣本,但仍然用矩陣操作計算,二者可以並存。
舉個例子:
就像做飯時,“你一次炒幾份菜”與“你用不用電磁爐這種高效設備”是兩件不同的事情。
是否向量化,就像是你用不用電磁爐、用不用多頭灶台,它決定的是你做菜的效率,是工具層面的提升。
而隨機梯度下降、Batch 或 Mini-batch 則是你每次炒幾人份:一次炒一份、一次炒十份、還是一次炒滿整鍋,這是做飯方式的選擇。
你完全可以同時做到“使用電磁爐(向量化)”並且“每次只炒一份(SGD)”。兩者互不矛盾,只是一個管“快不快”,一個管“每次做多少”。
這就是二者的區別。
(2)隨機梯度下降的優劣?
先總地看一下這個算法的優劣:
| SGD 的特點 | 它帶來的優點 | 它造成的缺點 |
|---|---|---|
| 每次只使用 1 個樣本更新(高頻、小步、噪聲大) | 更新非常頻繁,模型能更快開始學習;帶噪聲的更新更容易跳出局部最優 | 噪聲過大導致收斂不穩定;損失曲線抖動明顯;學習率一旦偏大容易發散 |
| 每次計算量小(佔用內存少) | 不需要大顯存,小設備也能訓練;適合超大規模數據 | 單次處理數據量太小,無法用好 GPU 的並行能力,整體訓練速度反而偏慢 |
| 更新方向依賴單一樣本(信息量少) | 每次更新成本低,可以快速迭代 | 單一樣本可能不能代表整體趨勢,更新方向偏差大,需要更多 epoch 才能收斂 |
對於其中第一點可能不太清晰,我們來詳細解釋一下。
(3)SGD的收斂不穩定現象
我們剛剛提到,“每次只使用一個樣本更新”會帶來一個核心影響:更新方向帶有更多的噪聲。
為了更好的理解這點,我們依舊把最小化損失類比成從山谷下山。
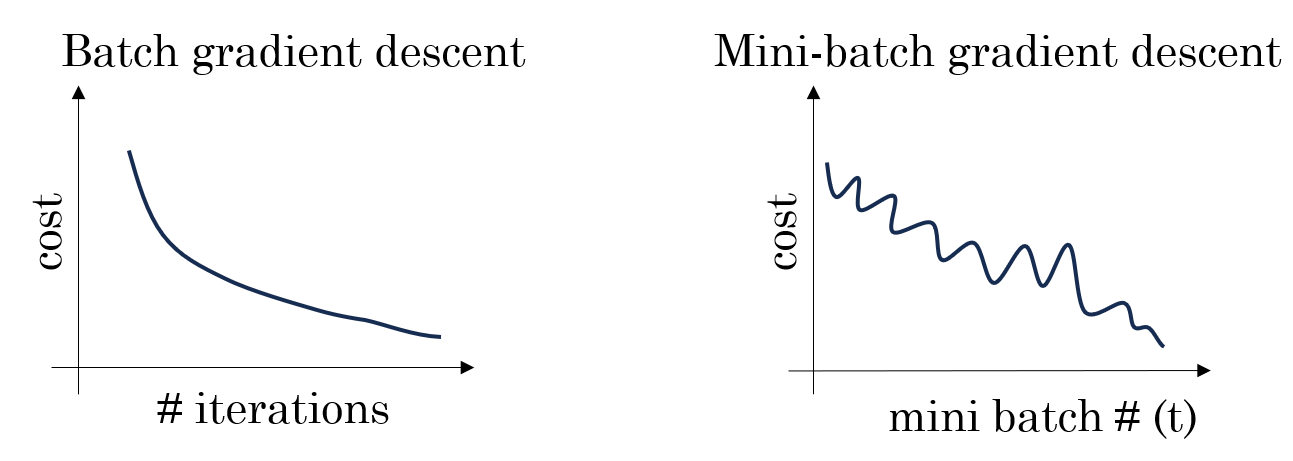
如果我們使用批量梯度下降(Batch GD),每次更新方向是所有樣本平均後的梯度,因此方向非常穩定,像是沿着山谷中心線穩穩地往下走。
但 SGD 不同。因為它每次只使用一個樣本,如果這個樣本是個“好樣本”,那更新後損失就向谷底走一步,如果下一個樣本是噪聲樣本,更新後損失甚至可能回反着走回去。這樣每次更新對單一樣本的依賴就會帶來損失的“振盪”,導致收斂不穩定,就像一個不準的導航,讓你繞着彎下山。
1.2 Mini-batch 梯度下降法
Mini-batch 梯度下降法是介於Batch GD和SGD之間的一種折中方案。它每次更新使用一個小批量樣本,而不是全部樣本或單個樣本。
舉個實例,假設我們有 1000 個樣本,設置 mini-batch 大小為 10,那麼每次迭代我們會隨機選 10 個樣本計算平均梯度,並更新參數,這樣下來,一個 epoch 需要進行 (1000 / 10 = 100) 次參數更新。
(1)Mini-batch 的優缺點
| Mini-batch 特點 | 它帶來的優點 | 它造成的缺點 |
|---|---|---|
| 每次使用部分樣本更新 | 更新方向比 SGD 穩定,損失曲線波動小,收斂更可靠 | 每次更新仍存在一定噪聲,收斂路徑不是完全平滑 |
| 計算量適中,可利用並行 | 可以充分利用 GPU 並行能力,訓練速度快 | mini-batch 太小會像 SGD 一樣噪聲大,太大又趨向 Batch GD,靈活性降低 |
| 在噪聲和穩定性之間折中 | 既有一定跳出局部最優的能力,又不會像 SGD 那樣過於顛簸 | 超參數(batch size)需要調節,不同任務最優值不同 |
(2)Mini-batch 的收斂表現
在“下山”比喻下,Mini-batch 就像是手裏拿着局部準確的地圖:
- 噪聲被部分平滑:每次看幾個人的樣本,方向不會因為單一樣本異常而大幅偏離。
- 路徑仍有微小抖動:相比 Batch GD,仍然可以“微調”路線,更靈活地適應複雜地形。
- 訓練效率較高:每次更新佔用內存適中,可以充分利用 GPU 並行,整體訓練時間比 SGD 更短。
總的來説,Mini-batch 在性能和成本上的平衡讓其成為了我們的最佳選擇。
但Mini-batch也帶來一個新的超參數:批次大小(Batch size)。
(3)Batch size 的選擇
Mini-batch 的核心超參數是 batch size,一般來説:
- 小 batch(如 1~32) → 噪聲大,收斂不穩定,但可能幫助跳出局部最優
- 中 batch(如 64~256) → 收斂穩定,訓練速度較快,適合大部分任務
- 大 batch(如 1024 以上) → 接近 Batch GD,收斂平穩,但對 GPU 顯存要求高
因此,我們通常的選擇是這樣的: - 小數據集 → 可用大 batch,保證穩定收斂
- 大數據集 → 使用中等 batch,兼顧效率與穩定性
- 儘量避免過小或過大的批次大小。