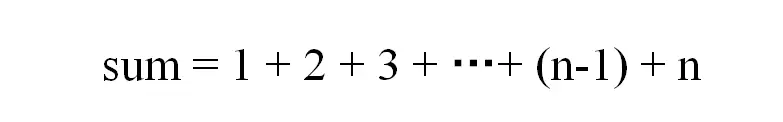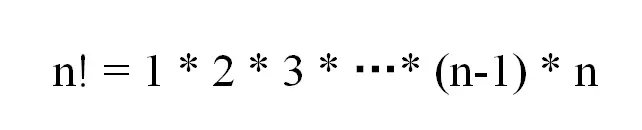1. 示例
週末你帶着TA去電影院看電影,TA問你,咱們現在坐在第幾排啊?電影院裏面太黑了,看不清,沒法數,現在你怎麼辦?
這時可以這樣操作:問前一排的,他是第幾排。前一排的不知道自己是第幾排,繼續向前問。直到第一排,由於他面對着屏幕,知道自己是第一排。之後再給後面的回話:“我是第一排”,後面的知道了前面的,也就知道了自己的(在前面的基礎上+1)。之後再給後面的回覆。
2. 遞歸條件
3. 應用
應用1:求解1到n的和
如果要求解sum(n),假如已經知道了sum(n-1),就可以知道sum(n)了。因為sum(n)=sum(n-1)+n。因此求解思路可以是:
求解sum(n),需要知道sum(n-1);求解sum(n-1)需要知道sum(n-2) ... 一直到sum(1),這時sum(1)==1是已知的。這完全符合遞歸的思想:先遞過去,再歸回來。
應用2:求解n的階乘
如果要求解n!,假如已經知道了(n-1)!,就可以知道n!了。因為n!=(n-1) x n。因此求解思路可以是:
求解n!,需要知道n(-1)!;求解(n-1)!需要知道(n-2)! ... ,一直到1!,這時1!==1是已知的。這完全符合遞歸的思想:先遞過去,再歸回來。
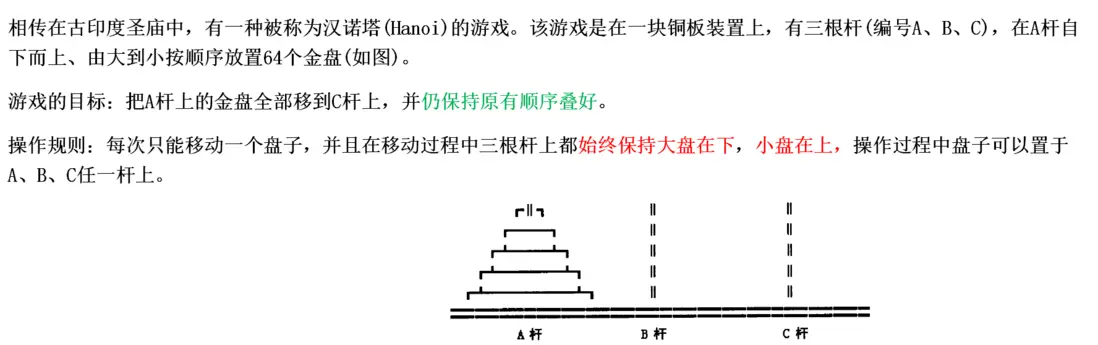
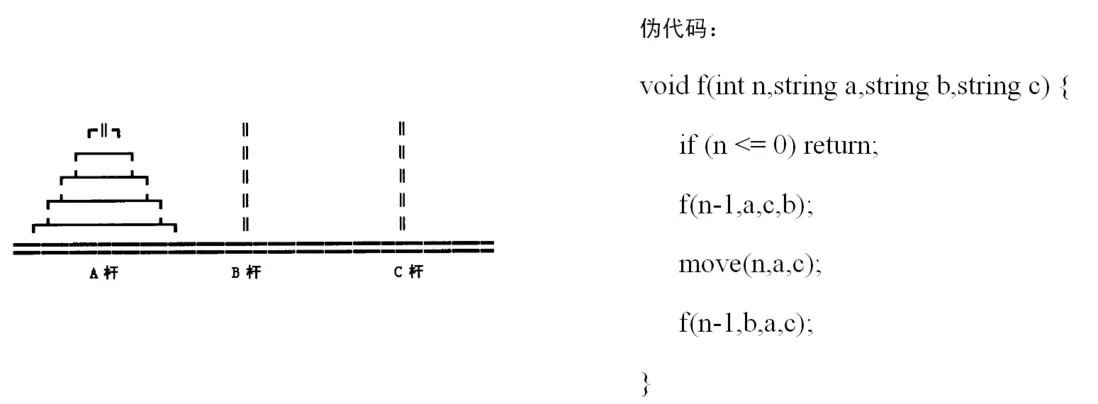
應用3:漢諾塔問題
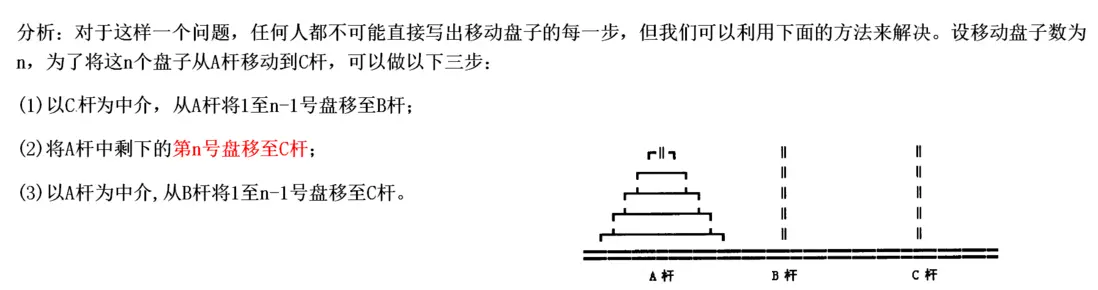
在上述過程只,將1至n-1號盤子看為一個整體來處理的。而對於1至n-1號盤子的處理方法同樣可以按照以上步驟進行。1至n-2號盤子的處理方法也是同樣的,直到沒有需要處理的盤子截止(n<=0)。
這完全符合遞歸的思路:
4. 小結
如果文字描述的不太清楚,你可以參考視頻的詳細講解。
- Python版本:https://www.bilibili.com/cheese/play/ep1371217
- Java版本:https://www.bilibili.com/cheese/play/ep1367103
- Golang版本:https://www.bilibili.com/cheese/play/ep1364643