機械臂路徑規劃深度學習模型詳情 - 機械臂路徑規劃深度學習模型,機械臂,舵機,define,深度學習,人工智能 bugouhen 博客

二連桿機械臂角度解算

本文采用極座標的平移變換公式或者餘弦定理的方法在定座標點的情況下去解算二連桿機械臂兩個關節處應該旋轉的角度。由於餘弦定理更容易理解且極座標的平移變換公式和餘弦定理推導出來的角度解算結果公式一致，接下來會用餘弦定理去推導最終公式。

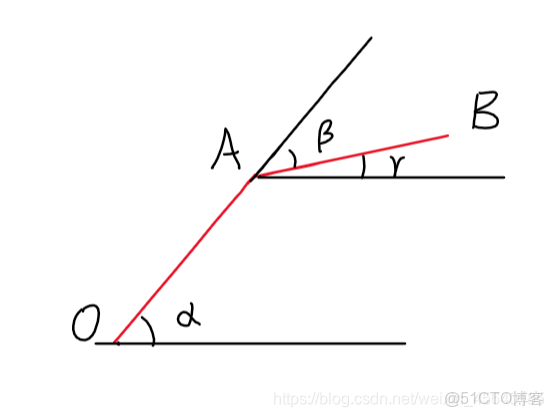
我們要解決的問題是已知一個目標點座標(x，y)，已知兩個連桿的長度OA，AB，我們的目標是求α和β這兩個關節角。如下圖所示：

機械臂路徑規劃深度學習模型_機械臂路徑規劃深度學習模型

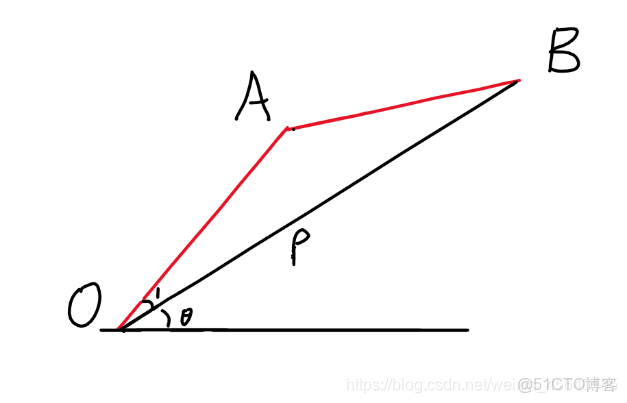
根據同位角關係可知β=α-γ，所以我們只需要求出角α和角γ即可。角α可分為角1和角θ相加。

機械臂路徑規劃深度學習模型_機械臂_02

由於B點座標已經給出，由機械臂路徑規劃深度學習模型_機械臂_03 可求出角θ，角1由余弦定理機械臂路徑規劃深度學習模型_舵機_04 可得

機械臂路徑規劃深度學習模型_舵機_05

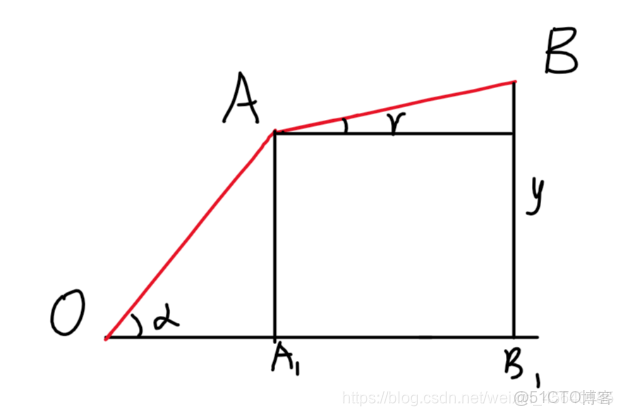
由於B點縱座標y=OAsin⁡α+ABsin⁡γ。角α已知y已知，可求角γ。由於β=α-γ，角β可求。

下面給出具體C語言代碼（代碼中的角度全部都是弧度制）：

#define L1 105.0f
#define L2 145.0f    //此處L1，L2為上文的OA和AB
#define LIMIT(x,min,max) (x)=(((x)<=(min))?(min):(((x)>=(max))?(max):(x)))
//座標系
typedef struct
{
	int16_t x;
	int16_t y;
	int32_t sqr_rho;
	float rho;
	float theta;
}Coordinate;

typedef struct
{
	float alpha;
	float beta;
}MchArmAngle;


//直角座標轉為極座標
void CordTF(Coordinate* cord , int16_t x , int16_t y)
{
	cord->x = x;
	cord->y = y;
	cord->sqr_rho = x*x + y*y;
	cord->rho = sqrt((float)cord->sqr_rho);
	cord->theta = (float)atan2((double)y,(double)x);
}

//機械臂角度解算
void AngleCalc(MchArmAngle* angle,Coordinate* cord)
{
	if((cord->sqr_rho<(L1+L2)*(L1+L2))&&(cord->sqr_rho>(L1-L2)*(L1-L2)))
	{
		float temp1,temp2;
		temp1 = (cord->sqr_rho + L1*L1 - L2*L2)/(2*L1*cord->rho);
		angle->alpha = cord->theta + acos(temp1); //此處的加號是下文提到的加號
		temp2 = ((float)cord->y - L1*sin(angle->alpha))/L2;
		angle->beta = asin(temp2) - angle->alpha + PI/2.0f;
		LIMIT(angle->alpha,0,PI);
		LIMIT(angle->beta,0,PI);
	}
	return;
}

CordTF這個函數意義主要是計算出OB和角θ。由於OB和角θ相當於B點的極座標，所以函數叫座標變換。

AngleCalc函數if是因為假如機械臂兩個關節是可以360度旋轉的，那麼B點可以到的範圍就是一個圓環，加入這個if就是防止人為輸入一個機械臂不可能達到的點，導致角度解算出一個NAN值。

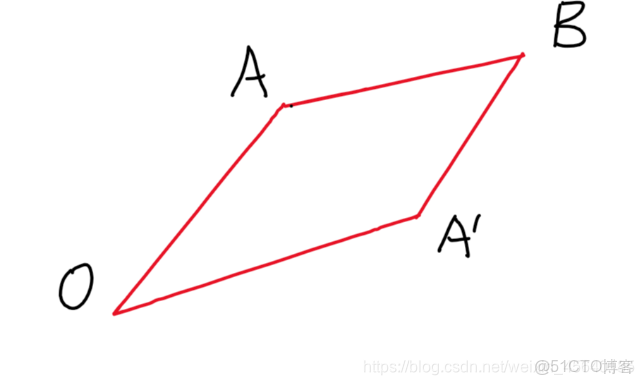
細心的同學可能發現了在計算角α的時候有一個用到了一個acos，我們都知道cos是一個偶函數，所以其實在解算過程中到達指定座標的角度其實是兩組值，如圖所示：

機械臂路徑規劃深度學習模型_#define_06