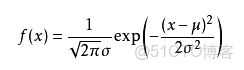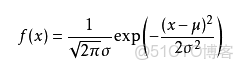極大似然估計，通俗理解來説，就是利用已知的樣本結果信息，反推最具有可能（最大概率）導致這些樣本結果出現的模型參數值！

換句話説，極大似然估計提供了一種給定觀察數據來評估模型參數的方法，即：“模型已定，參數未知”。

可能有小夥伴就要説了，還是有點抽象呀。我們這樣想，一當模型滿足某個分佈，它的參數值我通過極大似然估計法求出來的話。比如正態分佈中公式如下：

現在真要先講講MLE了。。

例子一

別人博客的一個例子。

假如有一個罐子，裏面有黑白兩種顏色的球，數目多少不知，兩種顏色的比例也不知。我 們想知道罐中白球和黑球的比例，但我們不能把罐中的球全部拿出來數。現在我們可以每次任意從已經搖勻的罐中拿一個球出來，記錄球的顏色，然後把拿出來的球 再放回罐中。這個過程可以重複，我們可以用記錄的球的顏色來估計罐中黑白球的比例。假如在前面的一百次重複記錄中，有七十次是白球，請問罐中白球所佔的比例最有可能是多少？

很多人馬上就有答案了：70%。而其後的理論支撐是什麼呢？

所以每次抽出來的球的顏 色服從同一獨立分佈。

這裏我們把一次抽出來球的顏色稱為一次抽樣。題目中在一百次抽樣中，七十次是白球的,三十次為黑球事件的概率是P(樣本結果|Model)。

如果第一次抽象的結果記為x1,第二次抽樣的結果記為x2....那麼樣本結果為(x1,x2.....,x100)。這樣，我們可以得到如下表達式：

P(樣本結果|Model)

　　= P(x1,x2,…,x100|Model)

　　= P(x1|Mel)P(x2|M)…P(x100|M)

　　= p^70(1-p)^30.

好的，我們已經有了觀察樣本結果出現的概率表達式了。那麼我們要求的模型的參數，也就是求的式中的p。

那麼我們怎麼來求這個p呢？

不同的p，直接導致P（樣本結果|Model）的不同。

好的，我們的p實際上是有無數多種分佈的。如下：

那麼求出 p^70(1-p)^30為 7.8 * 10^(-31)

p的分佈也可以是如下：

那麼也可以求出p^70(1-p)^30為2.95* 10^(-27)

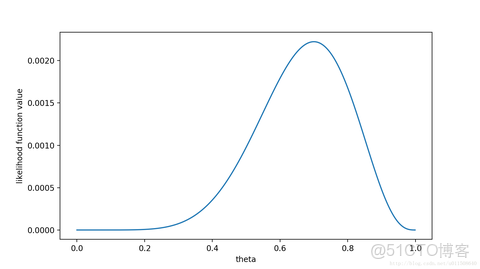
那麼問題來了，既然有無數種分佈可以選擇，極大似然估計應該按照什麼原則去選取這個分佈呢？

答：採取的方法是讓這個樣本結果出現的可能性最大，也就是使得p^70(1-p)^30值最大，那麼我們就可以看成是p的方程，求導即可！

那麼既然事情已經發生了，為什麼不讓這個出現的結果的可能性最大呢？這也就是最大似然估計的核心。

我們想辦法讓觀察樣本出現的概率最大，轉換為數學問題就是使得：

p^70(1-p)^30最大，這太簡單了，未知數只有一個p，我們令其導數為0，即可求出p為70%，與我們一開始認為的70%是一致的。其中藴含着我們的數學思想在裏面。

例子二

假設我們要統計全國人民的年均收入，首先假設這個收入服從服從正態分佈，但是該分佈的均值與方差未知。我們沒有人力與物力去統計全國每個人的收入。我們國家有10幾億人口呢？那麼豈不是沒有辦法了？

不不不，有了極大似然估計之後，我們可以採用嘛！我們比如選取一個城市，或者一個鄉鎮的人口收入，作為我們的觀察樣本結果。然後通過最大似然估計來獲取上述假設中的正態分佈的參數。

有了參數的結果後，我們就可以知道該正態分佈的期望和方差了。也就是我們通過了一個小樣本的採樣，反過來知道了全國人民年收入的一系列重要的數學指標量！

那麼我們就知道了極大似然估計的核心關鍵就是對於一些情況，樣本太多，無法得出分佈的參數值，可以採樣小樣本後，利用極大似然估計獲取假設中分佈的參數值。

希望對您理解有幫助~