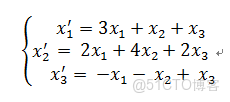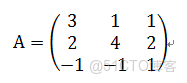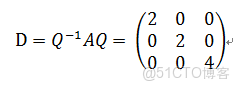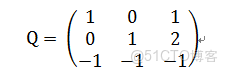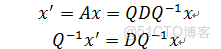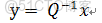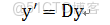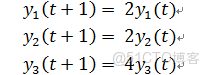如何理解矩陣特徵值？
想要理解特徵值，首先要理解矩陣相似。什麼是矩陣相似呢？從定義角度就是：存在可逆矩陣P滿足B＝
則我們説A和B是相似的。讓我們來回顧一下之前得出的重要結論：對於同一個線性空間，可以用兩組不同的基
和基
來描述，他們之間的過渡關係是這樣的：
，而對應座標之間的過渡關係是這樣的：
。其中P是可逆矩陣，可逆的意義是我們能變換過去也要能變換回來，這一點很重要。
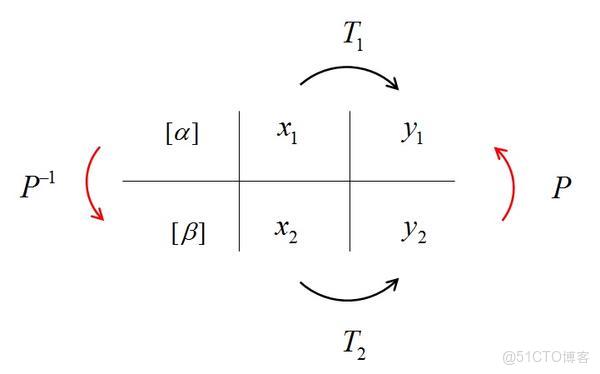
我們知道，對於一個線性變換，只要你選定一組基，那麼就可以用一個矩陣T1來描述這個線性變換。換一組基，就得到另一個不同的矩陣T2（之所以會不同，是因為選定了不同的基，也就是選定了不同的座標系）。所有這些矩陣都是這同一個線性變換的描述，但又都不是線性變換本身。具體來説，有一個線性變換
，我們選擇基
來描述，對應矩陣是
；同樣的道理，我們選擇基
來描述
，，對應矩陣是
；我們知道基
和基
是有聯繫的，那麼他們之間的變換
和
有沒有聯繫呢？
當然有，
和
就是相似的關係，具體的請看下圖：
沒錯，所謂相似矩陣，就是同一個線性變換的不同基的描述矩陣。這就是相似變換的幾何意義。
這個發現太重要了。原來一族相似矩陣都是同一個線性變換的描述啊！難怪這麼重要！工科研究生課程中有矩陣論、矩陣分析等課程，其中講了各種各樣的相似變換，比如什麼相似標準型，對角化之類的內容，都要求變換以後得到的那個矩陣與先前的那個矩陣式相似的，為什麼這麼要求？因為只有這樣要求，才能保證變換前後的兩個矩陣是描述同一個線性變換的。就像信號處理（積分變換）中將信號（函數）進行拉氏變換，在複數域處理完了之後又進行拉式反變換，回到實數域一樣。信號處理中是主要是為了將複雜的卷積運算變成乘法運算。其實這樣的變換還有好多，有興趣可以看積分變換的教材。
為什麼這樣做呢？矩陣的相似變換可以把一個比較醜的矩陣變成一個比較美的矩陣，而保證這兩個矩陣都是描述了同一個線性變換。至於什麼樣的矩陣是“美”的，什麼樣的是“醜”的，我們説對角陣是美的。在線性代數中，我們會看到，如果把複雜的矩陣變換成對角矩陣，作用完了之後再變換回來，這種轉換很有用處，比如求解矩陣的n次冪！而學了矩陣論之後你會發現，矩陣的n次冪是工程中非常常見的運算。這裏順便説一句，將矩陣對角化在控制工程和機械振動領域具有將複雜方程解耦的妙用！總而言之，相似變換是為了簡化計算！
從另一個角度理解矩陣就是：矩陣主對角線上的元素表示自身和自身的關係，其他位置的元素aij表示i位置和j位置元素之間的相互關係。那麼好，特徵值問題其實就是選取了一組很好的基，就把矩陣 i位置和j位置元素之間的相互關係消除了。而且因為是相似變換，並沒有改變矩陣本身的特性。因此矩陣對角化才如此的重要！
特徵向量的引入是為了選取一組很好的基。空間中因為有了矩陣，才有了座標的優劣。對角化的過程，實質上就是找特徵向量的過程。如果一個矩陣在複數域不能對角化，我們還有辦法把它化成比較優美的形式——Jordan標準型。高等代數理論已經證明：一個方陣在複數域一定可以化成Jordan標準型。這一點有興趣的同學可以看一下高等代數後或者矩陣論。
經過上面的分析相信你已經可以得出如下結論了：座標有優劣，於是我們選取特徵向量作為基底，那麼一個線性變換最核心的部分就被揭露出來——當矩陣表示線性變換時，特徵值就是變換的本質！特徵值的幾何意義前面的答主已經用很多圖解釋過了，接下來我們分析一下特徵值的物理意義：特徵值英文名eigen value。“特徵”一詞譯自德語的eigen，由希爾伯特在1904年首先在這個意義下使用（赫爾曼·馮·亥姆霍茲在更早的時候也在類似意義下使用過這一概念）。eigen一詞可翻譯為“自身的”，“特定於...的”，“有特徵的”或者“個體的”—這強調了特徵值對於定義特定的變換上是很重要的。它還有好多名字，比如譜，本徵值。為什麼會有這麼多名字呢？
原因就在於他們應用的領域不同，中國人為了區分，給特不同的名字。你看英文文獻就會發現，他們的名字都是同一個。當然，特徵值的思想不僅僅侷限於線性代數，它還延伸到其他領域。在數學物理方程的研究領域，我們就把特徵值稱為本徵值。如在求解薛定諤波動方程時，在波函數滿足單值、有限、連續性和歸一化條件下，勢場中運動粒子的總能量(正)所必須取的特定值，這些值就是正的本徵值。
前面我們討論特徵值問題面對的都是有限維度的特徵向量，下面我們來看看特徵值對應的特徵向量都是無限維函數的例子。這時候的特徵向量我們稱為特徵函數，或者本證函數。這還要從你熟悉的微分方程説起。方程本質是一種約束，微分方程就是在世界上各種各樣的函數中，約束出一類函數。對於一階微分方程
我們發現如果我將變量y用括號[]包圍起來，微分運算的結構和線性代數中特徵值特徵向量的結構,即
和
竟是如此相似。這就是一個求解特徵向量的問題啊！只不過“特徵向量”變成函數！我們知道只有
滿足這個式子。這裏出現了神奇的數e，一杯開水放在室內，它温度的下降是指數形式的；聽説過放射性元素的原子核發生衰變麼？隨着放射的不斷進行，放射強度將按指數曲線下降；化學反應的進程也可以用指數函數描述……類似的現象還有好多。
為什麼選擇指數函數而不選擇其他函數，因為指數函數是特徵函數。為什麼指數函數是特徵？我們從線性代數的特徵向量的角度來解釋。這已經很明顯了
就是“特徵向量”。於是，很自然的將線性代數的理論應用到線性微分方程中。那麼指數函數就是微分方程（實際物理系統）的特徵向量。用特徵向量作為基表示的矩陣最為簡潔。就像你把一個方陣經過相似對角化變換，耦合的矩陣就變成不耦合的對角陣一樣。在機械振動裏面所説的模態空間也是同樣的道理。如果你恰巧學過振動分析一類的課程，也可以來和我交流。
同理，用特徵函數解的方程也是最簡潔的，不信你用級數的方法解方程，你會發現方程的解有無窮多項。解一些其他方程的時候(比如貝塞爾方程)我們目前沒有找到特徵函數，於是退而求其次才選擇級數求解，至少級數具有完備性。實數的特徵值代表能量的耗散或者擴散，比如空間中熱量的傳導、化學反應的擴散、放射性元素的衰變等。虛數的特徵值(對應三角函數)代表能量的無損耗交換，比如空間中的電磁波傳遞、振動信號的動能勢能等。複數的特徵值代表既有交換又有耗散的過程，實際過程一般都是這樣的。復特徵值在電路領域以及振動領域將發揮重要的作用，可以説，沒有複數，就沒有現代的電氣化時代！
對於二階微分方程方程，它的解都是指數形式或者復指數形式。可以通過歐拉公式將其寫成三角函數的形式。復特徵值體現最多的地方是在二階系統，別小看這個方程，整本自動控制原理都在講它，整個振動分析課程也在講它、還有好多課程的基礎都是以這個微分方程為基礎，這裏我就不詳細説了，有興趣可以學習先關課程。説了這麼多隻是想向你傳達一個思想，就是復指數函數式系統的特徵向量！
如果將二階微分方程轉化成狀態空間
的形式(具體轉化方法見現代控制理論，很簡單的)
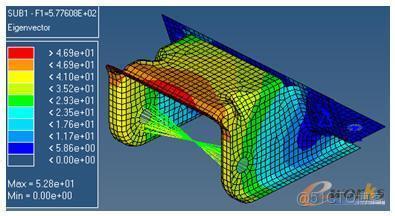
。則一個二階線性微分方程就變成一個微分方程組的形式這時就出現了矩陣A，矩陣可以用來描述一個系統：如果是振動問題，矩陣A的特徵值是虛數，對應系統的固有頻率，也就是我們常説的，特徵值代表振動的譜。如果含有耗散過程，特徵值是負實數，對應指數衰減；特徵值是正實數，對應指數發散過程，這時是不穩定的，説明系統極容易崩潰，如何抑制這種發散就是控制科學研究的內容。
提到振動的譜，突然想到了這個經典的例子：美國數學家斯特讓（G..Strang）在其經典教材《線性代數及其應用》中這樣介紹了特徵值作為頻率的物理意義，他説："大概最簡單的例子（我從不相信其真實性，雖然據説1831年有一橋樑毀於此因）是一對士兵通過橋樑的例子。傳統上，他們要停止齊步前進而要散步通過。這個理由是因為他們可能以等於橋的特徵值之一的頻率齊步行進，從而將發生共振。就像孩子的鞦韆那樣，你一旦注意到一個鞦韆的頻率，和此頻率相配，你就使頻率蕩得更高。一個工程師總是試圖使他的橋樑或他的火箭的自然頻率遠離風的頻率或液體燃料的頻率；而在另一種極端情況，一個證券經紀人則盡畢生精力於努力到達市場的自然頻率線。特徵值是幾乎任何一個動力系統的最重要的特徵。"
對於一個線性系統，總可以把高階的方程轉化成一個方程組描述，這被稱為狀態空間描述。因此，他們之間是等價的。特徵值還有好多用處，原因不在特徵值本身，而在於特徵值問題和你的物理現象有着某種一致的對應關係。學習特徵值問題告訴你一種解決問題的方法：尋找事物的特徵，然後特徵分解。
最後聲明一下， 本文是在整理孟巖老師的《理解矩陣》和任廣千、胡翠芳老師的《線性代數的幾何意義》基礎上形成的，只是出於一種對數學的愛好！有興趣的讀者建議閲讀原文。也歡迎下載《神奇的矩陣》和《神奇的矩陣第二季》瞭解更多有關線性代數和矩陣的知識。
補充：答主現在用到的多數是對稱矩陣或酉矩陣的情況，有思維定勢了，寫了半天才發現主要講的是對稱矩陣，這答案就當科普用了。特徵值在很多領域應該都有自己的用途，它的物理意義到了本科高年級或者研究生階段涉及到具體問題的時候就容易理解了，剛學線性代數的話，確實抽象。
——————————————————以下為正文——————————————————
從線性空間的角度看，在一個定義了內積的線性空間裏，對一個N階對稱方陣進行特徵分解，就是產生了該空間的N個標準正交基，然後把矩陣投影到這N個基上。N個特徵向量就是N個標準正交基，而特徵值的模則代表矩陣在每個基上的投影長度。
特徵值越大，説明矩陣在對應的特徵向量上的方差越大，功率越大，信息量越多。
應用到最優化中，意思就是對於R的二次型，自變量在這個方向上變化的時候，對函數值的影響最大，也就是該方向上的方向導數最大。
應用到數據挖掘中，意思就是最大特徵值對應的特徵向量方向上包含最多的信息量，如果某幾個特徵值很小，説明這幾個方向信息量很小，可以用來降維，也就是刪除小特徵值對應方向的數據，只保留大特徵值方向對應的數據，這樣做以後數據量減小，但有用信息量變化不大。
——————————————————舉兩個栗子——————————————————
應用1 二次型最優化問題
二次型
，其中R是已知的二階矩陣，R=[1，0.5；0.5，1]，x是二維列向量，x=[x1；x2]，求y的最小值。求解很簡單，講一下這個問題與特徵值的關係。
對R特徵分解，特徵向量是[-0.7071；0.7071]和[0.7071；0.7071]，對應的特徵值分別是0.5和1.5。
然後把y的等高線圖畫一下
從圖中看，函數值變化最快的方向，也就是曲面最陡峭的方向，歸一化以後是[0.7071；0.7071]，嗯哼，這恰好是矩陣R的一個特徵值，而且它對應的特徵向量是最大的。因為這個問題是二階的，只有兩個特徵向量，所以另一個特徵向量方向就是曲面最平滑的方向。這一點在分析最優化算法收斂性能的時候需要用到。
二階問題比較直觀，當R階數升高時，也是一樣的道理。
應用2 數據降維
興趣不大的可以跳過問題，直接看後面降維方法。
機器學習中的分類問題，給出178個葡萄酒樣本，每個樣本含有13個參數，比如酒精度、酸度、鎂含量等，這些樣本屬於3個不同種類的葡萄酒。任務是提取3種葡萄酒的特徵，以便下一次給出一個新的葡萄酒樣本的時候，能根據已有數據判斷出新樣本是哪一種葡萄酒。
問題詳細描述：UCI Machine Learning Repository: Wine Data Set訓練樣本數據：http://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data
原數據有13維，但這之中含有冗餘，減少數據量最直接的方法就是降維。
做法：把數據集賦給一個178行13列的矩陣R，減掉均值並歸一化，它的協方差矩陣
，C是13行13列的矩陣，對C進行特徵分解，對角化
，其中U是特徵向量組成的矩陣，D是特徵之組成的對角矩陣，並按由大到小排列。然後，另
，就實現了數據集在特徵向量這組正交基上的投影。嗯，重點來了，R’中的數據列是按照對應特徵值的大小排列的，後面的列對應小特徵值，去掉以後對整個數據集的影響比較小。比如，現在我們直接去掉後面的7列，只保留前6列，就完成了降維。這個降維方法叫PCA（Principal Component Analysis）。
下面看結果：
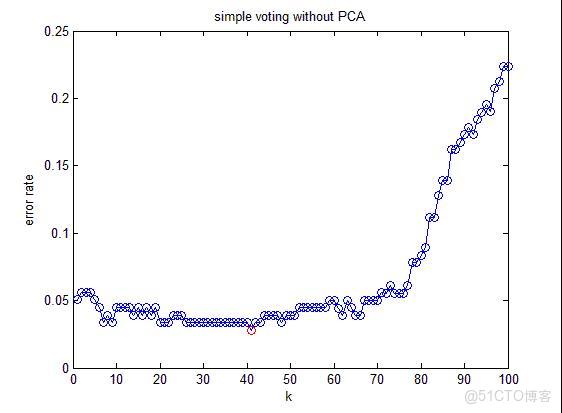
這是不降維時候的分類錯誤率。
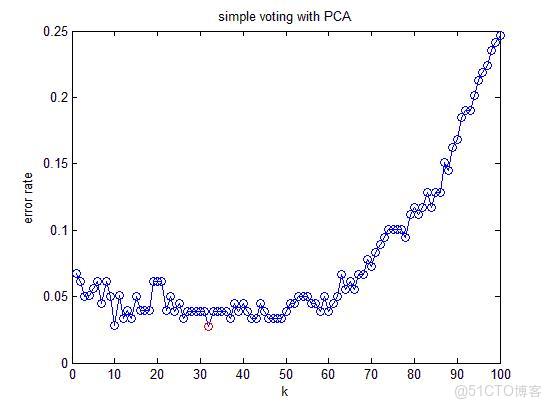
這是降維以後的分類錯誤率。
特徵值不僅僅是數學上的一個定義或是工具，特徵值是有具體含義的，是完全看得見摸得着的。
1. 比如説一個三維矩陣，理解成線性變換，作用在一個球體上：
三個特徵值決定了 對球體在三個維度上的拉伸/壓縮，把球體塑造成一個橄欖球；
剩下的部分決定了這個橄欖球在三維空間裏面怎麼旋轉。
2. 對於一個微分方程：
將係數提取出來
對角化：
其中
由於
定義
於是有
因此y的變化率與特徵值息息相關：
再將y由Q變換回x，我們就能得出x在不同時間的值。x的增長速度就是特徵值λ，Q用來把x旋轉成y。
我們知道，一張圖像的像素（如:320 x 320）到了計算機裏面事實上就是320x320的矩陣，每一個元素都代表這個像素點的顏色..
如果我們把基於特徵值的應用，如PCA、向量奇異值分解SVD這種東西放到圖像處理上，大概就可以提供一個看得到的、直觀的感受。關於SVD的文章可以參考LeftNotEasy的文章：機器學習中的數學(5)-強大的矩陣奇異值分解(SVD)及其應用
簡單的説，SVD的效果就是..用一個規模更小的矩陣去近似原矩陣...
這裏A就是代表圖像的原矩陣..其中的
尤其值得關注，它是由A的特徵值從大到小放到對角線上的..也就是説，我們可以選擇其中的某些具有“代表性”的特徵值去近似原矩陣！左邊的是原始圖片
當我把特徵值的數量減少幾個的時候...後面的圖像變“模糊”了..
同樣地...
關鍵的地方來了！如果我們只看到這裏的模糊..而沒有看到計算機（或者説數學）對於人臉的描述，那就太可惜了...我們看到，不論如何模糊，臉部的關鍵部位（我們人類認為的關鍵部位）——五官並沒有變化太多...這能否説：數學揭示了世界的奧秘？
前面的回答比較專業化，而且好像沒説特徵值是虛數的情況，並不是只有特徵向量的伸縮。作為工科線代水平，我説下自己的理解。
矩陣特徵值是對特徵向量進行伸縮和旋轉程度的度量，實數是隻進行伸縮，虛數是隻進行旋轉，複數就是有伸縮有旋轉。其實最重要的是特徵向量，從它的定義可以看出來，特徵向量是在矩陣變換下只進行“規則”變換的向量，這個“規則”就是特徵值。推薦教材linear algebra and its application
這幾個方向上線性變換只導致伸縮，沒有旋轉；特徵值反映線性變換在這幾個方向上導致的伸縮的大小。
定義很抽象我也一直搞不懂，但是最近開始在圖像處理方面具體應用的時候就清晰很多了，用學渣的語言溝通一下吧我們。
拋開學術研究不談，其實根本不會，特徵值eigenvalue和特徵向量eigenvector的一大應用是用於大量數據的降維
比如拿淘寶舉個例子，每個淘寶店鋪有N個統計數據：商品類型，日銷量周銷量月銷量、好評率中評差評率……全淘寶有M家店鋪，那麼服務器需要記錄的數據就是M＊N的矩陣；
這是一個很大的數據，實際上我們可以通過求這個矩陣的特徵向量和對應的特徵值來重新表示這個M＊N的矩陣：
我們可以用周銷量來誤差不大的表示日銷量和月銷量（除以七和乘以四），這個時候周銷量就可以當作一個特徵向量，它能夠表示每個店鋪銷量這個空間方向的主要能量（也就是數據），這樣我們就簡略的把一個35維的向量簡化成四維的（30個日銷量加4個周銷量加1個月銷量）；
同理我們也可以把好評率中評率差評率用一個好評率來表示（剩餘的百分比默認為差評率），這樣的降維大致上也能反映一個店鋪的誠信度；
這樣通過不斷的降維我們可以提取到某系列數據最主要的幾個特徵向量（對應特徵值最大的），這些向量反映了這個矩陣空間最主要的能量分佈，所以我們可以用這幾個特徵向量來表示整個空間，實現空間的降維。
這
僅考慮非奇異矩陣。
以3階非奇異矩陣
為例，設它的3個特徵值（多重特徵值就重複寫）分別為
,
,
, 對應的特徵向量分別為
,
和
，則
線性無關。此時任一向量
可表示為
的線性組合，設
,則有
正好是
在
的各特徵向量上分量乘以特徵值之和。