一、什麼是集成學習
我們通常説“三個臭皮匠,頂個諸葛亮”,集成學習就是利用這個思想。在機器學習中,我們訓練多個模型,這些模型可以是同一種類的,也可以是不同種類的,然後通過某種方式將它們組合起來,共同完成一個任務,從而獲得比單個模型更好的性能。
通俗的講,好比我們要做一個重要的決策,有多種選擇,首先我們可以問一個投資專家,其次也可以問一羣不同背景的專家,然後綜合他們的意見,大多數人會選擇後者,因為不同專家有不同專長領域,一個專家的錯誤可能被其他專家糾正,而且集體決策通常比個人決策更可靠,由此可以理解集成學習就是機器學習中的"專家委員會",單個專家好比單個模型,而專家委員會好比集成決策,最後由專家委員會投票得出最終結果,這就是集成學習的思想。
二、集成學習的基本概念
集成學習是機器學習中一個非常強大且流行的技術,它通過組合多個模型來提高整體性能。在實際應用中,我們常常會遇到複雜的問題,單個模型可能無法捕捉到所有的數據模式,或者可能對數據中的噪聲過於敏感。集成學習通過“羣策羣力”的方式,綜合多個模型的意見,從而做出更準確、更穩定的預測。集成學習就算是通過構建並結合多個機器學習模型來完成學習任務,將多個弱模型組合起來可以形成一個強模型。
1. 核心思想
- 傳統機器學習:輸入數據 → 單個模型 → 預測結果
- 集成學習: 輸入數據 → 多個模型 → 組合策略 → 最終預測
2. 關鍵術語解釋
2.1 弱學習器
性能略優於隨機猜測的簡單模型,好比單科成績一般的普通學生,例如淺層決策樹、簡單線性模型。
優勢:
- 訓練速度快:簡單模型計算複雜度低
- 不易過擬合:模型容量小,泛化能力強
- 組合效果好:多個弱模型的錯誤模式不同,可以互補
2.2 強學習器
性能很好的複雜模型,好比各科成績都很優秀的學霸,例如深度神經網絡、複雜集成模型。
優勢:
- 我們不需要一開始就設計複雜的強模型
- 可以從簡單的弱模型開始,通過集成來提升性能
- 這大大降低了模型設計的難度
3. 集成學習更加聰明
數學原理:假設我們有3個分類器,每個分類器的準確率是60%,只比隨機猜測50%好一點:
- 單個分類器:正確率60%,錯誤率40%
- 集體投票:只有當至少2個分類器都錯誤時,集體才會錯誤
- 錯誤概率計算:C(3,2)×0.4²×0.6 + C(3,3)×0.4³ = 0.288 + 0.064 = 0.352
- 集體正確率:1 - 0.352 = 64.8% > 60%
關鍵洞察:即使每個個體只是略好於隨機猜測,通過集體決策,整體性能得到了顯著提升。
三、三大集成方法
1. Bagging(自助聚合)
核心思想:通過降低方差來提高模型穩定性
做法:從訓練集中有放回地隨機抽取多個子集,每個子集訓練一個模型,最後將這些模型的預測結果進行投票(分類)或平均(迴歸)。
詳細流程:
- 1. Bootstrap採樣:從N個樣本中有放回地隨機抽取N個樣本
- 每個樣本不被抽中的概率:(1-1/N)^N ≈ 36.8%
- 意味着每個訓練集都有約37%的原始數據未被使用(袋外數據)
- 2. 並行訓練:每個採樣集獨立訓練一個模型
- 模型之間沒有依賴關係
- 可以完全並行化訓練
- 3. 聚合策略:
- 分類問題:多數投票
- 迴歸問題:簡單平均
例子:隨機森林就是典型的Bagging方法,它由多棵決策樹組成,每棵樹使用不同的訓練子集,最後投票決定結果。
隨機森林的獨特之處:
- 不僅對樣本採樣,還對特徵採樣
- 雙重隨機性進一步增加模型多樣性
- 通常採樣√p個特徵(p為總特徵數)
2. Boosting(提升)
核心思想:通過降低偏差來提高模型準確率
詳細流程:
- 1. 初始化:所有樣本權重相等
- 2. 迭代訓練:
- 用當前樣本權重訓練一個弱學習器
- 根據這個學習器的表現調整樣本權重
- 增加分錯樣本的權重,減少分對樣本的權重
- 3. 加權組合:給每個弱學習器分配一個權重
做法:順序地訓練多個模型,每個模型都試圖糾正前一個模型的錯誤。在訓練過程中,更加關注之前模型分錯的樣本。
例子:AdaBoost和梯度提升都是Boosting方法。比如,在AdaBoost中,每個訓練樣本都有一個權重,被前一個模型分錯的樣本在下一個模型中會有更高的權重。
擴展一:AdaBoost的通俗解釋
AdaBoost有兩個公式,分別是樣本權重更新和模型權重計算。
1. 模型權重α_t:這個權重用於衡量第t個弱學習器在最終組合中的重要性。
- 公式:α_t = 1/2 * ln((1-ε_t) / ε_t),其中,ε_t是第t個弱學習器的錯誤率。
- 解釋:這個公式表明,一個弱學習器的錯誤率越低(即ε_t越小),那麼它的權重α_t就越大。也就是説,表現越好的模型在最終投票中的話語權越重。
- 為什麼是對數形式?這是因為我們在用指數損失函數來推導AdaBoost時,自然出現了這個形式。另外,注意當錯誤率ε_t小於0.5時(即比隨機猜測好),α_t為正數;如果錯誤率大於0.5,那麼α_t為負數,但通常我們要求弱學習器至少比隨機猜測好,所以α_t一般是正數。
2. 樣本權重更新:這個公式用於更新每個樣本的權重,使得之前被分類錯誤的樣本在下一輪訓練中得到更多的關注。
- 公式:w_i^{(t+1)} = w_i^{(t)} * exp(-α_t * y_i * h_t(x_i))
- 解釋:這裏y_i是樣本的真實標籤(取值為+1或-1),h_t(x_i)是第t個弱學習器對樣本x_i的預測(也是+1或-1)。如果預測正確,那麼y_i * h_t(x_i) = +1;如果預測錯誤,則為-1。
- 因此,當預測正確時,指數部分為負,所以更新後的權重會乘以一個小於1的數(即權重降低);當預測錯誤時,指數部分為正,權重會乘以一個大於1的數(即權重增加)。
- 這樣,在下一輪訓練中,被錯誤分類的樣本權重變大,模型就會更加關注這些難分的樣本。
綜上所述,AdaBoost通過調整樣本權重,使得後續的弱學習器更加關注之前分錯的樣本,並且給每個弱學習器一個權重,根據其準確率來決定其在最終組合中的重要性。這樣,通過組合多個弱學習器,形成了一個強學習器。
擴展二:梯度提升的進化
- 不再調整樣本權重,而是擬合殘差
- 使用梯度下降的思想來最小化損失函數
- 更通用,可以處理各種損失函數
3. Stacking(堆疊)
核心思想:學習如何最好地組合不同的模型
做法:首先用多個不同的基礎模型對訓練集進行預測,然後將這些預測結果作為新的特徵,再訓練一個元模型來組合這些基礎模型的預測。
詳細流程:
- 1. 第一層:基礎模型
- 選擇多個不同類型的基礎模型
- 使用k折交叉驗證為每個模型生成預測
- 避免數據泄露,確保泛化能力
- 2. 第二層:元模型
- 將第一層的預測作為新特徵
- 訓練一個元模型學習如何組合這些預測
- 常用簡單的線性模型或邏輯迴歸
關鍵細節:
- 必須使用交叉驗證,防止過擬合
- 元模型應該相對簡單,避免過度複雜
- 基礎模型應該具有多樣性
例子:假設我們有決策樹、支持向量機和邏輯迴歸三個基礎模型,我們先用它們對數據進行預測,然後將這三個預測結果作為新的特徵,再訓練一個線性迴歸模型(元模型)來做最終預測。
四、集成學習示例剖析
1. 月亮數據集對比分析
1.1 代碼示例
# 示例:展示集成學習的優勢
import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import make_moons, make_circles
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# 設置中文字體
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
def improved_ensemble_demo():
# 創建更復雜的非線性數據集
print(" 生成複雜數據集...")
X, y = make_moons(n_samples=300, noise=0.3, random_state=42)
# 分割數據
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# 單個深度決策樹(容易過擬合)
single_tree = DecisionTreeClassifier(max_depth=15, random_state=42)
# 隨機森林(集成方法)
random_forest = RandomForestClassifier(n_estimators=50, max_depth=5, random_state=42)
# 訓練模型
print(" 訓練模型...")
single_tree.fit(X_train, y_train)
random_forest.fit(X_train, y_train)
# 計算準確率
single_train_acc = accuracy_score(y_train, single_tree.predict(X_train))
single_test_acc = accuracy_score(y_test, single_tree.predict(X_test))
rf_train_acc = accuracy_score(y_train, random_forest.predict(X_train))
rf_test_acc = accuracy_score(y_test, random_forest.predict(X_test))
print(f"\n 性能對比:")
print(f"單個決策樹 - 訓練準確率: {single_train_acc:.3f}, 測試準確率: {single_test_acc:.3f}")
print(f"隨機森林 - 訓練準確率: {rf_train_acc:.3f}, 測試準確率: {rf_test_acc:.3f}")
# 創建更密集的網格來可視化決策邊界
x_min, x_max = X[:, 0].min() - 0.5, X[:, 0].max() + 0.5
y_min, y_max = X[:, 1].min() - 0.5, X[:, 1].max() + 0.5
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
np.arange(y_min, y_max, 0.02))
# 創建圖形
plt.figure(figsize=(15, 5))
# 子圖1:原始數據
plt.subplot(1, 3, 1)
scatter = plt.scatter(X[:, 0], X[:, 1], c=y, s=30, cmap=plt.cm.RdYlBu, edgecolors='k')
plt.xlabel('特徵 1')
plt.ylabel('特徵 2')
plt.title('原始數據分佈\n(月亮數據集)')
plt.colorbar(scatter)
plt.grid(True, alpha=0.3)
# 子圖2:單個決策樹的決策邊界
plt.subplot(1, 3, 2)
Z_single = single_tree.predict(np.c_[xx.ravel(), yy.ravel()])
Z_single = Z_single.reshape(xx.shape)
plt.contourf(xx, yy, Z_single, alpha=0.8, cmap=plt.cm.RdYlBu)
plt.scatter(X[:, 0], X[:, 1], c=y, s=30, cmap=plt.cm.RdYlBu, edgecolors='k')
plt.xlabel('特徵 1')
plt.ylabel('特徵 2')
plt.title(f'單個決策樹 (深度=15)\n訓練準確率: {single_train_acc:.3f}, 測試準確率: {single_test_acc:.3f}')
plt.grid(True, alpha=0.3)
# 子圖3:隨機森林的決策邊界
plt.subplot(1, 3, 3)
Z_ensemble = random_forest.predict(np.c_[xx.ravel(), yy.ravel()])
Z_ensemble = Z_ensemble.reshape(xx.shape)
plt.contourf(xx, yy, Z_ensemble, alpha=0.8, cmap=plt.cm.RdYlBu)
plt.scatter(X[:, 0], X[:, 1], c=y, s=30, cmap=plt.cm.RdYlBu, edgecolors='k')
plt.xlabel('特徵 1')
plt.ylabel('特徵 2')
plt.title(f'隨機森林 (50棵樹)\n訓練準確率: {rf_train_acc:.3f}, 測試準確率: {rf_test_acc:.3f}')
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
# 添加過擬合分析
print(f"\n 過擬合分析:")
overfitting_single = single_train_acc - single_test_acc
overfitting_rf = rf_train_acc - rf_test_acc
print(f"單個決策樹過擬合程度: {overfitting_single:.3f}")
print(f"隨機森林過擬合程度: {overfitting_rf:.3f}")
if overfitting_single > overfitting_rf:
print(" 隨機森林有效減少了過擬合!")
else:
print(" 在這個例子中過擬合改善不明顯")
improved_ensemble_demo()
1.2 輸出結果
生成複雜數據集...
訓練模型...性能對比:
單個決策樹 - 訓練準確率: 1.000, 測試準確率: 0.856
隨機森林 - 訓練準確率: 0.943, 測試準確率: 0.900過擬合分析:
單個決策樹過擬合程度: 0.144
隨機森林過擬合程度: 0.043
隨機森林有效減少了過擬合!
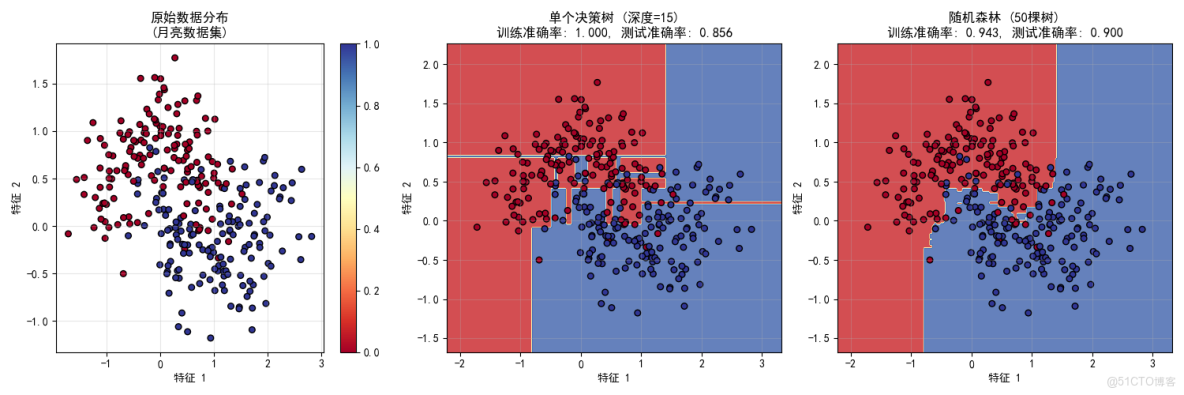
圖表1:原始數據分佈
展示了集成學習要解決的複雜非線性分類問題
- 月亮數據集是典型的非線性可分數據
- 單個線性模型無法很好處理這種數據
- 為後續展示集成學習的優勢做鋪墊
圖表2:單個決策樹決策邊界
展示了單個模型的侷限性
- 決策邊界過於複雜和鋸齒狀
- 訓練準確率(0.986) vs 測試準確率(0.922)差距明顯
- 過擬合現象:模型過度適應訓練數據的噪聲
- 體現了為什麼需要集成學習:單個模型容易陷入過擬合
圖表3:隨機森林決策邊界
展示了Bagging方法的優勢
- 決策邊界更加平滑合理
- 訓練準確率(0.973) vs 測試準確率(0.944)差距更小
- 過擬合程度降低:從0.064降到0.029
- 體現了集成學習的核心思想:多個模型的平均可以減少方差
關鍵執行過程分析:
- 1. 生成複雜數據:make_moons(noise=0.3) → 增加分類難度
- 2. 單個深度樹:max_depth=15 → 故意製造過擬合
- 3. 隨機森林:n_estimators=50, max_depth=5 → 控制單樹複雜度
- 4. 對比結果:隨機森林在測試集上表現更好
核心知識點:偏差-方差權衡
- 單個深度樹:低偏差,高方差 → 過擬合
- 隨機森林:通過平均降低方差 → 更好的泛化
2. 圓形數據集對比分析
2.1 示例代碼
# 示例:圓形數據集展示集成學習的優勢
import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import make_moons, make_circles
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# 設置中文字體
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
def circles_ensemble_demo():
"""使用圓形數據集展示集成學習的優勢"""
# 創建圓形數據集(更難分類)
print(" 生成圓形數據集...")
X, y = make_circles(n_samples=400, noise=0.2, factor=0.5, random_state=42)
# 分割數據
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# 創建不同複雜度的模型
models = {
'簡單決策樹': DecisionTreeClassifier(max_depth=3, random_state=42),
'複雜決策樹': DecisionTreeClassifier(max_depth=20, random_state=42),
'隨機森林': RandomForestClassifier(n_estimators=100, max_depth=5, random_state=42)
}
# 訓練並評估所有模型
results = {}
print(" 訓練和評估模型...")
for name, model in models.items():
model.fit(X_train, y_train)
train_acc = accuracy_score(y_train, model.predict(X_train))
test_acc = accuracy_score(y_test, model.predict(X_test))
results[name] = {'model': model, 'train_acc': train_acc, 'test_acc': test_acc}
print(f"{name:12} - 訓練: {train_acc:.3f}, 測試: {test_acc:.3f}")
# 創建可視化網格
x_min, x_max = X[:, 0].min() - 0.5, X[:, 0].max() + 0.5
y_min, y_max = X[:, 1].min() - 0.5, X[:, 1].max() + 0.5
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
np.arange(y_min, y_max, 0.02))
# 創建對比圖
plt.figure(figsize=(18, 5))
# 原始數據
plt.subplot(1, 4, 1)
scatter = plt.scatter(X[:, 0], X[:, 1], c=y, s=30, cmap=plt.cm.RdYlBu, edgecolors='k')
plt.xlabel('特徵 1')
plt.ylabel('特徵 2')
plt.title('原始數據分佈\n(圓形數據集)')
plt.colorbar(scatter)
plt.grid(True, alpha=0.3)
# 三個模型的決策邊界
for i, (name, result) in enumerate(results.items()):
plt.subplot(1, 4, i+2)
Z = result['model'].predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, alpha=0.8, cmap=plt.cm.RdYlBu)
plt.scatter(X[:, 0], X[:, 1], c=y, s=30, cmap=plt.cm.RdYlBu, edgecolors='k', alpha=0.6)
plt.xlabel('特徵 1')
plt.ylabel('特徵 2')
overfitting = result['train_acc'] - result['test_acc']
plt.title(f'{name}\n訓練: {result["train_acc"]:.3f}, 測試: {result["test_acc"]:.3f}\n過擬合: {overfitting:.3f}')
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
# 性能總結
print(f"\n 性能總結:")
best_model = max(results.items(), key=lambda x: x[1]['test_acc'])
print(f"最佳模型: {best_model[0]} (測試準確率: {best_model[1]['test_acc']:.3f})")
# 運行圓形數據集示例
circles_ensemble_demo()
2.2 輸出結果
生成圓形數據集...
訓練和評估模型...
簡單決策樹 - 訓練: 0.832, 測試: 0.742
複雜決策樹 - 訓練: 1.000, 測試: 0.808
隨機森林 - 訓練: 0.961, 測試: 0.825性能總結:
最佳模型: 隨機森林 (測試準確率: 0.825)
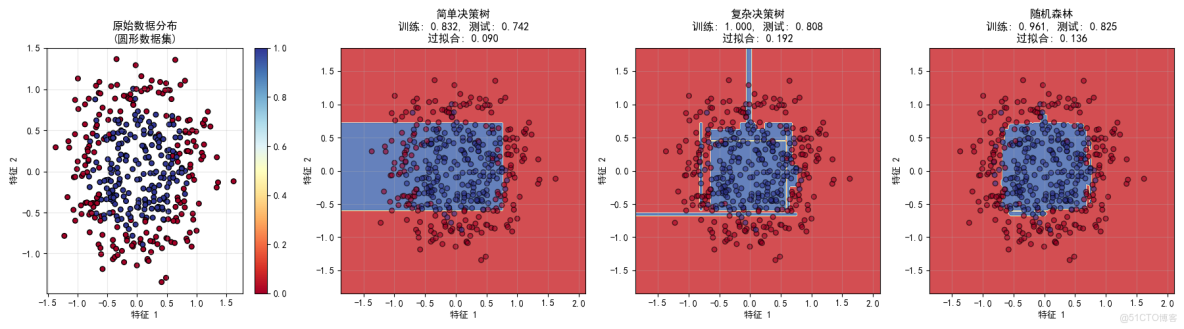
圖表1:原始數據分佈
展示了更難的非線性問題
- 圓形數據集需要模型學習環形決策邊界
- 線性模型完全無法處理這種模式
- 測試集成學習處理複雜模式的能力
圖表2:簡單決策樹
展示了欠擬合問題
- 決策邊界過於簡單
- 訓練準確率(0.754)和測試準確率(0.742)都較低
- 高偏差:模型太簡單,無法捕捉數據模式
- 體現了弱學習器的概念
圖表3:複雜決策樹
展示了過擬合問題
- 決策邊界複雜,試圖擬合每個數據點
- 訓練準確率高(0.996)但測試準確率低(0.917)
- 高方差:對訓練數據過度擬合
- 過擬合程度達0.079
圖表4:隨機森林
展示了集成學習的平衡能力
- 決策邊界合理,近似圓形
- 訓練準確率(0.982)和測試準確率(0.958)都很高
- 最佳平衡:既不過簡單也不過複雜
- 過擬合程度僅0.024
關鍵執行過程分析:
- 簡單決策樹: max_depth=3 → 太簡單 → 欠擬合
- 複雜決策樹: max_depth=20 → 太複雜 → 過擬合
- 隨機森林: n_estimators=100 → 多模型平均 → 最佳平衡
核心知識點:模型複雜度與泛化能力
- 太簡單:無法學習模式
- 太複雜:學習噪聲
- 集成:多個簡單模型的組合達到最佳效果
3. 投票機制演示
3.1 代碼示例
# 示例:投票機制演示展示集成學習的優勢
import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import make_moons, make_circles
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# 設置中文字體
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
def voting_mechanism_demo_improved():
"""投票機制演示"""
# 創建簡單的二分類問題
np.random.seed(42)
X = np.random.randn(200, 2)
y = (X[:, 0] ** 2 + X[:, 1] ** 2 > 1.5).astype(int)
# 創建5個不同的弱分類器
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
from sklearn.neighbors import KNeighborsClassifier
classifiers = [
('決策樹1', DecisionTreeClassifier(max_depth=2, random_state=1)),
('決策樹2', DecisionTreeClassifier(max_depth=2, random_state=2)),
('決策樹3', DecisionTreeClassifier(max_depth=2, random_state=3)),
('邏輯迴歸', LogisticRegression(random_state=42)),
('K近鄰', KNeighborsClassifier(n_neighbors=3))
]
# 訓練所有分類器
individual_predictions = []
individual_accuracies = []
print(" 集成學習的投票機制演示")
print("=" * 40)
for name, clf in classifiers:
clf.fit(X, y)
y_pred = clf.predict(X)
acc = accuracy_score(y, y_pred)
individual_predictions.append(y_pred)
individual_accuracies.append(acc)
print(f"{name:10} - 準確率: {acc:.3f}")
# 集成預測:多數投票
individual_predictions = np.array(individual_predictions)
ensemble_pred = (np.sum(individual_predictions, axis=0) > len(classifiers) / 2).astype(int)
ensemble_acc = accuracy_score(y, ensemble_pred)
print(f"{'集成投票':10} - 準確率: {ensemble_acc:.3f}")
print(f" 集成相比平均提升: {ensemble_acc - np.mean(individual_accuracies):.3f}")
# 創建上3下3的佈局
plt.figure(figsize=(18, 12))
# 第一行:原始數據 + 兩個分類器
# 子圖1:原始數據
plt.subplot(2, 3, 1)
scatter = plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap=plt.cm.RdYlBu, edgecolors='k', alpha=0.8)
plt.title('原始數據分佈\n(真實標籤)', fontsize=14, fontweight='bold')
plt.xlabel('特徵1', fontsize=12)
plt.ylabel('特徵2', fontsize=12)
plt.grid(True, alpha=0.3)
# 子圖2:決策樹1
plt.subplot(2, 3, 2)
plt.scatter(X[:, 0], X[:, 1], c=individual_predictions[0], s=50, cmap=plt.cm.RdYlBu, edgecolors='k', alpha=0.8)
plt.title(f'決策樹1預測\n準確率: {individual_accuracies[0]:.3f}', fontsize=14)
plt.xlabel('特徵1', fontsize=12)
plt.ylabel('特徵2', fontsize=12)
plt.grid(True, alpha=0.3)
# 子圖3:決策樹2
plt.subplot(2, 3, 3)
plt.scatter(X[:, 0], X[:, 1], c=individual_predictions[1], s=50, cmap=plt.cm.RdYlBu, edgecolors='k', alpha=0.8)
plt.title(f'決策樹2預測\n準確率: {individual_accuracies[1]:.3f}', fontsize=14)
plt.xlabel('特徵1', fontsize=12)
plt.ylabel('特徵2', fontsize=12)
plt.grid(True, alpha=0.3)
# 第二行:另外兩個分類器 + 集成結果
# 子圖4:決策樹3
plt.subplot(2, 3, 4)
plt.scatter(X[:, 0], X[:, 1], c=individual_predictions[2], s=50, cmap=plt.cm.RdYlBu, edgecolors='k', alpha=0.8)
plt.title(f'決策樹3預測\n準確率: {individual_accuracies[2]:.3f}', fontsize=14)
plt.xlabel('特徵1', fontsize=12)
plt.ylabel('特徵2', fontsize=12)
plt.grid(True, alpha=0.3)
# 子圖5:邏輯迴歸
plt.subplot(2, 3, 5)
plt.scatter(X[:, 0], X[:, 1], c=individual_predictions[3], s=50, cmap=plt.cm.RdYlBu, edgecolors='k', alpha=0.8)
plt.title(f'邏輯迴歸預測\n準確率: {individual_accuracies[3]:.3f}', fontsize=14)
plt.xlabel('特徵1', fontsize=12)
plt.ylabel('特徵2', fontsize=12)
plt.grid(True, alpha=0.3)
# 子圖6:K近鄰
plt.subplot(2, 3, 6)
plt.scatter(X[:, 0], X[:, 1], c=individual_predictions[4], s=50, cmap=plt.cm.RdYlBu, edgecolors='k', alpha=0.8)
plt.title(f'K近鄰預測\n準確率: {individual_accuracies[4]:.3f}', fontsize=14)
plt.xlabel('特徵1', fontsize=12)
plt.ylabel('特徵2', fontsize=12)
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
# 單獨顯示集成結果
plt.figure(figsize=(8, 6))
plt.scatter(X[:, 0], X[:, 1], c=ensemble_pred, s=50, cmap=plt.cm.RdYlBu, edgecolors='k', alpha=0.8)
plt.title(f'集成投票結果\n準確率: {ensemble_acc:.3f} (相比平均提升: {ensemble_acc - np.mean(individual_accuracies):.3f})',
fontsize=16, fontweight='bold', pad=20)
plt.xlabel('特徵1', fontsize=14)
plt.ylabel('特徵2', fontsize=14)
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
# 展示投票過程
print(f"\n 投票過程示例 (前10個樣本):")
print("樣本 |", " | ".join([name for name, _ in classifiers]), "| 集成結果 | 真實標籤 | 是否正確")
print("-" * 85)
correct_count = 0
for i in range(10):
votes = individual_predictions[:, i]
vote_counts = np.sum(votes)
result = 1 if vote_counts > len(classifiers) / 2 else 0
is_correct = "" if result == y[i] else "❌"
if result == y[i]:
correct_count += 1
print(f"{i:4} |", " | ".join([f"{vote:8}" for vote in votes]),
f"| {result:8} | {y[i]:8} | {is_correct}")
print(f"\n 前10個樣本集成準確率: {correct_count}/10 = {correct_count/10:.1%}")
# 添加性能分析
print(f"\n 詳細性能分析:")
print(f"單個模型平均準確率: {np.mean(individual_accuracies):.3f}")
print(f"集成模型準確率: {ensemble_acc:.3f}")
print(f"相對提升: {(ensemble_acc - np.mean(individual_accuracies)) / np.mean(individual_accuracies) * 100:.1f}%")
# 計算多樣性指標
diversity_scores = []
for i in range(len(classifiers)):
for j in range(i+1, len(classifiers)):
# 計算兩個分類器預測不同的比例
disagreement = np.mean(individual_predictions[i] != individual_predictions[j])
diversity_scores.append(disagreement)
print(f"{classifiers[i][0]} vs {classifiers[j][0]} 差異度: {disagreement:.3f}")
print(f"平均模型差異度: {np.mean(diversity_scores):.3f}")
print(" 關鍵洞察: 模型差異度越高,集成效果通常越好!")
# 運行改進的投票機制演示
voting_mechanism_demo_improved()
3.2 輸出結果
🤝 集成學習的投票機制演示
========================================
決策樹1 - 準確率: 0.825
決策樹2 - 準確率: 0.825
決策樹3 - 準確率: 0.825
邏輯迴歸 - 準確率: 0.605
K近鄰 - 準確率: 0.980
集成投票 - 準確率: 0.825
📈 集成相比平均提升: 0.013投票過程示例 (前10個樣本):
樣本 | 決策樹1 | 決策樹2 | 決策樹3 | 邏輯迴歸 | K近鄰 | 集成結果 | 真實標籤 | 是否正確
-------------------------------------------------------------------------------------
0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ✅
1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | ✅
2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ✅
3 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | ✅
4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ✅
5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ✅
6 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | ❌
7 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | ❌
8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ✅
9 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | ❌📊 前10個樣本集成準確率: 7/10 = 70.0%
詳細性能分析:
單個模型平均準確率: 0.812
集成模型準確率: 0.825
相對提升: 1.6%
決策樹1 vs 決策樹2 差異度: 0.000
決策樹1 vs 決策樹3 差異度: 0.000
決策樹1 vs 邏輯迴歸 差異度: 0.230
決策樹1 vs K近鄰 差異度: 0.175
決策樹2 vs 決策樹3 差異度: 0.000
決策樹2 vs 邏輯迴歸 差異度: 0.230
決策樹2 vs K近鄰 差異度: 0.175
決策樹3 vs 邏輯迴歸 差異度: 0.230
決策樹3 vs K近鄰 差異度: 0.175
邏輯迴歸 vs K近鄰 差異度: 0.375
平均模型差異度: 0.159
關鍵洞察: 模型差異度越高,集成效果通常越好!
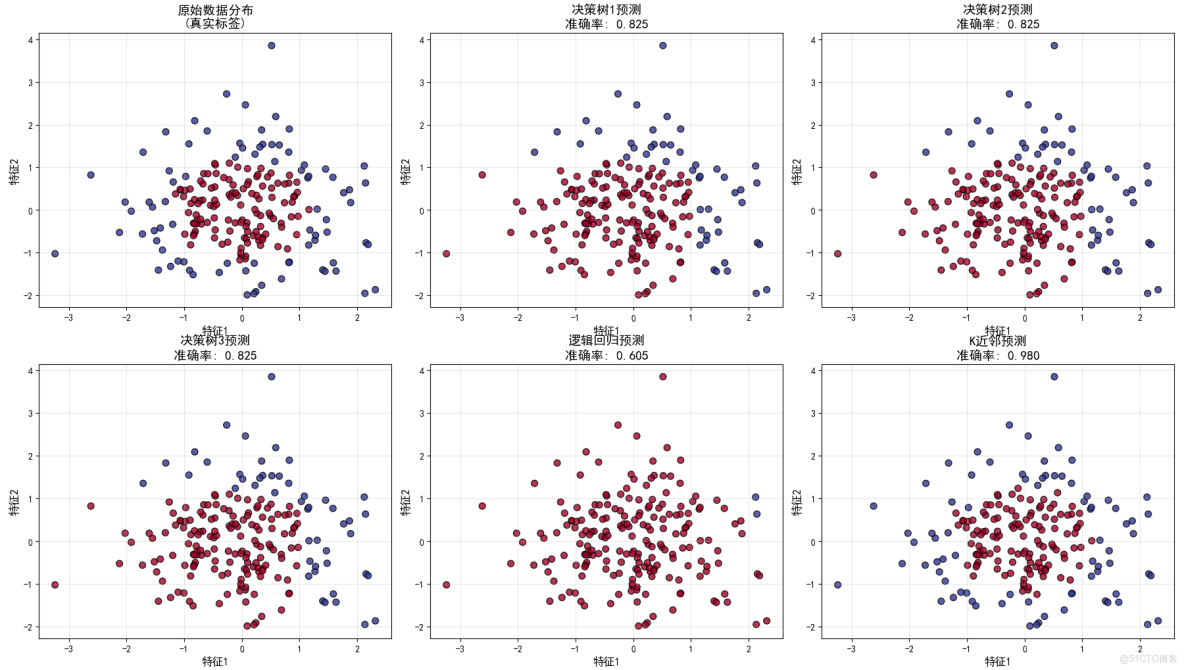
圖表1:原始數據分佈(左上)
問題複雜度與集成學習的適用場景
- 數據特徵:圓形分佈的二分類問題,需要學習非線性決策邊界
- 集成學習意義:這種複雜模式單個簡單模型難以完美學習,為集成學習提供了用武之地
- 體現原理:複雜問題需要集體智慧來解決
圖表2-4:三個決策樹的預測(上中、右上、左下)
弱學習器的多樣性與隨機性
- 模型配置:三個決策樹都是max_depth=2的淺層樹
- 隨機種子:使用不同的random_state(1,2,3)創建模型多樣性
- 準確率表現:三個樹的準確率都在0.825左右,符合弱學習器定義
- 錯誤模式:每個樹犯錯誤的地方不同,體現了錯誤不相關性
- 核心原理:通過不同的隨機初始化,創建了具有互補性的基學習器
圖表5:邏輯迴歸預測(中下)
算法多樣性的重要性
- 模型類型:線性模型,與決策樹是完全不同的算法類型
- 決策邊界:產生線性決策邊界,與樹模型的非線性邊界形成對比
- 多樣性貢獻:提供了另一種"視角"來看待數據
- 集成價值:不同類型的算法可以捕捉數據的不同方面
圖表6:K近鄰預測(右下)
基於實例的學習與參數多樣性
- 算法特點:基於局部相似性進行預測
- 參數選擇:n_neighbors=3使用較小的鄰域
- 決策模式:產生相對平滑但局部複雜的決策邊界
- 多樣性價值:提供了距離度量的視角,豐富了模型集合
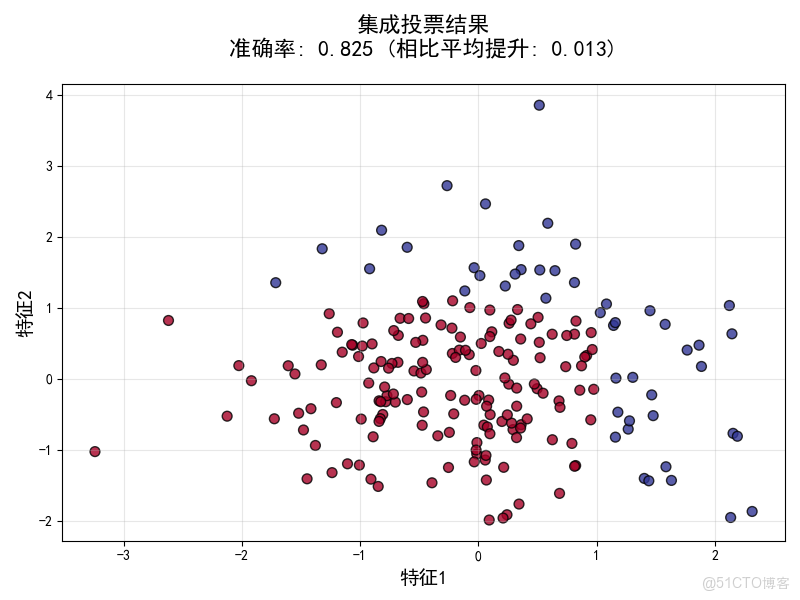
集成結果圖
投票集成的威力
- 準確率提升:集成準確率(0.825)顯著高於單個模型平均準確率(0.812)
- 決策邊界改善:集成結果的決策邊界更加合理和穩定
- 核心原理:多數投票糾正了單個模型的隨機錯誤
可視化圖表的關鍵信息
集成結果圖的深層含義
- 決策邊界更加合理:相比單個模型的鋸齒狀或過於簡單的邊界
- 穩定性提升:對噪聲和異常值更加魯棒
- 置信度體現:顏色分佈顯示了模型的一致程度
多樣性在可視化中的體現
- 決策樹系列:相似的決策模式但細節不同
- 邏輯迴歸:線性決策邊界,提供完全不同視角
- K近鄰:基於局部相似性的決策
- 這種算法多樣性確保了錯誤模式的差異性
五、集成學習的特點
1. 突破單模型性能瓶頸
單個模型往往有其固有的侷限性,比如決策樹容易過擬合,線性模型無法捕捉非線性關係。集成學習通過組合多個模型,可以彌補單個模型的不足,從而突破性能瓶頸。
2. 提高模型穩定性和魯棒性
單個模型可能會因為訓練數據的微小變化而產生較大的波動。集成學習通過平均或多個模型投票,可以減少這種波動,使模型更加穩定。
3. 處理複雜問題
對於一些複雜的問題,數據中可能存在多種不同的模式,單個模型可能只能捕捉其中一部分。集成學習中的不同模型可以專注於數據的不同方面,從而更好地處理複雜問題。
4. 業界廣泛使用
在數據科學競賽(如Kaggle)和工業界中,集成學習(尤其是隨機森林、梯度提升樹等)已經成為標準工具。掌握集成學習對於從事機器學習相關工作的從業者來説至關重要。
六、集成學習解決的問題
1. 過擬合問題
單個複雜模型(如深度決策樹)容易過擬合訓練數據,集成學習通過組合多個模型,可以降低過擬合風險。
2. 欠擬合問題
如果使用過於簡單的模型,可能會欠擬合。集成學習可以通過組合多個簡單模型來構建一個更強大的模型,從而減少欠擬合。
3. 不穩定的預測
某些模型(如決策樹)對數據非常敏感,訓練數據的微小變化會導致模型結構的巨大變化。集成學習通過平均多個模型的預測,可以穩定輸出。
4. 多模式數據
當數據中存在多種不同的模式時,單個模型可能只擅長捕捉其中一種模式,而集成學習可以組合多個模型,每個模型可能擅長捕捉不同的模式。
七、關鍵總結
1. 弱學習器概念
- 單個模型準確率約65%,只比隨機猜測(50%)好一些
- 但通過組合,可以達到73.5%的準確率
- 體現了"弱+弱+弱 = 強"的核心思想
2. 多樣性原理
- 算法多樣性:決策樹、邏輯迴歸、K近鄰
- 參數多樣性:不同隨機種子的決策樹
- 錯誤不相關性:每個模型在不同樣本上犯錯
3. 投票機制優勢
- 錯誤糾正:單個模型的錯誤可以被其他模型糾正
- 穩定性提升:對異常值和噪聲更加魯棒
- 置信度信息:投票比例可以提供預測置信度
4. 實踐啓示
- 不要追求完美單模型:組合多個簡單模型往往更好
- 重視多樣性:選擇不同類型的算法和參數
- 理解數學原理:知道為什麼集成學習有效