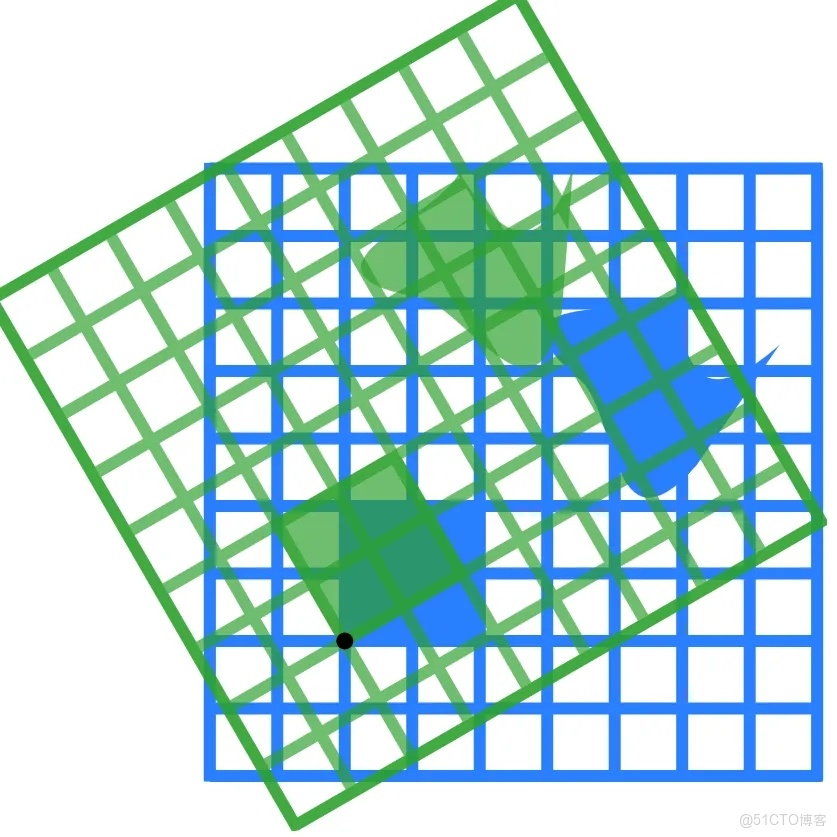
在現代數學的研究中，線性代數佔據着核心位置，它不僅是純數學的重要組成部分，也是物理學、工程學、計算機科學等學科的基礎工具。矩陣與線性變換作為線性代數的核心概念，具有深厚的理論內涵和廣泛的應用價值。矩陣的排列和運算規則表面上似乎只是數字的組合，但其內在體現的是對向量空間結構的精確描述；而線性變換則揭示了向量空間中元素之間的映射規律，是代數與幾何之間的直接聯繫。

理解矩陣與線性變換的關係，不僅僅是掌握一種數學技巧，更是洞察結構、解析規律和揭示系統行為的途徑。在高維空間、複雜系統以及現代科學計算中，線性變換提供了一種統一的框架，讓我們能夠在抽象的空間中操作向量、處理數據、分析系統動態。

然而，矩陣與線性變換的本質並非僅靠公式堆疊可以完全理解。一個矩陣如何對應到具體的變換？為什麼矩陣乘法能夠反映變換的複合？特徵向量和特徵值的意義是什麼？這些問題不僅涉及數學本身，也涉及如何利用線性代數工具去理解自然現象和工程問題。對這些問題的深入思考，將為我們展開系統性的分析提供引導，使我們從代數的角度掌握空間結構和變換規律，同時為後續的高維應用和計算實踐提供基礎。

1 矩陣的基本定義與代數屬性

矩陣是一個按照行和列排列的數字表格，通常記作 ，其中 表示行數， 表示列數，矩陣的每一個元素記作 ，代表矩陣第 行第 列的數值：

矩陣不僅僅是數字的排列，它定義了多種運算，這些運算體現了線性代數的代數結構特徵：

1. 矩陣加法：對於同型矩陣 ，定義

該運算滿足交換律與結合律：

2. 數乘：對於標量 與矩陣 ，定義

數乘與加法結合滿足分配律：

3. 矩陣乘法：矩陣乘法是矩陣最重要的運算之一，定義為

矩陣乘法對應線性變換的複合操作，因此其非交換性具有自然解釋：複合變換的順序決定了最後映射結果。

4. 轉置矩陣：矩陣 的轉置記作 ，定義為

轉置矩陣將行列對調，它在內積、正交性和對稱矩陣分析中起核心作用。

5. 逆矩陣：若 ，有矩陣 使得
   
   其中 是 的單位矩陣。逆矩陣在解線性方程組、求矩陣函數和分析變換可逆性中具有重要價值。
6. 行列式：對於方陣 ，行列式 描述了矩陣映射在體積上的縮放因子：
   
   其中 是 階排列羣， 是排列符號。行列式的非零與矩陣可逆性直接相關。

矩陣的這些基本運算不僅構成了代數系統，而且為矩陣與線性變換的緊密聯繫提供了技術基礎。矩陣的加法與數乘定義了向量空間結構，矩陣乘法對應映射覆合，而轉置、行列式與逆矩陣揭示了結構特徵與映射性質。

2 線性變換的抽象內涵

線性變換是向量空間 到 之間的映射 ，滿足線性條件：

這一定義強調了兩個核心性質：加法保持性與數乘保持性。線性變換使得向量的線性組合在映射下保持結構不變，這是代數與幾何之間的連接。

設 是 維向量空間， 是 維向量空間。如果 是 的一組基， 是 的一組基，那麼線性變換 在這些基下可以表示為矩陣 ：

對任意 ，若 ，則有

其中 。

這一表示顯示了矩陣與線性變換的直接對應關係：矩陣是線性變換在給定基下的座標化形式。不同基選擇會改變矩陣形式，但線性變換本質不變。

線性變換的另一個重要概念是核與像：

• 核（null space）：
  
  核描述了所有被映射到零向量的輸入向量，是衡量映射“丟失信息程度”的指標。
• 像（range）：
  
  像描述了映射能夠覆蓋的空間區域，是映射作用範圍的代數描述。

線性變換的秩-零化度定理（Rank-Nullity Theorem）指出：

它揭示了輸入維度、核維度和像維度之間的固定關係，是線性代數中最基礎而重要的定理之一。

通過以上公式與概念，我們看到線性變換不僅是向量空間間的映射，更具有嚴格的代數結構和可量化特性。這為後續討論矩陣分解、特徵值分析、以及高維數據處理提供了理論基礎。

3 線性變換的抽象內涵

在線性代數中，線性變換是一個向量空間到另一個向量空間之間的映射 ，滿足線性性條件：

這一定義並不依賴於矩陣，線性性意味着結構的保持：加法結構與數量乘法結構在映射下不會被破壞。這正是線性代數中核心的思想。

矩陣與線性變換的關係究竟是什麼？答案是：矩陣是線性變換在特定基下的表示方式。換句話説，矩陣不是線性變換本身，而是線性變換的座標化描述。當我們選擇不同的基，矩陣的形式會發生改變，但其所代表的線性變換本質保持不變。這就解釋了為什麼“同一線性變換”在不同基下會有不同的矩陣表達，而矩陣之間通過相似變換相聯繫。

4 矩陣與線性變換的對應關係

設 是一個 維向量空間， 是一個 維向量空間。如果 是一個線性變換，那麼在選定基 和 之後，我們就可以用矩陣 來表示 ，其關係為：

對於任意 ，若其在基 下的座標是 ，則 的座標為 。

因此我們看到，矩陣並非是孤立的符號，而是與向量空間、基、映射密切聯繫的代數工具。這一對應關係也意味着線性代數的一個核心思想：矩陣化即座標化。

如果我們不依賴於基，線性變換還能如何描述？此時範疇論的視角提供了更高層次的答案：線性變換是向量空間範疇中的態射，而矩陣是這種態射在特定選擇下的實現。

5 線性變換的幾何意義

在線性空間中，線性變換不僅僅是代數對象，還具有幾何作用。例如：

• 在二維空間中，旋轉、伸縮、反射、剪切等幾何操作，都可以由矩陣表示。
• 在三維空間中，投影、座標變換、旋轉等操作，也都是矩陣與線性變換的自然語言。

一個值得注意的點是：幾何意義揭示了代數運算的直觀效果。比如矩陣的行列式與線性變換的體積縮放因子相對應，而行列式的符號則體現了方向是否保持。

幾何直觀是否是理解線性代數的必要條件？從歷史與教學經驗來看，代數形式提供了嚴謹的推理框架，而幾何直觀則幫助我們認識這些形式背後的實際含義。二者相輔相成，缺一不可。

6 特徵值與特徵向量

特徵值與特徵向量是矩陣與線性變換研究中最重要的主題之一。設 是一個線性變換，如果有非零向量 和標量 ，使得：

那麼 稱為特徵值， 稱為特徵向量。

幾何上，特徵向量的方向在變換中保持不變，而特徵值則代表在該方向上的伸縮因子。代數上，特徵值與特徵向量是理解矩陣對角化、譜分解、相似變換等理論的核心。

為什麼特徵值與特徵向量如此重要？其原因在於，若一個矩陣可以被對角化，那麼對其高次冪或函數運算就能大大簡化。例如， 的計算在對角化後變得非常直接。這對於微分方程求解、量子力學算符研究、數值計算等領域都具有極大意義。

7 矩陣分解與計算方法

矩陣分解是理解線性變換的另一關鍵角度。常見分解包括：

• LU 分解：將矩陣分解為下三角矩陣與上三角矩陣的乘積，用於解線性方程組。
• QR 分解：分解為正交矩陣與上三角矩陣，應用於數值穩定性。
• SVD 分解：奇異值分解將任意矩陣分解為 ，其幾何意義是伸縮與旋轉的組合。

SVD 在信息科學中有極為廣泛的應用，如數據壓縮、主成分分析、機器學習中的特徵提取等。

矩陣分解是否只是計算技巧？答案是否定的。矩陣分解揭示了線性變換的本質結構，它將複雜的映射分解為基本的旋轉、伸縮與投影操作，從而讓我們能夠從根本上把握其規律。

8 高維空間中的線性變換

當維度升高時，線性變換的複雜性迅速增長。二維與三維空間中的直觀幾何圖像難以延伸至高維空間，但代數形式依然有效。矩陣提供了一種在任意維度中描述變換的普適工具。

例如，在數據科學中，一個樣本點常常是高維向量。主成分分析的過程，本質上就是尋找一組新的基，使得數據在這些方向上的方差最大，而這正是線性變換與特徵值問題的自然應用。

是否可以僅依靠代數工具，而完全脱離幾何直觀來理解高維空間？答案是肯定的，但在某些情況下，藉助投影與可視化方法，人類的直覺仍然發揮着重要作用。

9 矩陣與線性變換在科學中的作用

矩陣與線性變換不僅僅是純數學的研究對象，它們在科學與技術中有着廣泛的應用：

• 在物理中，量子力學算符就是線性變換，希爾伯特空間中的態向量與矩陣運算緊密相關。
• 在計算機圖形學中，二維與三維圖像的旋轉、縮放、投影，均通過矩陣運算實現。
• 在機器學習中，神經網絡的每一層本質上是線性變換與非線性映射的複合。
• 在信號處理與控制理論中，系統狀態的更新可以用矩陣遞推來描述。

為什麼線性工具如此普適？這是因為線性結構是最基礎、最簡化的數學結構，而許多複雜的非線性問題，可以通過線性化近似在局部得到處理。

10 總結

通過以上討論，我們可以得出結論：

1. 矩陣是線性變換在特定基下的表示，而線性變換是更高層次的抽象對象。
2. 矩陣的代數運算對應於線性變換的複合與運算規律。
3. 幾何意義與代數結構相輔相成，共同揭示了矩陣與線性變換的本質。
4. 特徵值、矩陣分解、高維結構，是深入理解線性代數的核心內容。
5. 矩陣與線性變換在科學與技術中的作用極為廣泛，幾乎貫穿所有現代學科。

然而，是否有更一般的代數對象，能夠進一步推廣矩陣與線性變換的思想？例如，在張量分析、算子代數、範疇論中，矩陣只是更大體系中的一個特例。